
- •Руководство для выполнения контрольной работы по эконометрике
- •Тема 1. Парная регрессия
- •1.1. Линейная парная регрессия
- •1.2. Нелинейная парная регрессия
- •1.2.4 Остаточная сумма квадратов отклонений:
- •1.2.6 Средняя относительная ошибка аппроксимации:
- •1.2.7 Средний коэффициент эластичности:
- •Тема 2. Множественная регрессия
- •Тема 3. Временные ряды
- •Распределение Дарбина-Уотсона
- •Литература
Министерство образования и науки РФ
ГОУ ВПО
Российский государственный торгово-экономический университет
Казанский институт
_______________________________________________________
Кафедра информатики и высшей математики
ТАЛЫЗИН В.А.
Руководство для выполнения контрольной работы по эконометрике
Учебное пособие
КАЗАНЬ-2011г.
Тема 1. Парная регрессия
1.1. Линейная парная регрессия
Расчетные формулы
-
Оценки коэффициентов модели:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
-
Выборочные дисперсии и средние квадратические отклонения:
![]() .
.
-
Выборочный коэффициент парной корреляции:
![]() .
.
-
Средний коэффициент эластичности:
![]() .
.
-
Коэффициент детерминации:
![]() .
.
-
Дисперсионное отношение Фишера (
 -критерий):
-критерий):
![]() .
.
-
Остаточная сумма квадратов отклонений:
![]() .
.
-
Средняя относительная ошибка аппроксимации:
![]() .
.
-
Стандартная ошибка уравнения регрессии:
![]() .
.
-
Стандартные ошибки параметров регрессии:
 .
.
1.11
![]() статистики
Стьюдента параметров уравнения:
статистики
Стьюдента параметров уравнения:
![]() .
.
1.12 Предельные
ошибки коэффициентов уравнения, которые
с вероятностью (1-![]() ),
где
),
где
![]() уровень
значимости, не будут превышены:
уровень
значимости, не будут превышены:
![]() .
.
1.13 Доверительные интервалы для коэффициентов уравнения регрессии:
![]() .
.
1.14 Стандартная
ошибка индивидуального прогнозного
значения
![]() результирующего признака:
результирующего признака:
 .
.
1.15 Доверительный интервал для прогнозного значения:
![]() .
.
Решение типовой задачи.
В таблице 1.1
приводятся данные о заработной плате
(![]() ,
долл.) и возрасте (
,
долл.) и возрасте (![]() ,
лет) по 20 рабочим.
,
лет) по 20 рабочим.
Табл. 1.1
-

300
400
300
320
200
350
350
400
380
400

29
40
36
31
23
45
38
40
50
47
-

250
350
200
400
220
320
390
360
260
250

28
30
25
48
30
40
40
38
29
25
Требуется:
1.
Построить поле корреляции и сформулировать
гипотезу о форме связи
![]() и
и
![]() .
.
2. Построить линейную регрессионную модель зависимости заработной платы от возраста рабочего, вычислить средний коэффициент эластичности, определить коэффициент детерминации и среднюю относительную ошибку аппроксимации и оценить точность модели.
3. Оценить статистическую значимость параметров регрессии и модели в целом, а также построить интервальную оценку коэффициентов линейной регрессии с надежностью 0,95.
4.
Выполнить прогноз заработной платы
![]() для 33-летнего рабочего, оценить точность
прогноза, рассчитав стандартную ошибку
прогноза и его доверительный интервал.
для 33-летнего рабочего, оценить точность
прогноза, рассчитав стандартную ошибку
прогноза и его доверительный интервал.
Решение выполним в среде MS Excel.
-
Сформируем расчетную таблицу следующей структуры:
|
№ п/п |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
Сумма |
|
|
|
|
|
|
|
|
|
|
Среднее |
|
|
|
|
|
|
|
|
|
Введем исходные
данные
![]() ,
,![]() в таблицу по столбцам.
в таблицу по столбцам.
Построим поле корреляции при помощи Мастера диаграмм (тип – Точечная диаграмма) и выполним визуальный анализ типа зависимости.

Поле корреляции
По виду поля
корреляции можно сделать вывод о том,
что форма связи переменных
![]() и
и
![]() может быть как линейной, так и нелинейной.
может быть как линейной, так и нелинейной.
2.
Рассчитаем колонки
![]() ,
,
![]() ,
,
![]() расчетной таблицы. Вычисляем суммы и
средние значения столбцов с помощью
функций СУММ(…)
и
СРЗНАЧ(…).
расчетной таблицы. Вычисляем суммы и
средние значения столбцов с помощью
функций СУММ(…)
и
СРЗНАЧ(…).
Выполним расчет параметров уравнения регрессии по формулам 1.1:
![]() ,
,
![]() .
.
В итоге линейная модель имеет вид:
![]() .
.
Коэффициент
регрессии
![]() показывает, что в среднем заработная
плата растет на
показывает, что в среднем заработная
плата растет на
![]() доллара при увеличении возраста рабочего
на 1 год.
доллара при увеличении возраста рабочего
на 1 год.
Найдем значения выборочных дисперсий и СКО по формулам 1.2:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Определим выборочный
коэффициент корреляции по одной из
формул 1.3:
![]() .
.
Коэффициент парной корреляции по шкале Чеддока является высоким, что свидетельствует о существенной зависимости з/п от возраста рабочего.
Вычислим средний коэффициент эластичности по формуле 1.4:
![]()
![]() .
.
Он показывает, что при увеличении возраста рабочего на 1 % от среднего значения з/п в среднем возрастает на 0,799%.
Рассчитаем коэффициент детерминации по формуле 1.5:
![]() .
.
![]() также близок к
единице и по нему следует, что з/п на 72%
объясняется таким фактором, как возраст
рабочего.
также близок к
единице и по нему следует, что з/п на 72%
объясняется таким фактором, как возраст
рабочего.
Вычислим предсказанные моделью значения з/п по формуле
![]()
и тем самым заполним
колонку
![]() расчетной таблицы. Далее вычисляются
остатки
расчетной таблицы. Далее вычисляются
остатки
![]() и их квадраты
и их квадраты
![]() .
В итоге в строке "Сумма" таблицы
определится остаточная сумма квадратов
.
В итоге в строке "Сумма" таблицы
определится остаточная сумма квадратов
![]() .
.
Проверим качество
модели по средней относительной ошибке
аппроксимации, вычислив
![]() по формуле 1.8. Для этого в первой строке
колонки
по формуле 1.8. Для этого в первой строке
колонки
![]() набираем с использованием функции
ABS(…)
формулу: =ABS(
набираем с использованием функции
ABS(…)
формулу: =ABS(![]() )*100.
После протяжки по всему столбцу вычисляем
среднее значение данного столбца:
)*100.
После протяжки по всему столбцу вычисляем
среднее значение данного столбца:
![]() =
=![]() .
.
По
![]() видно, что в среднем расчетные значения
отклоняются от фактических на 10,2%, что
говорит о допустимом качестве модели
по этому критерию.
видно, что в среднем расчетные значения
отклоняются от фактических на 10,2%, что
говорит о допустимом качестве модели
по этому критерию.
Далее построим график линейной функции на поле корреляции с помощью Мастера диаграмм и убедимся, что МНК дал хорошие результаты аппроксимации.
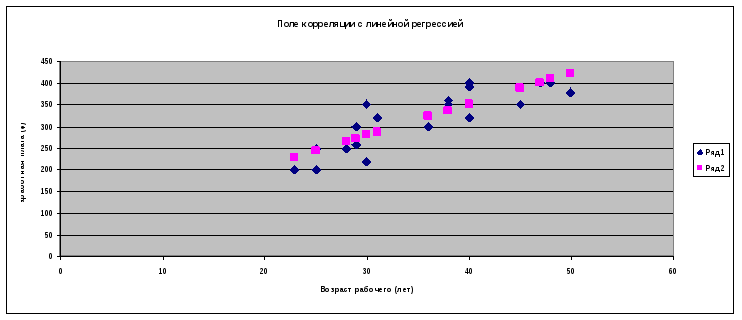
Поле корреляции с линейной регрессией
3. По формулам 1.9 и 1.10 найдем стандартные ошибки уравнения регрессии и его параметров:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Рассчитаем
![]() статистики
Стьюдента по формулам 1.11:
статистики
Стьюдента по формулам 1.11:
![]() ,
,
![]() ,
,
![]() .
.
Обратим внимание
на то, что
![]() ,
а
,
а
![]() .
.
Найдем с помощью
функции СТЬЮДРАСПОБР(…)
табличное значение
![]() по уровню значимости
по уровню значимости
![]() и числу степеней свободы
и числу степеней свободы
![]() .
Сравнение расчетных значений с табличным
.
Сравнение расчетных значений с табличным
![]() указывает на статистическую значимость
параметров
указывает на статистическую значимость
параметров
![]() и
и
![]() .
Параметр же
.
Параметр же
![]() не является значимым, поскольку
не является значимым, поскольку
![]() .
.
Доверительные
интервалы строим только для коэффициентов
модели, точечные оценки которых являются
статистически значимыми. В нашем случае
– только для коэффициента регрессии
![]() :
:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Рассчитаем
![]() критерий
Фишера по формуле 1.6:
критерий
Фишера по формуле 1.6:
![]() .
.
Табличное значение
![]() =
=![]() определяем с помощью встроенной
статистической функции FРАСПОБР
по уровню значимости
определяем с помощью встроенной
статистической функции FРАСПОБР
по уровню значимости
![]() и числам свободы
и числам свободы
![]() и
и
![]() .
Поскольку
.
Поскольку
![]() ,
то можно сделать вывод об адекватности
построенной модели.
,
то можно сделать вывод об адекватности
построенной модели.
4. Получим прогнозную заработную плату для 33-летнего рабочего по найденной линейной модели:
![]() (долл.).
(долл.).
Вычислим стандартную ошибку прогнозного значения по формуле 1.14:
![]() .
.
Находим 95% доверительный интервал для прогнозного значения з/п 33-летнего рабочего с использованием формулы 1.15:
![]() ,
,
![]() .
.
Таким образом, заработная плата 33-летнего рабочего с вероятностью 0,95 находится в пределах от 220,38 до 382,27 долларов.
