3.2.3 Определение уточненных геометрических размеров конической зубчатой передачи

Углы делительных конусов вычисляют по следующим формулам:

для колеса 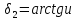(3.5)

для шестерни (3.6)

Определяем уточненные значения делительных диаметров

Выбираем коэффициент смещения режущего инструмента 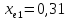(1, стр. 85).

Находим внешние диаметры выступов и впадин:

Определим внешнее конусное расстояние

Ширина зубчатого венца

Внешняя высота зуба

3.2.4 Определение сил в конической зубчатой передаче

Найдем средний делительный диаметр

Тангенциальные силы на шестерне и колесе

Радиальная сила на шестерне

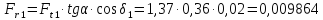
Осевая сила на шестерне

– стандартный угол зацепления

3.2.5 Степень точности передач

Степень точности зависит от окружной скорости зубьев шестерни и колеса.

Окружная скорость определяют по формуле:

где V – окружная скорость, м/с

– угловая скорость колеса,

– средний делительный диаметр колеса, м

Подставляя, получаем

м/с

Согласно таблице 6.5 [1, стр. 73] степень точности передачи равна 8.

3.2.6 Проверка зубьев колес по напряжениям изгиба

Расчетное напряжение изгиба в зубьях колеса определяется по формуле

– расчетное изгибное напряжение в зубьях колеса, МПа

– коэффициент формы зуба колеса [1, стр. 77, таблица 6.9]

– коэффициент неравномерности изгибных напряжений по длине зуба [1, стр. 75, таблица 6.7]

– коэффициент динамичности по изгибным напряжениям [1, стр. 76, таблица 6.8]

– ширина зубчатого венца, мм

– средний нормальный модуль

– коэффициент нагрузочной способности конической передачи по изгибным напряжениям (для прямозубой )

Эквивалентное число зубьев определяются по формуле

Найдем средний нормальный модуль

Подставляя все в формулу, находим напряжение изгиба в зубьях колеса

Расчетное напряжение изгиба в зубьях шестерни проверяем по следующей формуле:

3.2.7 Проверка зубьев колеса по контактным напряжениям

Рассчитаем контактное напряжение

– коэффициент динамичности нагрузки по контактным напряжениям [1, стр. 78]

Список литературы

1. Миронов Е.Н. Курсовое проектирование машин, 2000