- •Расчетно-графическая работа
- •Содержание
- •1 Выбор электродвигателя к механическому приводу общего назначения и кинематический расчет привода
- •Состав, устройство и работа привода
- •1.2 Выбор электродвигателя
- •1.2.1 Расчет необходимой мощности электродвигателя
- •1.2.1.1 Определение мощности на выходном валу привода
- •1.2.1.2 Определение общего кпд привода
- •1.2.2 Расчет частоты вращения вала электродвигателя
- •1.2.2.1 Определения частоты вращения выходного вала привода
- •1.2.2.2 Определение желаемого передаточного числа привода
- •1.3 Кинематический расчет
- •1.3.1 Разбивка передаточного числа по ступеням
- •1.3.2 Кинематические расчеты
- •2.3.2 Расчет допустимых изгибных напряжений
- •3.2.2 Расчет модуля передачи
- •3.2.3 Определение уточненных геометрических размеров конической зубчатой передачи
- •3.2.4 Определение сил в конической зубчатой передаче
- •3.2.5 Степень точности передач
- •3.2.6 Проверка зубьев колес по напряжениям изгиба
- •3.2.7 Проверка зубьев колеса по контактным напряжениям
2.3.2 Расчет допустимых изгибных напряжений
Расчет допустимых изгибных напряжений проводится исходя из тех же предпосылок, что и расчет допустимых контактных напряжений, потому что усталостно-изгибная долговечность (число циклов нагружения до разрушения) имеет аналогичную зависимость от величины изгибных напряжений что и при контактно-усталостном нагружении, поэтому расчет допустимых изгибных напряжений производят по формулам:
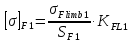 (2.11)
(2.11)
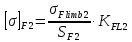 (2.12)
(2.12)
где
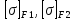 – допускаемые изгибным напряжения для
материала шестерни и колеса соответственно,
Мпа
– допускаемые изгибным напряжения для
материала шестерни и колеса соответственно,
Мпа
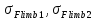 – предельные
значения допускаемых изгибным напряжений,
определяемые по таблице 4.3 [1, стр. 50], для
материала шестерни и колеса соответственно,
Мпа
– предельные
значения допускаемых изгибным напряжений,
определяемые по таблице 4.3 [1, стр. 50], для
материала шестерни и колеса соответственно,
Мпа
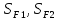 – коэффициенты
безопасности по изгибным напряжениям,
определяемые по таблице 4.3 [1, стр. 50], для
материала шестерни и колеса соответственно
– коэффициенты
безопасности по изгибным напряжениям,
определяемые по таблице 4.3 [1, стр. 50], для
материала шестерни и колеса соответственно
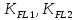 – коэффициенты
долговечности по изгибным напряжениям,
определяемые по формулам (2.13) и (2.14)
– коэффициенты
долговечности по изгибным напряжениям,
определяемые по формулам (2.13) и (2.14)
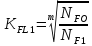 (2.13)
(2.13)
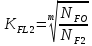 (2.14)
(2.14)
где m – показатель степени. Принимается:
m
= 6 при HB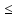 350
350
m
= 9 при HB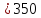
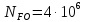 цикл
– базовое количество циклов при
усталостно-изгибном нагружении
цикл
– базовое количество циклов при
усталостно-изгибном нагружении
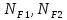 – число
циклов нагружения изгибными нагрузками
шестерни и колеса соответственно, цикл
– число
циклов нагружения изгибными нагрузками
шестерни и колеса соответственно, цикл
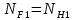 ,
,
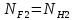 при
при
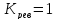
или
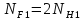 ,
,
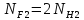 при
при
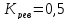
Подставляя значения в формулы, получаем:
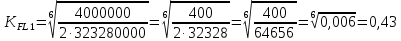
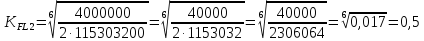
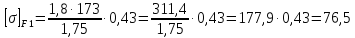 МПа
МПа
 МПа
МПа
3 Проектирование конической зубчатой передачи
3.1 Исходные данные
Для расчета используем данные, полученные в 1-ой и 2-ой частях данной работы
3.2 Этапы расчета конических зубчатых передач
3.2.1 Предварительный диаметр внешней делительной окружности колеса
Проектный расчет конической передачи начинают с определения предварительного значения внешнего делительного диаметра колеса по следующей формуле:
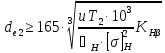 (3.1)
(3.1)
где
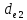 – внешний делительный диаметр конического
зубчатого колеса, мм
– внешний делительный диаметр конического
зубчатого колеса, мм
 – коэффициент
концентрации нагрузки по контактным
напряжениям, определяется по таблице
6.2 [1, стр.67] в зависимости от
– коэффициент
концентрации нагрузки по контактным
напряжениям, определяется по таблице
6.2 [1, стр.67] в зависимости от
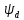 – величины коэффициента ширины зубчатого
колеса по делительному диаметру, который
для конического зацепления может быть
определен по формуле (3.2)
– величины коэффициента ширины зубчатого
колеса по делительному диаметру, который
для конического зацепления может быть
определен по формуле (3.2)
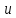 – передаточное
число проектируемой передачи
– передаточное
число проектируемой передачи
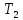 – момент
на валу зубчатого колеса,
– момент
на валу зубчатого колеса,
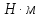
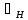 – коэффициент
нагрузочной способности конической
передачи по контактным напряжениям
(для прямозубой -
– коэффициент
нагрузочной способности конической
передачи по контактным напряжениям
(для прямозубой -
 )
)
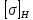 – допустимые
контактные напряжения для зубчатой
передачи, МПа
– допустимые
контактные напряжения для зубчатой
передачи, МПа
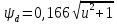 (3.1)
(3.1)
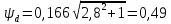
Подставляя все значения в формулу получаем:
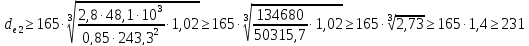
Полученное
значение округляем до ближайшего
значения из ряда нормальных линейных
размеров [1, стр.68, таблица 6.3] и окончательно
принимаем
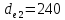 мм.
мм.
3.2.2 Расчет модуля передачи
Определим предварительное значение внешнего диаметра конической зубчатой шестерни
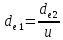 (3.3)
(3.3)
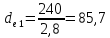
Выбираем
ориентировочное число зубьев шестерни
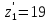 [1, стр.82, таблица 7.2]
[1, стр.82, таблица 7.2]
Определяем число зубьев шестерни по формуле:
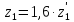 [1,
стр.82, таблица 7.3]
[1,
стр.82, таблица 7.3]
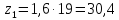
Округляем
до целого числа и получаем
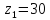
Число зубьев колеса определяем по формуле:
 (3.4)
(3.4)
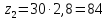
Определим внешний торцовый модуль
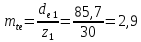
Торцовый
модуль округляем до стандартного
значения [1, стр.69, таблица 6.4] и окончательно
принимаем