-
Производная и дифференциал
-
Сформулируйте определение производной. Каков ее механический и геометрический смысл?
-
Какой класс функций шире: непрерывных или дифференцируемых? Приведите примеры.
-
Выведите формулы производных суммы, произведения, частного двух функций. Приведите примеры.
-
Выведите формулу дифференцирования сложной функции.
-
Запомните таблицу основных формул дифференцирования.
-
Сформулируйте определение дифференциала функции. Каков его геометрический смысл?
-
В чем заключается свойство инвариантности формы дифференциала функции?
-
На чем основано применение дифференциала в приближенных вычислениях?
-
Сформулируйте определение производной высших порядков.
-
Каков механический смысл второй производной?
-
Сформулируйте теорему Ролля. Каков ее геометрический смысл?
-
Сформулируйте теорему Лагранжа. Каков ее геометрический смысл?
-
Сформулируйте правило Лопиталя для раскрытия неопределенностей вида
или
.
Приведите примеры. -
Сформулируйте определение возрастающей и убывающей на отрезке функции.
-
Выведите достаточный признак возрастания функции.
-
Сформулируйте определение точки максимума и минимума.
-
Сформулируйте два правила для отыскания экстремумов функции.
-
Приведите пример, доказывающий, что обращение в некоторой точке производной в нуль не является достаточным условием наличия в этой точке экстремума функции.
-
Как найти наименьшее и наибольшее значения функции, дифференцируемой на отрезке? Всегда ли они существуют?
-
Сформулируйте определения выпуклости и выгнутости линии, точки перегиба.
-
Как находятся интервалы выпуклости и вогнутости и точки перегиба линии, заданной уравнением
?
Приведите пример. -
Сформулируйте определение асимптоты линии.
-
Как находятся вертикальные асимптоты линии, заданной уравнением
?
Приведите пример. -
Как находятся невертикальные асимптоты линии, заданной уравнением
?
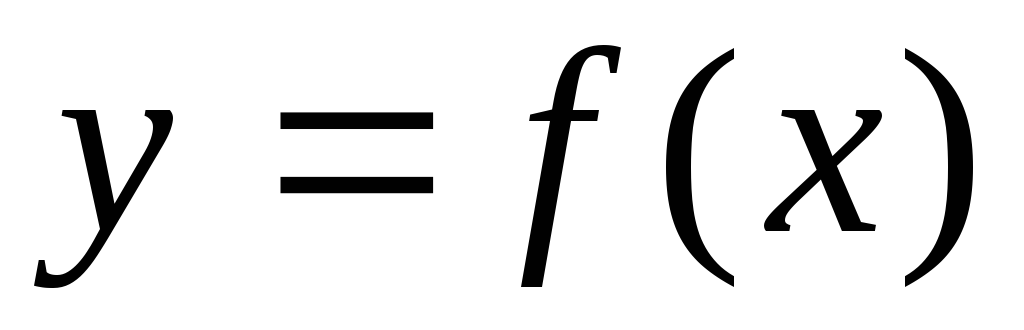Приведите пример. -
Изложите схему общего исследования функции и построения ее графика.
Некоторые типовые примеры с решениями
Раздел 1.
Пример 1.1. Решить систему линейных уравнений, пользуясь формулами Крамера.
Определитель данной системы
Вычислим определитель
,
и
:
.
.
.
Решение системы:
Для того чтобы
убедиться в правильности решения,
подставим эти значения
в исходную систему
Раздел 2.
Пример 2.1.
Найти угол φ между векторами
и
,
если М1(1,
-2, -3), М2(-3,
1, 1), М3(3,
2, 2).
Решение. Для нахождения cosφ используем формулу
,
где
- скалярное произведение векторов
и
.
Определим координаты
векторов
и
cosφ:
= {-3-1,
1+2, 1+3}
={-4,
3, 4},
=
{3-1,
2+2, 2+3}
= {2,
4, 5},
,
φ = 87045'54».
Пример 2.2. Даны координаты вершин пирамиды А1(1, -2, -3), А2(-3, 1, 1), А3(4, 3, -1), А4(3, 2, 2). Найти площадь грани А1 А2 А3 и объем пирамиды.
Решение.
1. Площадь треугольника А1А2А3 найдем, используя геометрический смысл векторного произведения векторов
,
где
-
векторное произведение векторов.
,
.
Вначале находим
,
а затем
ед2.
2.Объем пирамиды найдем, используя геометрический смысл смешанного произведения векторов
,
следовательно,
ед3.