
- •Изменение геметрических характеристик при преобразовании прямоугольных координат
- •Связь моментов относительно параллельных осей
- •Порядок вычислеия геометрических характеристик сложных поперечных сечений
- •Пример определения геометрических характеристик сложного поперечного сечения
- •Исходные данные:
- •Решение
- •Контрольные вопросы по теме «геометрические характеристики поперечного сечения»
- •Решение некоторых типовых задач
- •Решение
- •Решение
- •Геометрические характеристики простейших поперечных сечений
- •Пример численного расчета данного задания на эвм с применением прикладного пакета mathematica 5
Федеральное агентство по образованию
Казанский государственный архитектурно-строительный университет
Кафедра сопротивления материалов и основ теории упругости и пластичности
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ СЛОЖНЫХ СЕЧЕНИЙ СОСТАВНЫХ СТЕРЖНЕЙ
Методические указания для выполнения расчетно-графического задания студентами специальностей 270102, 270109,270112, 270114,270115, 270201,240400,290600,291000
Казань 2009
ОСНОВНЫЕ ПОНЯТИЯ И ФОРМУЛЫ
Р ассмотрим
некоторые основные геометрические
характеристики поперечных сечений.
Пусть дано произвольное поперечное
сечение бруса в системе координат
ассмотрим
некоторые основные геометрические
характеристики поперечных сечений.
Пусть дано произвольное поперечное
сечение бруса в системе координат
![]() .
Выделим элементарную площадку
.
Выделим элементарную площадку
![]() с координатами
с координатами
![]() и
и
![]() .
Введем следующие соотношения и
определения:
.
Введем следующие соотношения и
определения:
-
Площадь плоской фигуры можно представить в виде суммы площадок
 .
Это записывается в виде:
.
Это записывается в виде:
![]() ,
[см2]
,
[см2]
-
Статические моменты относительно осей
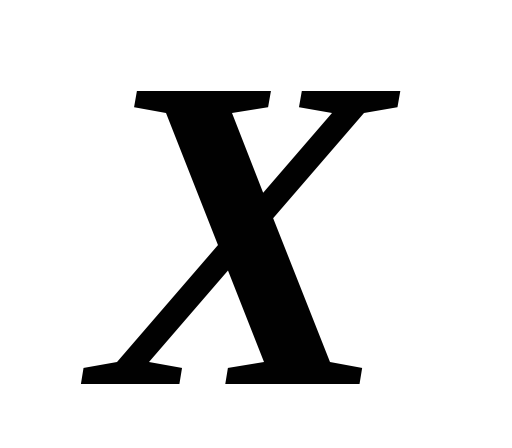 и
и
 определяются как суммы произведений
плеча площадки
определяются как суммы произведений
плеча площадки
 на
на
величину
![]() :
:
![]() ,
,
![]() ,
[см3]
,
[см3]
-
На основании известной из теоретической механики теоремы о моменте равнодействующей статические моменты
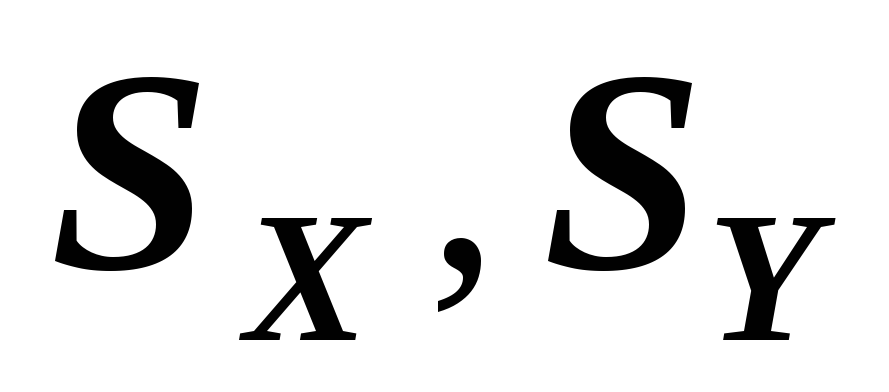 могут быть вычислены по более простым
формулам
могут быть вычислены по более простым
формулам
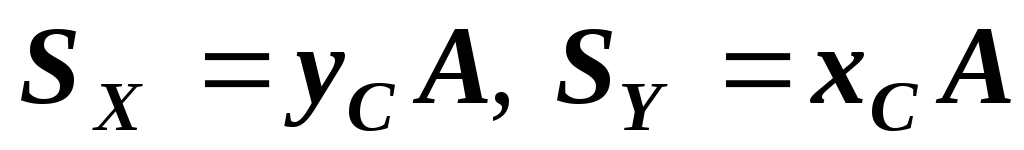 .
Отсюда вытекает, что
центр
тяжести
плоской фигуры
определяется как:
.
Отсюда вытекает, что
центр
тяжести
плоской фигуры
определяется как:
![]() ,
,
![]() ,
[см]
,
[см]
-
Осевыми
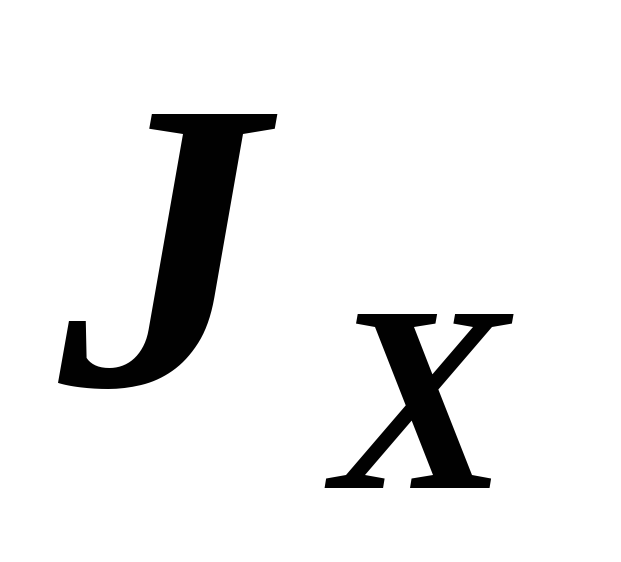 ,
,
 и центробежным
и центробежным
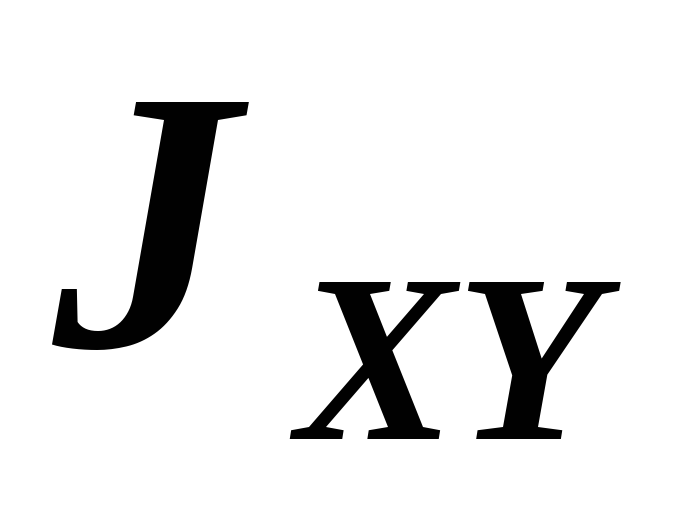 моментами
инерции фигуры
называются геометрические характеристики
численно равные интегралам:
моментами
инерции фигуры
называются геометрические характеристики
численно равные интегралам:
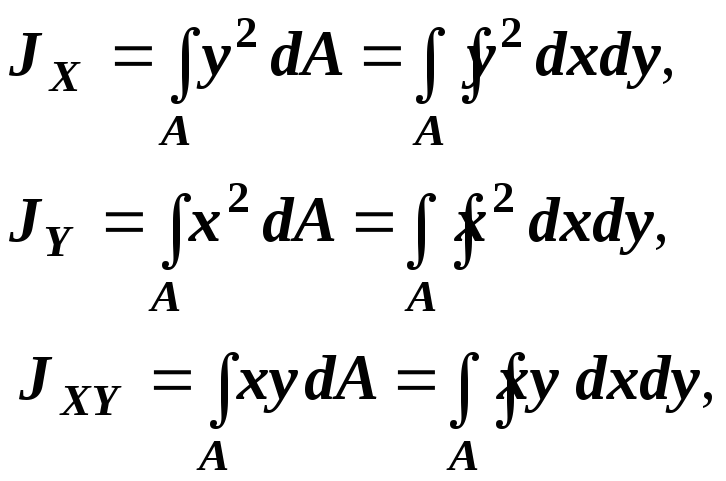 [см4]
[см4]
-
Полярный момент инерции фигуры вводится соотношением:
![]() ,
[см4]
,
[см4]
-
В некоторых расчетах вводятся радиусы инерции плоской фигуры. Относительно осей
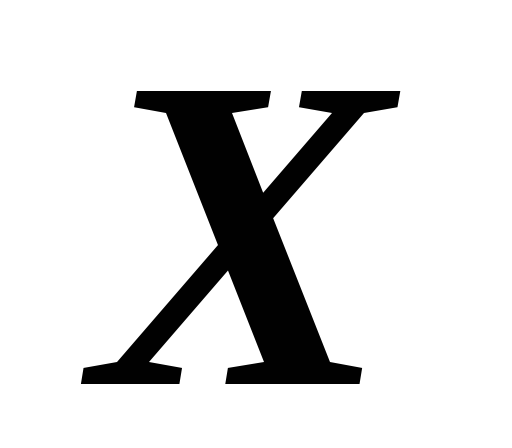 и
и
 они имеют вид:
они имеют вид:
![]() ,
[см]
,
[см]
Замечание: Статические и центробежный моменты в зависимости от выбора системы координат могут быть положительными, отрицательными и равными нулю. Осевые и полярные моменты инерции всегда положительны (это видно из их определений).
Изменение геметрических характеристик при преобразовании прямоугольных координат
-
Связь моментов относительно параллельных осей
(параллельный перенос осей координат)
П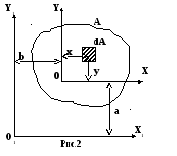 усть
известны все геометрические характеристики
сечения
усть
известны все геометрические характеристики
сечения
![]() относительно осей
относительно осей
![]() и
и
![]() ,
которые параллельны осям
,
которые параллельны осям
![]() и
и
![]() (рис.2).
(рис.2).
Координаты
элементарной площадки
![]() в системе координат
в системе координат
![]() примут вид:
примут вид:
![]() ,
,
Статические моменты
сечения
![]() относительно системы координат
относительно системы координат
![]() имеют вид:
имеют вид:
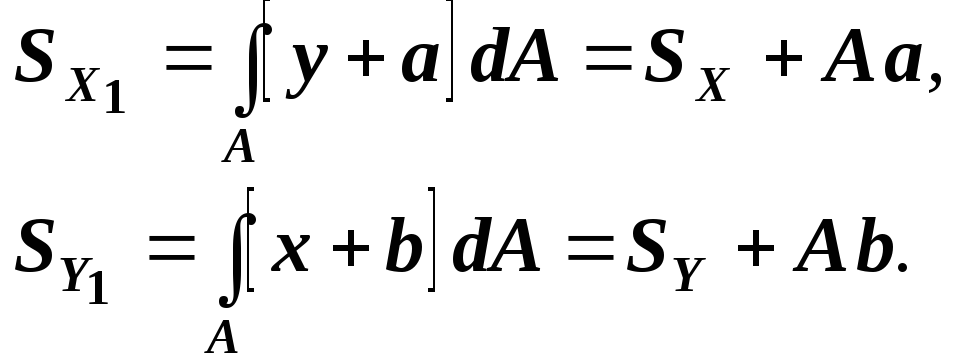 (1)
(1)
Оси, проходящие через центр тяжести сечения, называются центральными осями. Относительно центральной оси статический момент равен нулю.
Таким образом,
если оси
![]() и
и
![]() - центральные, то
- центральные, то
![]() ,
из формулы (1) следует:
,
из формулы (1) следует:
![]()
Моменты инерции
относительно системы координат
![]() определяются как:
определяются как:
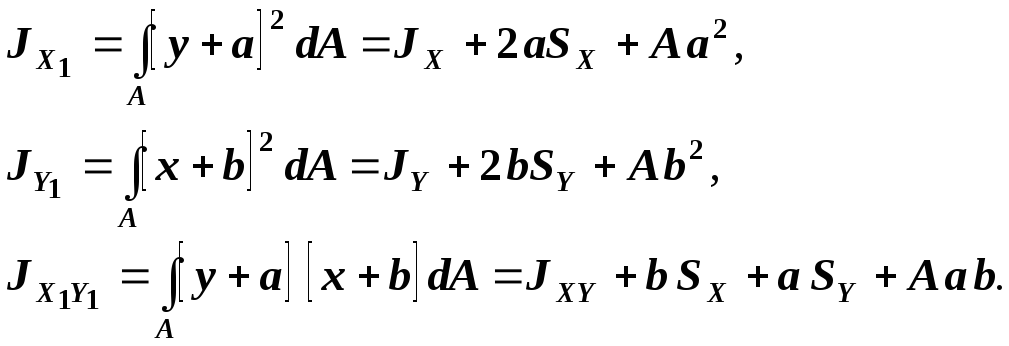 (2)
(2)
Если оси
![]() и
и
![]() - центральные (рис.3), то
- центральные (рис.3), то
![]() ,
и соотношение (2) упрощается:
,
и соотношение (2) упрощается:
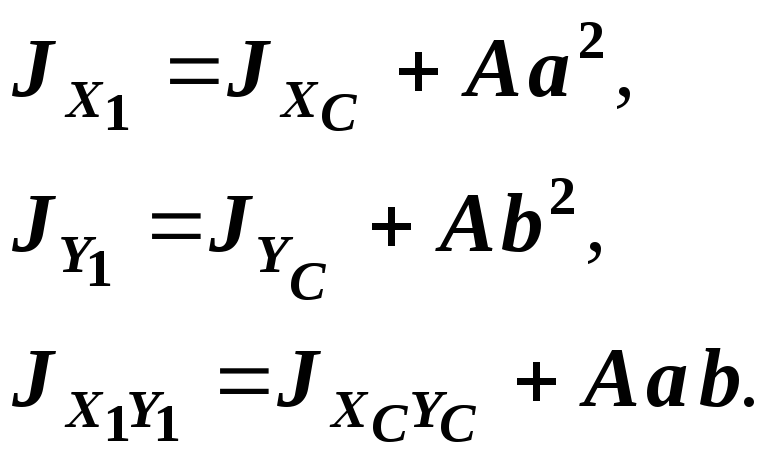 (3)
(3)
Если наоборот,
необходимо найти
![]() то из (3) вытекает:
то из (3) вытекает:
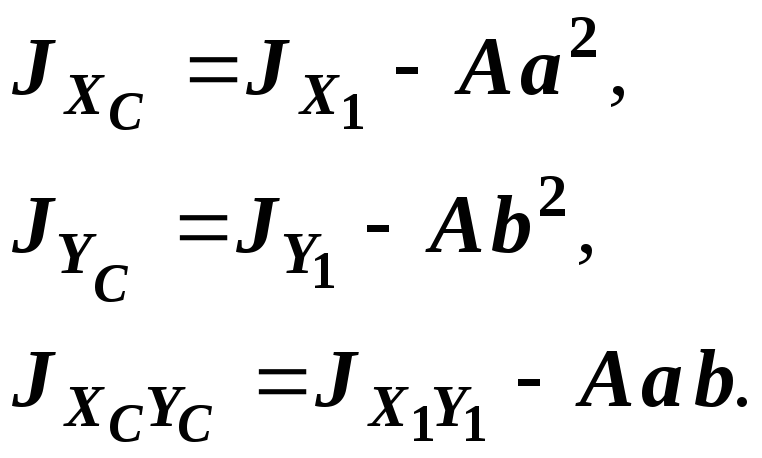 (4)
(4)
б) Поворот осей координат
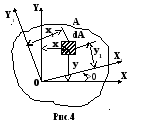 Повернем
оси
Повернем
оси
![]() на угол
на угол
![]() против часовой стрелки, считая угол
поворота осей в этом направлении
положительным. Получим оси
против часовой стрелки, считая угол
поворота осей в этом направлении
положительным. Получим оси
![]() .
.
Координаты
произвольной элементарной площадки
![]() и
и
![]() выразятся через старые координаты
выразятся через старые координаты
![]() и
и
![]() следующим образом:
следующим образом:
![]()
Статические моменты в новых осях примут вид:
![]()
Моменты инерции
относительно осей
![]() и
и
![]() повернутых относительно первоначальных
повернутых относительно первоначальных
![]() ,
,![]() на угол
на угол
![]() примут вид:
примут вид:
 (5)
(5)
Следствие:
Из (5) вытекает, что
сумма
моментов инерции относительно любых
взаимно перпендикулярных осей
![]() и
и
![]() не меняется при их повороте:
не меняется при их повороте:
![]() (6)
(6)
Оси, относительно
которых центробежный момент инерции
обращается в нуль, называются главными
осями инерции.
Относительно этих осей осевые моменты
инерции принимают экстремальные значения
и называются главными
моментами инерции
и обозначаются
![]() и
и
![]() .
.
Действительно,
если, например, взять первую производную
от
![]() , то из условия
, то из условия
![]() вытекает, что
вытекает, что
![]() .
Таким образом это означает, что
.
Таким образом это означает, что
![]() будет принимать экстремальное значение
относительно главной оси
будет принимать экстремальное значение
относительно главной оси
![]() .
Аналогично, момент инерции
.
Аналогично, момент инерции
![]() будет принимать экстремальное значение
относительно главной оси
будет принимать экстремальное значение
относительно главной оси
![]() .
.
Таким образом,
если оси
![]() - главные оси инерции, то главные моменты
инерции можно определить из первых двух
соотношений (5), а последнее соотношение
в (5) для центробежного момента должно
обращаться в нуль (
- главные оси инерции, то главные моменты
инерции можно определить из первых двух
соотношений (5), а последнее соотношение
в (5) для центробежного момента должно
обращаться в нуль (![]() ).
).
Замечание: Главные моменты инерции можно определить и по следующим выражениям:
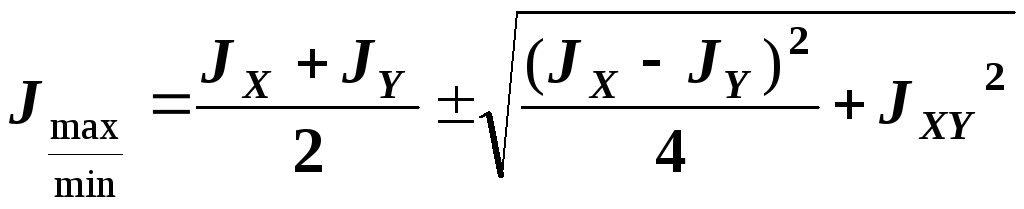 (7)
(7)
Главные оси инерции, проходящие через центр тяжести сечения, называются главными центральными осями.
Таким образом,
согласно третьему соотношению (5) угол
![]() между главной осью
между главной осью
![]() и осью
и осью
![]() определится как:
определится как:
![]() (8)
(8)
Угол
![]() считается положительным, если он отложен
против хода часовой стрелки от оси
считается положительным, если он отложен
против хода часовой стрелки от оси
![]() .
.
Порядок вычислеия геометрических характеристик сложных поперечных сечений
Цель работы:
Найти положение главных центральных осей и вычислить главные моменты инерции составного сечения.
Исходные данные к выполнению расчетно-графического задания выбираются из сборника заданий к расчетно-графическим работам по курсу «Сопротивление материалов с основами теории упругости и пластичности» согласно шифру, выданного каждому студенту преподавателем. Это пособие также определяет объем и последовательность выполнения работы.
При расчетах используются таблицы сортамента (части стандартных профилей прямоугольниками не заменять).
Порядок выполнения работы: Построим данное сечение в выбранном масштабе, согласно всем необходимым для данного задания геометрическим параметрам.
1)
Выберем первоначальные оси координат
![]() .
Для того, чтобы упростить путь вычисления
статических моментов и моментов инерции
целесообразно направить оси так, чтобы
все сечение находилось в первой четверти
относительно осей
.
Для того, чтобы упростить путь вычисления
статических моментов и моментов инерции
целесообразно направить оси так, чтобы
все сечение находилось в первой четверти
относительно осей
![]() .
.
2) Данное поперечное сечение состоит из простейших геометрических фигур: прямоугольника, двутавра (швеллера) и равнобокого уголка.
В каждой простой
фигуре проведем собственные центральные
оси
![]() ,
параллельные осям
,
параллельные осям
![]() .
В первоначальных осях
.
В первоначальных осях
![]() определим координаты центров тяжести
каждой простой фигуры
определим координаты центров тяжести
каждой простой фигуры
![]() .
.
3)
Найдем положение центра тяжести всего
сечения в первоначальных осях
![]() ,
т.е. координаты
,
т.е. координаты
![]() :
:
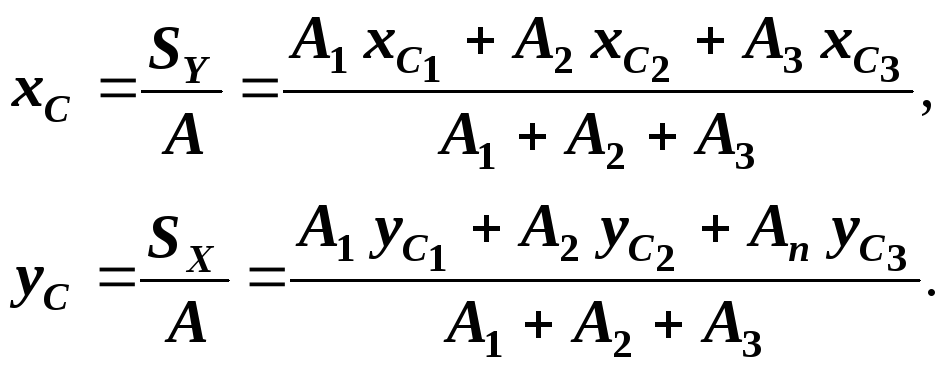 (9)
(9)
где
![]() -
площадь
-
площадь
![]() -
ой фигуры.
-
ой фигуры.
Проведем через
центр тяжести (точку
![]() )
оси
)
оси
![]() и
и
![]() параллельно первоначальным осям
параллельно первоначальным осям
![]() .
Это будут центральные оси всего сечения.
.
Это будут центральные оси всего сечения.
-
Вычислим моменты инерции каждой простой фигуры относительно первоначальных осей
 по формулам параллельного переноса
(3):
по формулам параллельного переноса
(3):
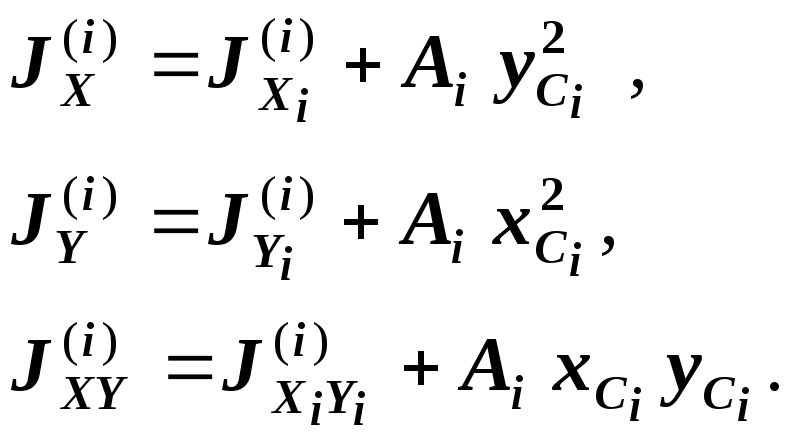
![]() (10)
(10)
где
![]() ,
,![]() - осевые и центробежный моменты инерции
- осевые и центробежный моменты инерции
![]() -
ой фигуры относительно первоначальных
осей.
-
ой фигуры относительно первоначальных
осей.
![]() ,
,![]() -
осевые и центробежный моменты инерции
-
осевые и центробежный моменты инерции
![]() -
ой фигуры относительно собственных
центральных осей.
-
ой фигуры относительно собственных
центральных осей.
Для всего сложного
сечения моменты инерции относительно
осей
![]() определятся суммированием:
определятся суммированием:
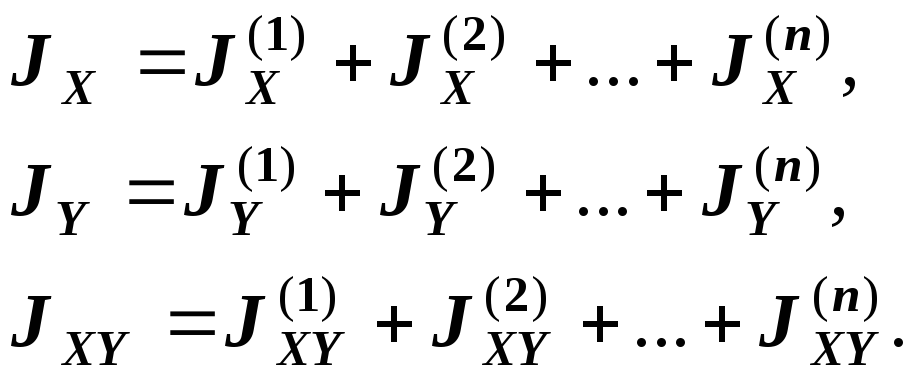 (11)
(11)
5)
Вычислим моменты инерции всего сечения
относительно центральных осей
![]() и
и
![]() согласно формуле (4):
согласно формуле (4):
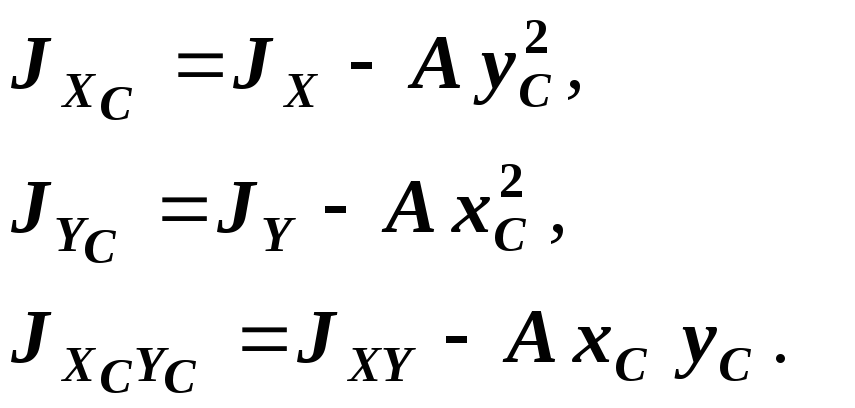 (12)
(12)
Если
![]() ,
то оси
,
то оси
![]() будут только центральными осями, но не
главными.
будут только центральными осями, но не
главными.
6)
Определим положение главных центральных
осей сечения. Согласно соотношению (8)
главная центральная ось сечения
![]() расположена под углом
расположена под углом
![]() к центральной оси
к центральной оси
![]() :
:
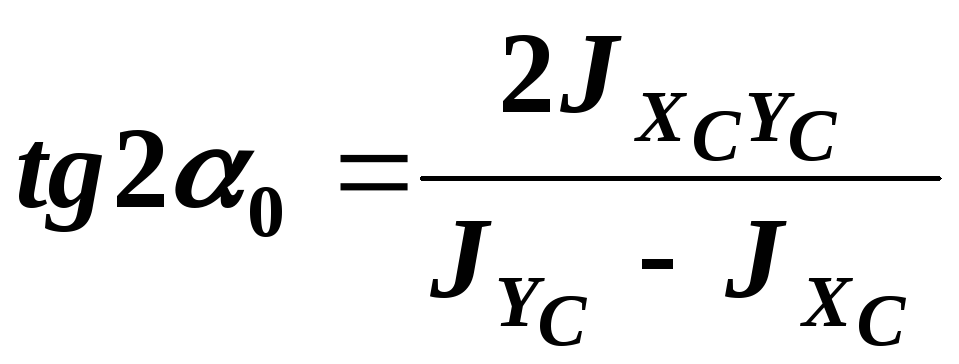 (13)
(13)
Положительные
значения
![]() откладывают от оси
откладывают от оси
![]() против хода часовой стрелки, отрицательные
- по ходу часовой стрелки.
против хода часовой стрелки, отрицательные
- по ходу часовой стрелки.
7)
Вычислим главные моменты инерции сечения
![]() .
.
Моменты инерции можно определить по формулам (5):
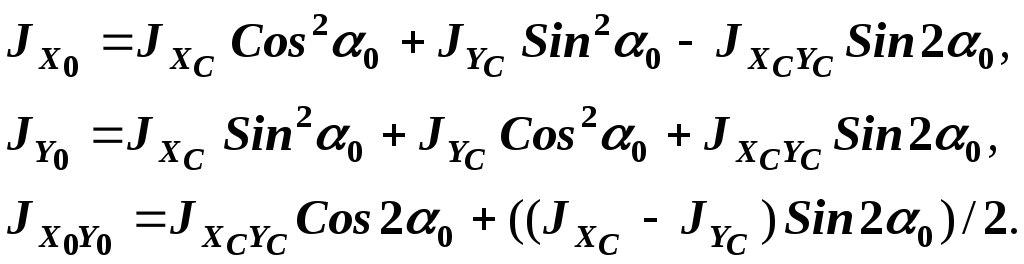 (14)
(14)
Замечание:
Последнее
соотношение в (14) проверочное, так как
относительно главных центральных осей
центробежный момент инерции должен
быть равен нулю, т.е.
![]() .
.
Главные моменты инерции можно определить и по соотношению (7).
8)
Вычислим моменты инерции относительно
центральных осей
![]() ,
расположенных под углом
,
расположенных под углом
![]() к главным центральным осям
к главным центральным осям
![]() .
Для этого необходимо воспользоваться
соотношениями (5) с учетом того, что
.
Для этого необходимо воспользоваться
соотношениями (5) с учетом того, что
![]() :
:
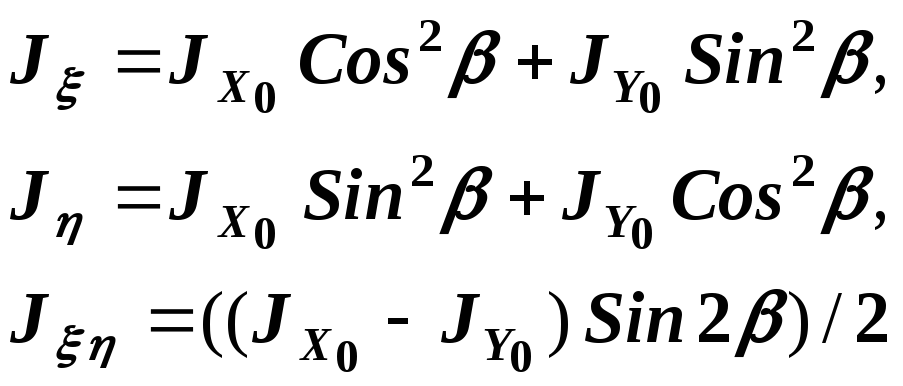 (15)
(15)
9) Произведем проверку вычислений. Для этого нужно воспользоваться соотношением (6):
![]() (16)
(16)
