Функции делятся на 2 класса

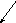
Элементарные неэлементарные

(специальные)

Элементарные функции изучаются в школьной математике и делятся на:

1. Базисные

а) Степенные y = xⁿ

б) Показательные y = a^x

в) Тригонометрические y = sin x

2. Остальные:

f

X Y

f ^-1 (обратная функция)

Обратные показательным – логарифмические функции.

Обратные тригонометрическим – arc…

Пример:

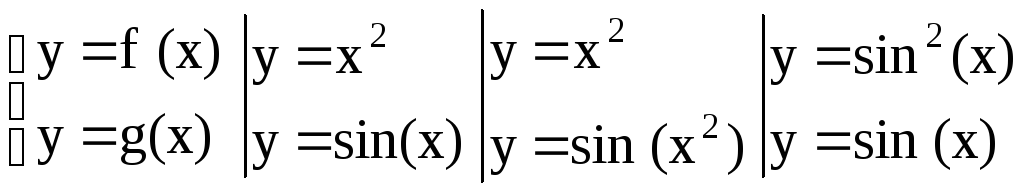
y = f (g(x)) – сложная функция – композиция элементарных функций.

Элементарными функциями называются функции, полученные из элементарных базисных функций с помощью алгебраических операций и операций композиции.

Г(f) – график функции.

График функции есть множество точек (x, y), где y = f(x).

Общие свойства функций:

1. Четность –

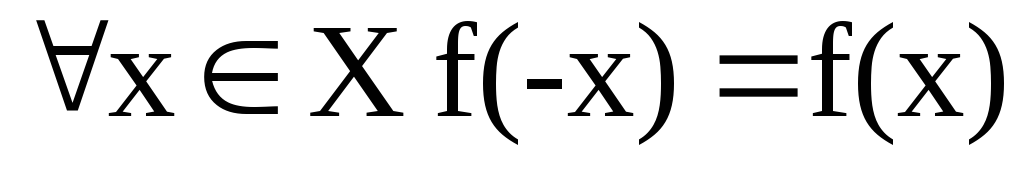
2. Нечетность –

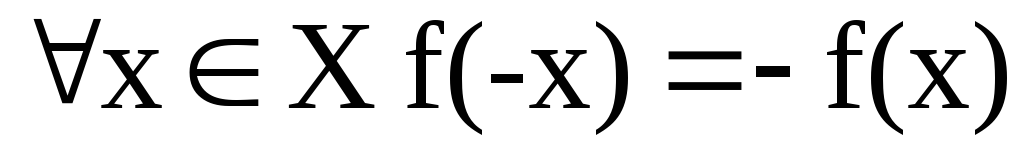
3. Периодичность –

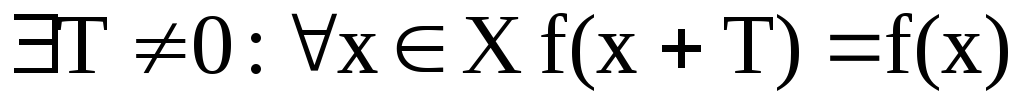
Рисунок

f(x) – ограниченная сверху, если

f(x) – ограниченная снизу, если

f(x) – ограниченная, если

f(x) – монотонная, если она постоянно возрастает или постоянно убывает

Если y = f(x), то Д – область определения данной функции.

Свойства модулей суммы и разности:

Теория пределов

Число b называется пределом функции в точке а, если для любой – окрестности точки b существует – окрестность точки а.

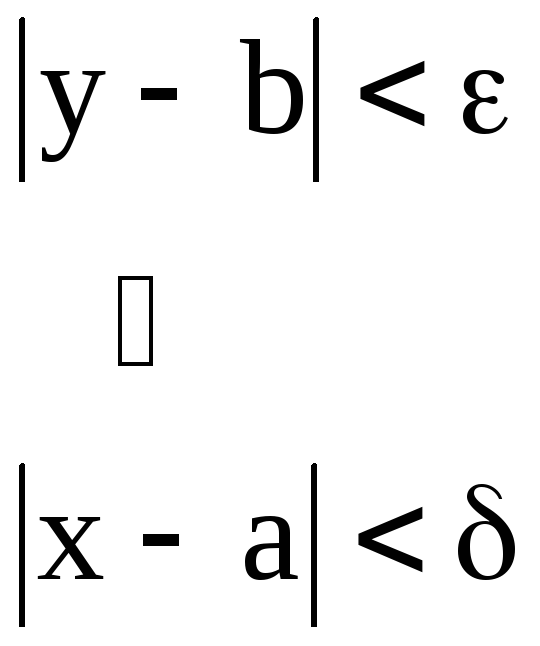
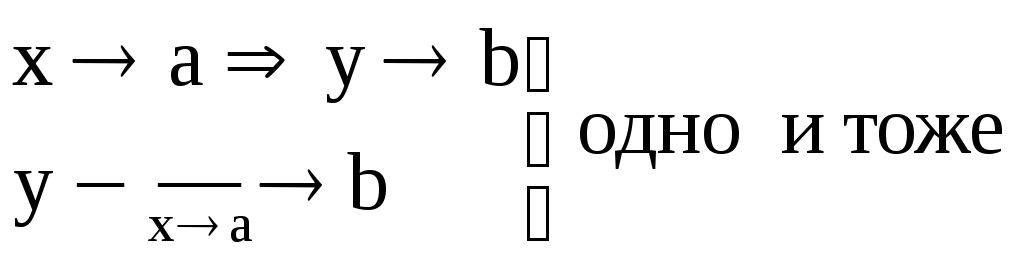
– предел функции при , равный b.

Число b называется пределом функции при неограниченном возрастании аргумента . Для любого существует такое N, и если , то .

П римеры:

y = f(x) =

y = f(x) = x²

1. 

2. 

Пример:

y =, когда ,

Неопределенности.

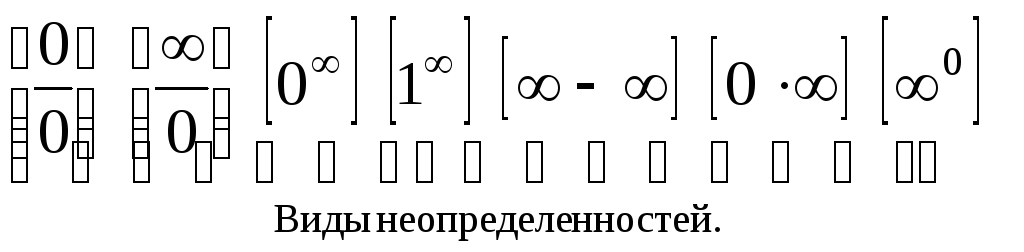
Раскрытие неопределенностей.

Теорема об ограниченности функции, имеющей предел.

Если функция f(x) имеет предел в точке a ,то она ограниченна в некоторой окрестности точки a.

Доказательство:

Пусть , тогда , отсюда получаем . Обратное неверно.

Контрольный пример:

в окрестности точки 0.

– не существует.

Рис (необязательно).

Бесконечно малой величиной при называется функция, предел которой в точке a равен 0.

– бесконечно малая величина (б.м.в.).

1. – бесконечно малая величина при

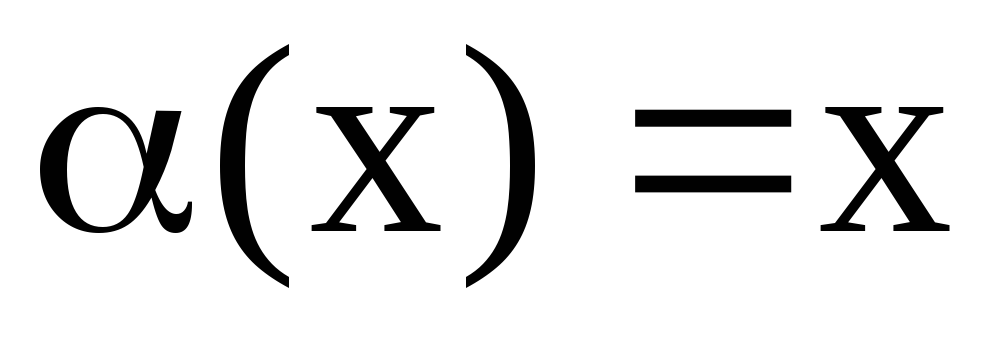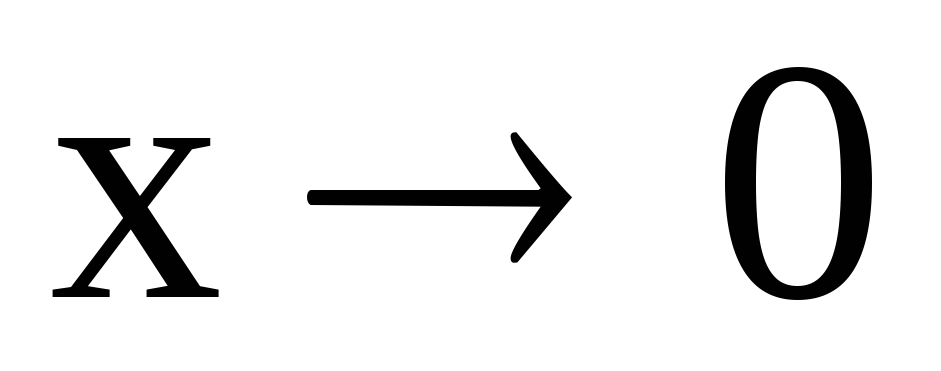
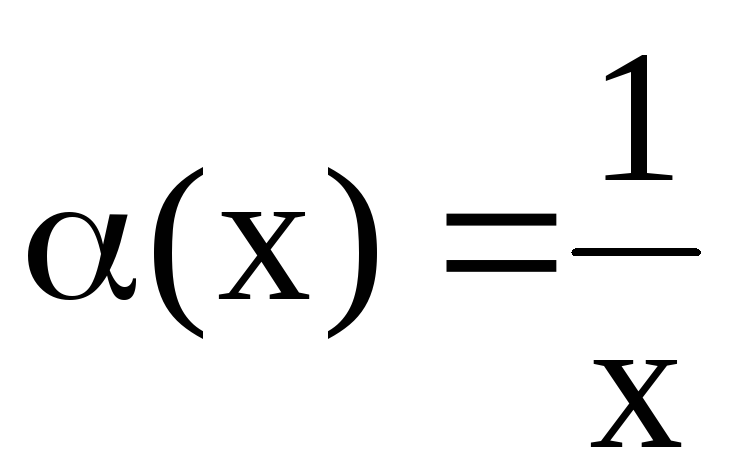2. – бесконечно малая величина при

Бесконечно большой величиной при называется функция неограниченно возрастающая.

– бесконечно большая величина (б.б.в.)

Любая бесконечно большая величина неограниченна.

Теорема о связи предела и бесконечно малой величины.

Если , то , где – бесконечно малая величина. Или .

Доказательство:

Допустим, что , тогда .

, значит , –

бесконечно малая величина.

Пример:

f(x) = x² + 1

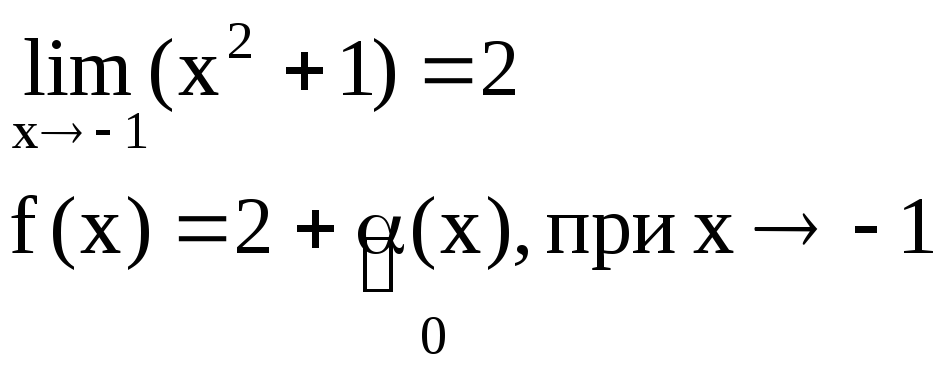
Теорема о связи бесконечно малой и бесконечно большой величиной.

Если – бесконечно малая величина при – бесконечно большая величина.

Если – бесконечно большая величина при – бесконечно малая величина.

Доказательство:

Допустим, что – бесконечно малая величина при , то , что . Значит

Следствие: и

Свойства бесконечно малых величин:

1) Алгебраическая сумма бесконечно малых величин есть бесконечно малая:

Доказательство:

или , значит – бесконечно малая величина.

2) Произведение бесконечно малой величины на ограниченную функцию есть бесконечно малая: , где f(x) – ограниченная.

Доказательство:

, значит – бесконечно малая величина.

3) Частное от деления бесконечно малой величины на любую функцию, предел которой не равен 0, есть бесконечно малая: при и .

Теоремы о пределах.

Теорема 1. Предел суммы равен сумме пределов, если они существуют:

Доказательство:

Из теоремы о связи между пределом и бесконечно малой величиной следует:

Получаем

Теорема 2. Предел произведения равен произведению пределов, если они существуют:

Доказательство:

Из теоремы о связи между пределом и бесконечно малой величиной следует:

Получаем

Теорема 3. Предел частного равен частному пределов: 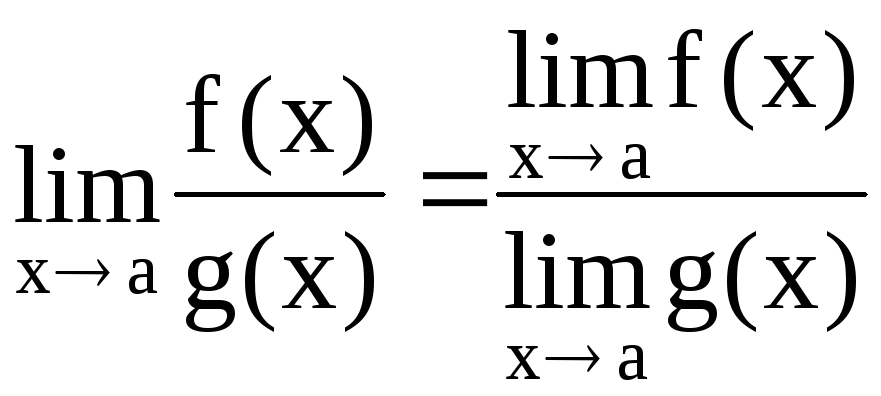. При условии: все пределы существуют и .

Доказательство:

Из теоремы о связи между пределом и бесконечно малой величиной следует:

Получаем

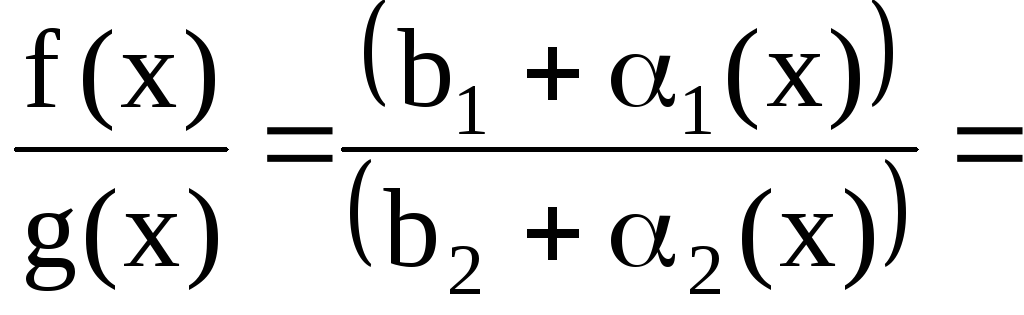
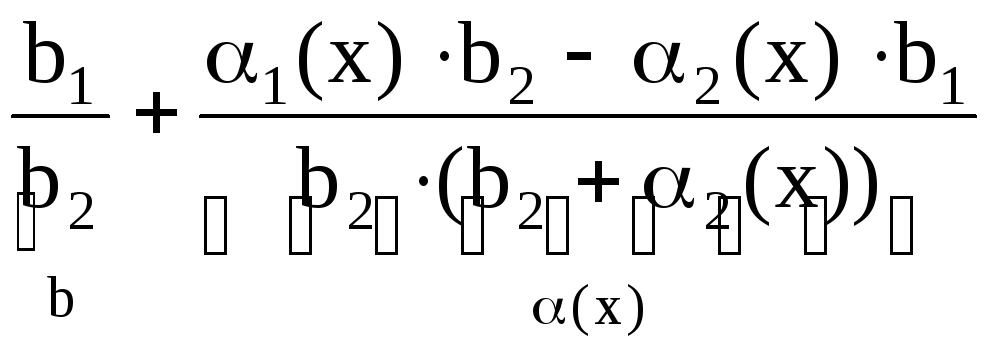
Теорема 4. Предел сохраняет знак неравенства.

Если .

Доказательство:

Следовательно,

Следствие:

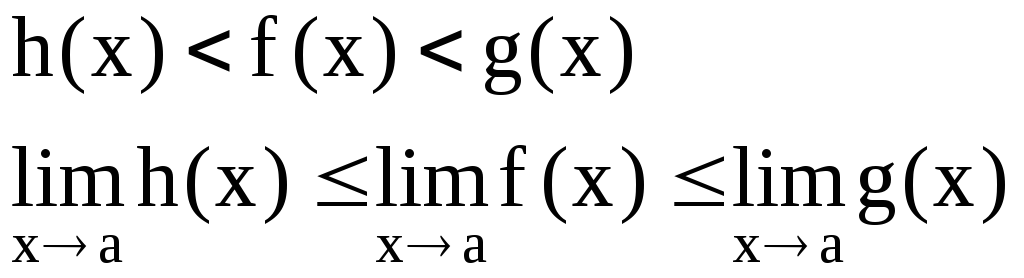
Теорема 5. Если функция ограниченна и монотонна на (a, b), то она имеет предел:

Теорема 6. Критерий Коши.

Если ,

тогда и только тогда .

Приемы раскрытия неопределенностей.

1) Выделение общего множителя (для неопределенности ).

Пример:

2) Умножение на сопряженное выражение (для неопределенности ).

Пример:

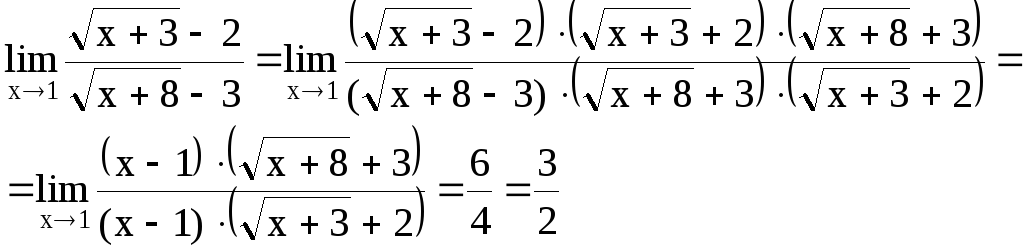
3) Выделение главной части (для неопределенности ).

Примеры:

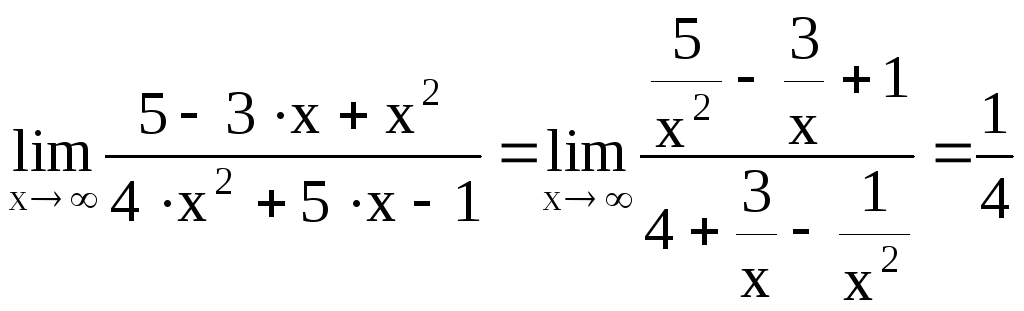
Теорема. Первый замечательный предел .

Доказательство (геометрическое):

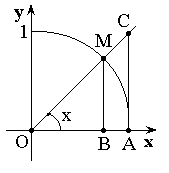
Так как , то .

Следствия из теоремы:

1)

2)

3)

4)

5)

Теорема. Второй замечательный предел .

Доказательство:

Бином Ньютона.

, где .