Федеральное агентство по образованию

Федеральное государственное образовательное учреждение

высшего профессионального образования

Казанский государственный архитектурно-строительный университет

Кафедра Сопротивления

материалов и основ теории

упругости

Построение эпюр внутренних силовых факторов при плоском изгибе балки

Методические указания

для выполнения расчетно-графического задания

студентами специальности: 1203, 1205, 1207,

1208, 1210, 1211

Казань

2007

Излагается основной порядок построения эпюр внутренних силовых факторов при плоском изгибе различных балок, статически определимых рам, плоских криволинейных брусьев, очерченных по радиусу, при различных условиях их закрепления и нагружения. Даны числовые примеры построения эпюр.

Составитель: Мартышев В.П., к.т.н., доцент кафедры

сопротивления материалов и основ теории

упругости, КГАСУ

Рецензент: Паймушин В.Н., д.ф-м.н., профессор

Зав. Кафедрой сопротивления материалов,

КАИ

Исходные данные к выполнению расчетно-графического задания выбираются из "Заданий и методических указаний к расчетно-графическим работам по курсу сопротивления материалов" согласно шифру, выданному каждому студенту.

Вводная часть

Будем рассматривать изгиб в вертикальной плоскости , т.е. изгиб относительно оси .

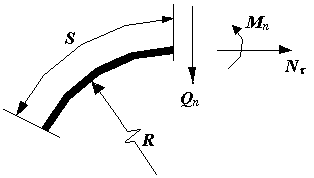
В поперечных сечениях бруса в этом случае могут возникнуть следующие внутренние усилия: продольная сила, перерезывающая сила, изгибающий момент. Как и в общем случае деформирования бруса в пространстве внутренние силовые факторы при плоском изгибе определяются методом сечений [1]. На торце левой отсеченной части , если их направления совпадают с положительными направлениями осей и , , если его вращательный эффект с положительного конца оси виден направленным против хода часовой стрелки. На торце правой части внутренние силовые факторы равны по величине и противоположно направлены внутренним усилиям на торце левой отсеченной части.

х

у

z

+Q_y

+Q_y

+M_x

+M_x

+N_z

+N_z

Внутренние силовые факторы, действующие на торце левой отсеченной части, определяются через внешние силы, действующие на левую отсеченную часть по известным зависимостям [1], следующим из условий равновесия левой отсеченной части:

(1)

На торце правой отсеченной части внутренние усилия определяются через внешние нагрузки, действующие на эту часть:

(2)

В формулах (1) и (2) составляющие внешних нагрузок и моменты от них относительно оси (которую при этом располагают в исследуемом сечении бруса) следует суммировать с учетом знаков. Для этого как и в [1] условимся о знаках:

1. положительные направления составляющих внешней нагрузки и совпадают с направлениями осей и ;

2. моменты от внешней нагрузки относительно оси (расположенной в данном сечении бруса) положительны, если их вращательные эффекты направлены против хода часовой стрелки (ось всегда направляем «на нас»). Эти правила справедливы как для левой отсеченной части бруса, так и для правой.

Если вычислить внутренние силовые факторы в ряде сечений по длине бруса и графически изобразить закон их изменения по длине бруса, получим эпюры и .

При определении внутренних усилий в брусе наряду с внешними нагрузками необходимо учитывать в большинстве задач и опорные реакции.

Неподвижность балки в вертикальной плоскости обеспечивают три опорные реакции. Для их определения можно составить три уравнения равновесия балки. Эти уравнения желательно составлять так, чтобы в каждое из них входила только одна неизвестная опорная реакция. Обычно составляют два уравнения моментов относительно оси , проходящей через опоры и сумму проекций на ось всех сил, действующих на балку. Из этих уравнений определяют три опорные реакции. Далее обязательно надо сделать проверку опорных реакций. Например, составляют сумму проекций всех сил и опорных реакций на ось , т.е. . В некоторых задачах, например, для бруса с ломаной или криволинейной осью, можно составить другие, более удобные для данной задачи уравнения равновесия бруса, чтобы и в них входило только по одной неизвестной опорной реакции.

Внутренние силовые факторы и в брусе с прямолинейной осью при изгибе в плоскости связаны следующими дифференциальными зависимостями [1]:

(3)

Здесь распределенная (погонная) нагрузка вдоль оси , распределенная (погонная) нагрузка вдоль оси .

Для бруса с криволинейной осью, очерченной по радиусу , внутренние силовые факторы будем обозначать . Они связаны следующими дифференциальными соотношениями [1]:

(4) где криволинейная координата, отсчитываемая вдоль оси бруса. Ниже будет показано, что диф-ференциальные зависимости (3) и (4) можно использовать для более точного

построения эпюр внутренних силовых факторов и проверки этих эпюр.

Основной порядок построения эпюр внутренних силовых факторов

1. Из уравнений равновесия бруса в целом определяются все необходимые опорные реакции. Обязательно делается проверка величин опорных реакций.

2. В соответствии с характером конструкции бруса и его нагружения брус делится на участки (в пределах каждого участка конструкция и нагрузка не должны резко изменяться). Эпюры внутренних силовых факторов строятся по участкам.

3. Мысленно разрезается брус на участке и рассматривается та его часть, где меньше внешних нагрузок. Сечение разреза определяется текущей координатой (задавая границы ее изменения в пределах участка). Рассматривая выбранную отсеченную часть бруса и пользуясь формулами (1) и (2), записывают аналитические выражения для внутренних и 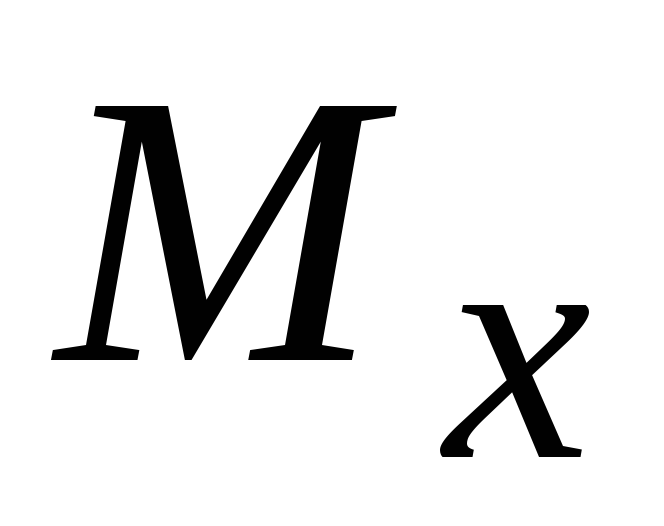в функции от текущей координаты участка.

4. Задаваясь несколькими значениями текущей координаты в пределах участка, вычисляют по полученным формулам величины и знаки и в этих сечениях бруса. Положительные значения внутренних и откладываем в масштабе вниз от оси бруса (по оси ), отрицательные вверх.

5. Согласно дифференциальным зависимостям (3) и (4) выясняем наличие в пределах участка особых сечений, где внутренние силовые факторы принимают экстремальные значения, находим их величины. Соединяя все полученные точки для каждого силового фактора в пределах участка линией, соответствующей характеру аналитической зависимости, строим отдельно эпюры и .

6. Для брусьев с прямолинейной осью делается проверка построения эпюр внутренних силовых факторов:

Рис.1

а) Обозначим , где угол наклона к оси касательной к эпюре , т.к. , то тангенс угла наклона касательной к эпюре в любом сечении бруса должен быть равен в этом же сечении. отсчитывается от оси по ходу часовой стрелки. Эпюры и проверяются при движении вдоль оси .

б) Обозначим , где угол наклона к оси касательной к эпюре , т.к. , то тангенс угла наклона касательной к эпюре в любом сечении бруса должен быть равен в этом сечении (вниз). отсчитывается от оси по ходу часовой стрелки. Соответствие эпюры приложенной погонной нагрузке бруса проверяется также при движении вдоль оси .

в) Скачки в эпюре численно должны быть равны локальным поперечным силам , приложенным в этих сечениях бруса, а скачки в эпюре локальным изгибающим моментам .

Примечание: Наличие скачка в эпюре без присутствия соответствующего локального силового фактора и наоборот, свидетельствуют об ошибочности эпюры.

Примеры построения эпюр внутренних силовых факторов для различных брусьев

Пример №1 (рис. 1).

Дано: кН/м,

м