Лекия-22 коллекторный модулятор

При коллекторном модуляторе используется зависимость I_к = Ф(Е_к), при этом U_ω – подается в цепь базы, а U_Ω – в цепь коллектора. Е₀ – для выбора начальной рабочей точки.

У ламп большое внутреннее сопротивление и следовательно высокоомная R_ое.

Основной характеристикой коллекторного модулятора является мо­дуляционная характеристика, которая определяет его качество и режим ра­боты.

1. Выделяем линейный участок на СMX.

2. Выбираем рабочую точку Е_к.

3. Определяем U_Ωmax ≥ U_Ω

Лекця-22 методы получения однополосных сигналов

1. Амплитуда несущей не нужна, существуют две боковые полосы с AM без несущей.

2. Без несущей, одна боковая полоса с AM.

3. Одна БП с AM с остатками несущей.

4. 0БП - AM с пилосигналом.

Существует два метода получения сигнала с одной боковой полосой (ОБП):

1. Метод фильтрации.

2. Метод фазирования.

Рассмотрим метод фильтрации:

Недостатком этого метода является то, что теряется половина мощ­ности (часть энергии).

Рассмотрим метод фазирования:

Лекция-23

СИГНАЛЫ С ЧАСТОТНОЙ И ФАЗОВОЙ МОДУЛЯЦИЕЙ

Так как частота и фаза колебаний (гармонических) связаны между собой через производную и интеграл, т.е. при изменении частоты изменя­ется фаза или при изменении фазы изменяется частота, то ЧМ и ФМ сиг­нал являются сигналами с угловой модуляцией.

(3) аналитическое выражение для ЧМ сигнала

- девиация частоты, т.е. максимальное отклонение частоты в одну сторону.

ФМ для передачи аналоговых (непрерывных сообщений) не исполь­зуется, т.к. при этом не эффективно используется выделенный диапазон частот.

СПОСОБЫ ПОЛУЧЕНИЯ СИГНАЛА С ЧМ

Получения ЧМ сигнала с помощью варикапа

Часто в качестве управляемых реактивных элементов используют реактивный транзистор. Чтобы определить режим и качество работы реак­тивного транзистора, пользуются модуляционной характеристикой БМ.

Для получения ЧМ колебания нужно изменить частоту по закону модулирующего колебания. При подключении варикапа параллельно колебательному контуру будет меняться емкость колебательного контура. Емкость С_з служит для протекания переменной составляющей и для непротекания постоянной составляющей. Емкостное сопротивление варикапа будет малой для переменной составляющей.

Способы получения фм сигнала

Получения ФМ сигнала при помощи управляемого реактивного элемента

Получения ФМ сигнала из AM сигнала

Лекция-24 ПРЕОБРАЗОВАТЕЛЬ ЧАСТОТЫ

Преобразование частоты - перенос спектра входного сигнала из од­ного диапазона частот в другой, не изменяя соотношений между его спек­тральными составляющими. Преобразование частоты возможно в НЭЦ и ПЭЦ.

ЛЕКЦИЯ – 25 ДЕТЕКТИРОВАНИЕ

Детектирование - это процесс, обратный модуляции, в результате которого из ВЧ модулированного колебания выделяется закон изменения информационного параметра.

S

Д

НЭ

ПЭ

ФНЧ

_АМ(t) u(t) S_мод(t) u(t)

Основной характеристикой детекторов является их детекторная ха­рактеристика. Для АД (амплитудный детектор):

U_Ω = I₀ R_n

U_ω

Рассмотрим детектирование AM сигнала:

U(t)

i

S_АМ(t)

C_н R_н

U(t)

Основное условие выбора нагрузки:

В зависимости от уровня входного модулированного сигнала разли­чают два режима работы амплитудных детекторов.

D

i

S_АМ(t) C_н R_н U(t)=U_вых

При слабых сигналах (меньше 0,1 - 0,2В) используется начальный участок ВАХ диода. Так же рассмотрим режим работы амплитудного детектора при сильном сигнале U _вх 0,2В R_n » R_np

i

U_вых

0 u U

Лекция-26 СИНХРОННОЕ ДЕТЕКТИРОВАНИЕ

При синхронном детекторе используется параметрический элемент.

U_гcos(t+)

S_АМ (t),U С_н R_н U_вых

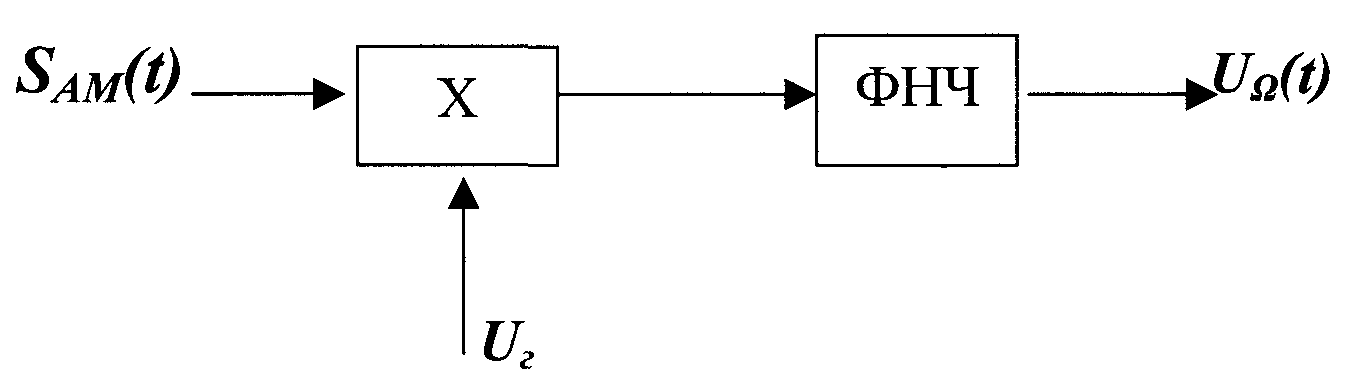
При помощи СД можно детектировать сигналы с одной и той же частотой несущей и различной начальной фазой.

Лекция-27 ДЕТЕКТИРОВАНИЕ СИГНАЛА С ОДНОЙ БОКОВОЙ

ПОЛОСОЙ (ОБП) И ДВУМЯ БП (ДБП) ПРИ ПОМОЩИ СД

СД обладает свойством частотной избирательностью, т.е. способно­стью выделить полезный сигнал из суммы полезного сигнала и мешающе­го.

Лекция-28

ДЕТЕКТИРОВАНИЕ СИГНАЛА С ФАЗОВОЙ МОДУЛЯЦИЕЙ

Лекция-29 ДЕТЕКТИРОВАНИЕ ЧМ СИГНАЛА

ПВМ – преобразователь

АД – амплитудный детектор

ПД – пиковый детектор

ЧАСТОТНЫЙ ДЕТЕКТОР С ОДИНОЧНЫМ РАССТРОЕННЫМ КОНТУРОМ

Работает по принципу преобразователя ЧМ сигнала в AM, с даль­нейшим детектированием при помощи АД.

Если будет изменяться расстройка колебательного контура, это приведет к изменению колебательного контура эквивалентного входного сопротивления колебательного контура, следовательно будет изменен U_к(ω)=I∙Z_к(ω)

ЧАСТОТНЫЙ ДЕТЕКТОР С ДВУМЯ ВЗАИМНО РАССТРОЕННЫМИ КОНТУРАМИ

Недостатки:

1. Наличие катушек индуктивности.

2. Все три катушки настраиваются на разные частоты.

ЧАСТОТНЫЙ ДЕТЕКТОР С ДВУМЯ ВЗАИМНО НАСТРОЕННЫМИ КОНТУРАМИ

Работает по принципу преобразователя ЧМ сигнала в ФМ сигнал.

Лекция-30 КВАДРАТУРНЫЙ ЧД

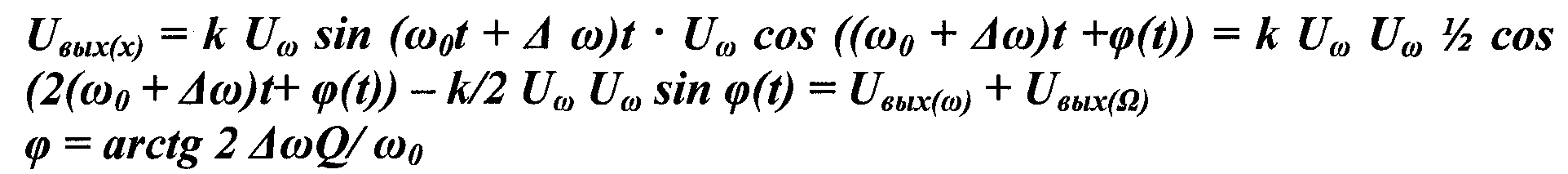
ЧД КАК СЧЕТЧИК ИМПУЛЬСОВ.

Работает по принципу преобразователя ЧМ сигнала в последова­тельность импульсов с постоянной амплитудой и шириной, и с частотой повторений равной частоте входного модулированного сигнала.

ГАРМОНИЧЕСКИЙ ЧД (ГЧД).

ЧМ преобразуется в ФМ сигнал, дальнейшее детектирование при помощи пикового детектора, при этом полезно используется токи первой и второй гармоника входного сигнала.

Лекция-31 СИГНАЛ И ПОМЕХА КАК СЛУЧАЙНЫЙ ПРОЦЕСС

1. Сигнал делится на: непрерывный, и дискретный.

2. Сигналы: сложные и простые.

3. Сигналы: детерминированные и случайные.

Наибольшими общими характеристиками случайных процессов явля­ются интегральный, дифференциальный законы распределения. Законы распределения делятся на одномерные и двумерные.

Одномерный интегральный закон распределения

плотность вероятности

Наиболее полными характеристиками случайных процессов являют­ся его п - мерный интегральный и дифференциальный закон распределе­ний. Наиболее часто для оценки случайных процессов пользуются:

1. Математическим ожиданием, усредненным по времени и по множест­вам (ансамблем) М(х).

2. Функция корреляции делится на: 1. Функцию автокорреляции. 2. Функцию взаимной корреляции. Функция автокорреляции.

Функция взаимной корреляции.

Все случайные процессы делятся на стационарные и нестационар­ные.

Под стационарным процессом в широком смысле понимают такой процесс, n мерный закон распределения которого на зависит от начала от­счета времени.

Стационарный случайный процесс в узком смысле - это такой про­цесс, математическое ожидание и дисперсия которого не зависит от начала отсчета времени. А функция корреляции В_хх (τ) также не зависит от от­дельных значений t₁ и t₂, а зависит от разности t₂ – t₁= τ.

Не стационарный процесс - такой процесс, в котором функция кор­реляции, дисперсия, математическое ожидание зависят от начала отсчета времени.

Коэффициент автокорреляции:

Коэффициент взаимной корреляции:

Стационарные случайные процессы обладают свойством эргодичности.

Лекция-32 СВОЙСТВА ФУНКЦИИ КОРРЕЛЯЦИИ

1. Функция корреляции - четная функция. В(τ) =В(-τ)

2. В_хх (τ) =σ², где σ²- дисперсия случайного процесса.

3. В_хх(τ)≥В_хх(τ)

4. Если R_xx (τ) = 1 при τ = 0, тогда

R_xx (τ) = 0 при τ ≠ 0, то такой процесс называется чисто случайным процессом.

5. Если стационарный случайный процесс не содержит регулярной со­ставляющей, то его функция корреляции В_хх (τ) →а².

6. Если стационарный случайный процесс содержит регулярную состав­ляющую В_хх (τ) →а², где а² - квадрат амплитуды регулярно составляющей.

7. Функция автокорреляции периодического процесса также является пе­риодической с тем же периодом, что и сам процесс. В_ху периодический процесс не зависит от его начальной фазы.

ИНТЕРВАЛ КОРРЕЛЯЦИИ

Для стационарных случайных процессов можно указать такой про­межуток времени Δτ, что как только Δτ > τ, то его отдельные значения ста­новятся независимыми.

Этот промежуток времени Δτ, в пределах которого существует взаи­мосвязь между отельными значениями случайного процесса, называется интервалом корреляции.

Δτ - определяется шириной основания прямоугольника с единичной высотой, площадь которого равно площади, ограниченной кривой В_хх.

РАЗЛОЖЕНИЕ СИГНАЛОВ НА ЭЛЕМЕНТАРНЫЕ СОСТАВЛЯЮЩИЕ.

Реальные сигналы носят случайные характер и имеют сложную форму

1. Элементарные сигналы должны быть взаимно независимыми, и будучи умноженными на а_к, мы должны получить S(t).

2. Значения весовых коэффициентов а_к не должны зависеть от количества элементных составляющих.

Этим двум требованиям отвечает ортогональная функция.

Лекция-33 РАЗЛОЖЕНИЕ СИГНАЛА В ТРИГОНОМЕТРИЧЕСКИЙ РЯД ФУРЬЕ.

(1)

(2) (3)

(4) (5)

ЭНЕРГЕТИЧЕСКИЙ СПЕКТР СИГНАЛА.

Пусть S(t) носит случайный характер.

- текущий спектр для сигнала длительности Т.

Спектральная плотность мощности: 1. Формулы Винер-Хинчена

Эти формулы связывают функцию корреляции с энергетическим спектром.

Если В(τ) четная функция, тогда

ПРОХОЖДЕНИЕ СЛУЧАЙНЫХ СИГНАЛОВ (ПРОЦЕССОВ) ЧЕРЕЗ РАДИОТЕХНИЧЕСКОЕ ЗВЕНО

Лекция-34 ПРОХОЖДЕНИЕ СЛУЧАЙНОГО СИГНАЛА ЧЕРЕЗ ЛЭЦ

При прохождении случайных процессов (сигналов), через линейные радиотехнические устройства в общем случае изменяются все числовые характеристики отклика (математическое ожидание, дисперсия ...) Только в одном случае, когда входной процесс (сигнал) подчиняется нормальному закону распределения, то и отклик Y(t) подчиняется нормальному закону распределения.

Если входной сигнал имеет спектр Δω_сп >>ω_эфф или Δω_пплс , то про­исходит нормализация закона распределения отклика, т.е. отклик будет подчиняться нормальному закону распределения. Согласно центральной предельной теореме. По теореме вероятности: сумма больше числа слу­чайных величин подчиняется нормальному закону распределения.

Флуктуационными помеху называют узкополосной, если интервал корреляции Δτ > t_уст переходных процессов линейной системы. Если помеха широкополосная, то функция корреляции

Флуктуационную помеху называют гладкой или помехой белого шума.

Сигнал по КС передается по AM g = С/П