
- •Курсовая работа
- •Оглавление
- •Глава 1 4
- •Глава 2 29
- •Введение
- •Глава 1
- •1.1 Бинарные отношения
- •1.2 Операции над отношениями
- •1.3 Свойства отношений
- •1.4 Инвариантность отношений
- •1.5 Отношение эквивалентности
- •1.6 Классы эквивалентности
- •Глава 2
- •2.1 Основные определения
- •2.1 Операции над нечеткими множествами
- •Заключение в этой работе были рассмотрены:
- •2) Операции над отношениями:
- •Приложения
- •Литература
Глава 2
2.1 Основные определения
Теория нечетких множеств представляет собой обобщение и переосмысление важнейших направлений классической математики. У ее истоков лежат идеи и достижения многозначной логики, которая указала на возможности перехода от двух к произвольному числу значений истинности и поставила проблему оперирования понятиями с изменяющимся содержанием; теории вероятностей, которая, породив большое количество различных способов статистической обработки экспериментальных данных, открыла пути определения и интерпретации функции принадлежности; дискретной математики, которая предложила инструмент для построения моделей многомерных и многоуровневых систем, удобный при решении практических задач.
Подход
к формализации понятия нечеткого
множества состоит в обобщении понятия
принадлежности. В обычной теории множеств
существует несколько способов задания
множества. Одним из них является задание
с помощью характеристической функции,
определяемой следующим образом. Пусть ![]() —
так называемое универсальное множество,
из элементов которого образованы все
остальные множества, рассматриваемые
в данном классе задач, например множество
всех целых чисел, множество всех гладких
функций и т.д. Характеристическая функция
множества
—
так называемое универсальное множество,
из элементов которого образованы все
остальные множества, рассматриваемые
в данном классе задач, например множество
всех целых чисел, множество всех гладких
функций и т.д. Характеристическая функция
множества ![]() —
это функция
—
это функция ![]() ,
значения которой указывают, является
ли
,
значения которой указывают, является
ли ![]() элементом
множества A:
элементом
множества A:
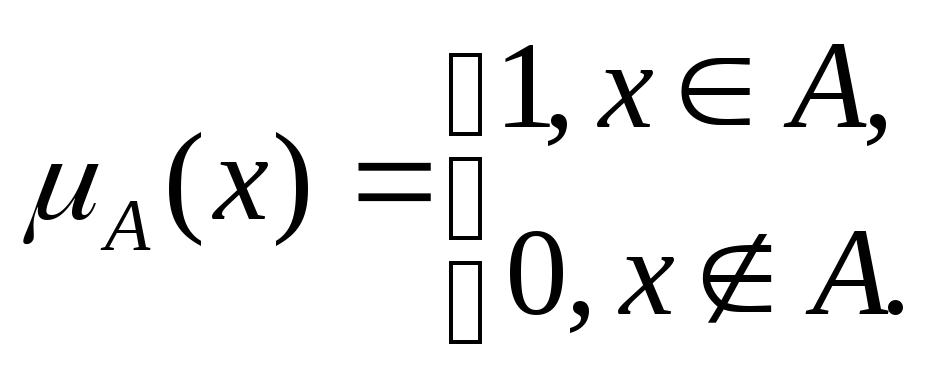
Особенностью этой функции является бинарный характер ее значений.
С точки
зрения характеристической функции, нечеткие
множества есть
естественное обобщение обычных множеств,
когда мы отказываемся от бинарного
характера этой функции и предполагаем,
что она может принимать любые значения
на отрезке [0,1].
В теории нечетких
множеств характеристическая
функция называется функцией
принадлежности,
а ее значение ![]() — степенью
принадлежности элемента x нечеткому
множеству A.
— степенью
принадлежности элемента x нечеткому
множеству A.
Более строго, нечетким множеством A называется совокупность пар
![]()
Где
![]() —
функция принадлежности, т.е.
—
функция принадлежности, т.е.
![]() .
.
Пусть,
например,
![]()
![]()
Будем говорить, что элемент a не принадлежит множеству A, элемент b принадлежит ему в малой степени, элемент c более или менее принадлежит, элемент d принадлежит в значительной степени, e является элементом множества A.
Пример. Пусть
универсум U есть
множество действительных чисел. Нечеткое
множество A,
обозначающее множество чисел, близких
к 10 (см. рис.1.1), можно задать следующей
функцией принадлежности:![]() ,
где
,
где ![]() .
.
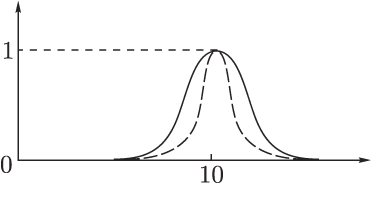
Рис. 1.1.
Показатель
степени m выбирается
в зависимости от степени близости к 10.
Например, для описания множества чисел,
очень близких к 10, можно положить
![]() ;
для множества чисел, не очень далеких
от 10,
;
для множества чисел, не очень далеких
от 10, ![]() .
.
Пример. Коротко остановимся на понятии лингвистической переменной (более детальное изучение будет в последующих лекциях). Лингвистическую переменную можно определить как переменную, значениями которой являются не числа, а слова или предложения естественного (или формального) языка. Например, лингвистическая переменная "возраст" может принимать следующие значения: "очень молодой", "молодой", "среднего возраста", "старый", "очень старый" и др. Ясно, что переменная "возраст" будет обычной переменной, если ее значения — точные числа; лингвистической она становится, будучи использованной в нечетких рассуждениях человека.
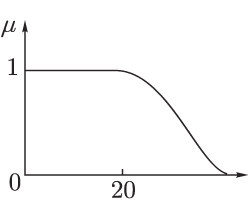 Рис.
1.2.
Рис.
1.2.
Каждому значению лингвистической переменной соответствует определенное нечеткое множество со своей функцией принадлежности. Так, лингвистическому значению "молодой" может соответствовать функция принадлежности, изображенная на рис. 1.2
