4.10.3. Запись функции в виде сднф и скнф

Возьмем функцию двух переменных x₁x₀. Применим к ней терему разложения для переменной x₁.

Далее каждую из функций и разложим по переменной x₀.

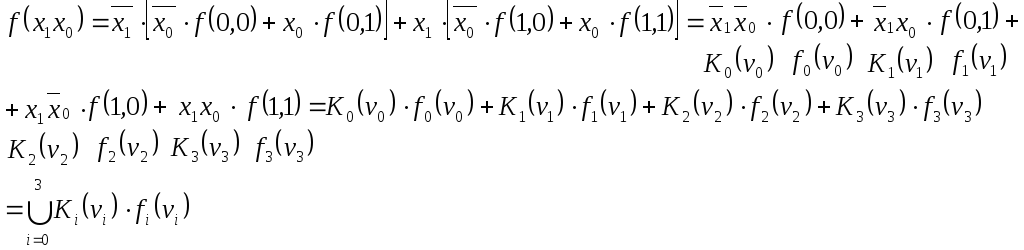
Такая форма представления функции называется совершенной дизъюнктивной нормальной формой (СДНФ).

В общем виде представление функции в СДНФ:

Так как значение функции то если и если отсюда СДНФ можно представить в виде:

где i₁ – номера точек, в которых функция .

СДНФ можно получить аналогичным способом с помощью теоремы разложения. Но можно пойти более легким путем.

Возьмем инверсию СДНФ: из данного соотношения на основании закона двойственности получим: а так как общий вид СКНФ:

Так как значение функции то если и если отсюда СКНФ можно представить в виде:

где i₀ – номера точек, в которых функция .

4.10.4. Совершенные нормальные формы в базисах и-не и или-не

Совокупность элементарных функций, с помощью которых можно записать любую функцию , называется функционально полной системой функций или базисом. Из выше приведенного параграфа можно сделать вывод, что для представления любой функции , в СДНФ и СКНФ достаточно использовать только функции (операции) И, ИЛИ и НЕ, т.е. совокупность этих функций является базисом.

Преобразуем СДНФ функции с помощью законов двойного отрицания и де Моргана:

Данная форма представления функции называется совершенной нормальной формой (СНФ) в базисе И-НЕ, так как она требует использования только функций (операций) И-НЕ.

Проведем аналогичные действия с СКНФ:

Данная форма представления функций называется СНФ в базисе ИЛИ-НЕ, так как она требует использования только функций (операций) ИЛИ-НЕ.

4.11. Минимизация логических функций

Одной из основных задач, возникающих при синтезе комбинационных схем (КС), является минимизация логических функций, которые эти КС реализуют. Чем проще логическое выражение, описывающее функцию, тем проще и дешевле реализующая ее КС.

В качестве критерия сложности логического выражения, описывающего функцию, целесообразно принять числи первичных термов , в него входящих.

Существуют два метода минимизации:

аналитический, весьма трудоемок и требует не тривиального подхода, который не всегда виден;

графический, наиболее нагляден, прост в использовании, но может иметь некоторые ограничения.

Очевидно, что любой метод минимизации может основываться только на тождественном преобразовании логических выражений.

4.11.1. Конъюнктивные и дизъюнктивные термы

Конъюнктивным термом (контермом) называется: конъюнкция любого числа первичных термов, если каждый первичный терм с индексом p входит в него не более одного раза.

- функция представляет собой конъюнкцию первичных термов.

Дизъюнктивным термом (дизтермом) называется: дизъюнкция любого числа первичных термов, если каждый первичный терм с индексом p входит в нее не более одного раза.

- функция представляет собой дизъюнкцию первичных термов.

Пример: Возьмем две точки области определения функции трех переменных i=1₁₀ (001)₂и j=5₁₀ (101)₂. Выразим эти точки через термы .

Для точки i -

Для точки j -

1. Сложим первичные термы с одинаковыми индексами точки i и точки j соответственно.

, , - перемножим полученные результаты получим: - контерм точек 1 и 5 области определения функции трех переменных.

2. Перемножим первичные термы с одинаковыми индексами точки i и точки j соответственно, при этом проведем инверсию каждого терма, , , сложим полученные результаты, получим: - дизтерм точек 1 и 5 области определения функции трех переменных.