
методические указания по лабораторным работам / РАСЧЕТ СИСТЕМЫ УПРАВЛЕНИЯ ПОЗИЦИОНИРОВАНИЕМ ЭЛЕКТРОПРИВОДА В РЕЖИМЕ МАЛЫХ ПЕРЕМЕЩЕНИЙ
.docМинистерство образования и науки Российской федерации
Федеральное агентство по образованию
Саратовский государственный технический университет
Балаковский институт, техники, технологии и управления
РАСЧЕТ СИСТЕМЫ УПРАВЛЕНИЯ ПОЗИЦИОНИРОВАНИЕМ ЭЛЕКТРОПРИВОДА В РЕЖИМЕ МАЛЫХ ПЕРЕМЕЩЕНИЙ
Методические указания к выполнению практической работы
по дисциплине «Электромеханические системы» для студентов
специальности 210100 всех форм обучения
Одобрено
редакционно-издательским советом
Балаковского института техники,
технологии и управления
Балаково 2009
ВВЕДЕНИЕ
Управление положением находит широкое применение в станках с ЧПУ, в системах наведения антенн, телескопов, в системах управления промышленными роботами и в большинстве случаев строятся по принципу подчиненного регулирования. Системы управления положением принято разделять на работающие в режиме позиционирования и слежения. Позиционированием называется такой режим работы, при котором задачей управления является перемещение электроприводом механизма (рабочего органа) из одного положения в другое при требуемом быстродействии.
В режиме позиционирования различают:
- режим малых перемещений, при котором ни один из регуляторов не ограничен и система работает как линейная;
- режим средних перемещений, при котором ограничен якорный ток, т.е. ограничен выходной сигнал регулятора скорости;
- режим больших перемещений, при обработке которых двигатель в течении некоторого времени работает на установившейся скорости, т.е. все регуляторы некоторое время находятся в зоне ограничения.
Цель работы: аналитический расчет параметров следящей трехконтурной системы в режиме малых перемещений с установлением связей между параметрами регуляторов и основными показателями качества переходных процессов.
ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
На рис.1 изображена структурная схема трехконтурной системы, работающей в режиме малых перемещений. В режиме малых перемещений ни один из регуляторов не входит в насыщение и поэтому система линейна. Оптимизация контура положения начинается с внутреннего контура тока. Он настраивается на технический оптимум с малой некомпенсируемой постоянной времени ТμТ=Тμ+0,5·ТДТ.

Рис.1. Структурная схема трехконтурной системы
Если не учитывать инерционность датчика тока, то некомпенсированная постоянная времени внутреннего контура в первом приближении определяется инерционностью тиристорного преобразователя ТμТ=Тμ=ТП.
Передаточная функция контура тока, настроенного на технический оптимум, имеет вид
|
|
(1) |
Используя параметры структурной схемы внутреннего контура тока
|
|
(2) |
Приравнивая выражения (1) и (2) получим выражение для расчета передаточной функции регулятора тока:
|
|
(3) |
Получаем, что регулятор тока состоит из параллельного соединения усилительного и интегрирующего звена, т.е. является пропорционально-интегральным (ПИ-регулятором).
Передаточная функция замкнутого контура тока после упрощения
|
|
(4) |
Так как ТμТ малая величина (ТμТ<<1), можно приближенно записать:
|
|
(5) |
Структурная схема с оптимизированным контуром тока представлена на рис.2.

Рис.2. Структурная схема трехконтурной системы с оптимизированным
контуром тока
Используя структурную схему рис.2, осуществим настройку контура скорости на технический оптимум. В этом случае некомпенсируемой постоянной является постоянная времени ТμС=2ТμТ+0,5·ТДС. Аналогично без учета инерционности обратной связи ТμС=2ТμТ=2Тμ.
Используя параметры структурной схемы внутреннего контура тока
|
|
(6) |
Откуда передаточная функция регулятора скорости:
|
|
(7) |
В выражение (7) использовалась подстановка:
|
|
(8) |
Получаем, что регулятор скорости состоит из усилительного звена, т.е. является пропорциональным (П-регулятором).
Настроив контур скорости на технический оптимум, получим передаточную функцию замкнутого контура скорости
|
|
(9) |
На рис.3 представлена структурная схема трехконтурной системы с оптимизированным контуром скорости

Рис.3. Структурная схема трехконтурной системы с оптимизированным
контуром скорости
Некомпенсируемой постоянной времени контура положения является постоянная ТμП=2ТμС+0,5·ТДП. Без учета инерционности фильтра в цепи обратной связи ТμП=2ТμС=4ТμТ.
Осуществим настройку контура положения на технический оптимум и определим параметры регулятора положения
|
|
(10) |
|
|
|
|
(11) |
||
Получаем, что регулятор положения состоит из усилительного звена, т.е. является пропорциональным (П-регулятором).
При пропорциональном регуляторе скорости точная обработка задающего сигнала будет осуществляться только при отсутствии нагрузки. Для точной обработки входного сигнала при наличии нагрузки следует применить пропоционально-интегральный регулятор скорости, т.е. настроить контур скорости на симметричный оптимум.
Желаемая передаточная функция разомкнутого контура с настройкой на симметричный оптимум:
|
|
(12) |
Используя параметры структурной схемы контура скорости, имеем
|
|
(13) |
Из выражения (13) передаточная функция регулятора скорости:
|
|
(14) |
С учетом обозначения (8)
|
|
(15) |
При применении ПИ-регулятора в системе возрастет перерегулирование, для исключения которого на вход регулятора скорости ставится фильтр (апериодическое звено) с постоянной времени 4ТμС:
|
|
(16) |
С применением фильтра передаточная функция замкнутого скорости с пропорционально-интегральным регулятором имеет вид
|
|
(17) |
Приняв, что Т’μП=4ТμС+0,5·ТДП, получаем структурную схему контура положения (аналогично схеме рис.3), где вместо постоянной ТμП используется постоянная Т’μП. Параметры регулятора положения в случае применения фильтра и ПИ-регулятора скорости определяются согласно (11)
|
|
(18) |
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Ознакомиться с теоретическим материалом.
2. На основании исходных данных рассчитать недостающие параметры.
3. На основании исходных данных рассчитать все параметры регуляторов.
4. Рассчитать передаточные функции замкнутой системы позиционирования, построить переходные процессы и сделать выводы.
5. Составить отчет по работе.
ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАНИЯ
Параметры двигателя:
- номинальная частота вращения nН=1030 об/мин;
- сопротивление якоря RЯ=1,14 Ом;
- индуктивность якоря LЯ=0,014 Гн;
- момент инерции J=0,125 кг·м2;
- номинальное напряжение UН=220 В;
- номинальный момент МН=45,9 Н·м;
- номинальный ток IН=26 А;
- перегрузочная способность двигателя λ= IMAX/ IН=2,5.
1) Рассчитаем недостающие параметры.
Номинальная угловая скорость
![]() ,
рад/с.
,
рад/с.
Коэффициент ЭДС kЕ:
![]() ,
В·с.
,
В·с.
Коэффициент момента kМ:
![]() ,
Н·м А-1.
,
Н·м А-1.
Электромагнитная постоянная времени двигателя:
![]() с.
с.
Механическая постоянная времени двигателя:
![]() с.
с.
Вспомогательный коэффициент k0:
![]() ,
А/В.
,
А/В.
Величины коэффициентов усиления датчиков тока kДТ и скорости определяются выражениями
![]() ,
,
![]() ,
,
где Umax максимально допустимое выходное напряжение регуляторов. Исходя из того, что большинство операционных усилителей питаются напряжением ±12 В, принимаем Umax=10В. Тогда
![]() ,
,
![]() ,
,
Принимаем, что двигатель получает питание от трехфазного тиристорного преобразователя, собранного по схеме Ларионова, тогда некомпенсированная постоянная времени будет определяться по формуле:
![]() ,
,
где f=50 Гц – частота питающей сети;
m=6 – число пульсов за период.
![]() с.
с.
При переходе от тиристорной схемы к транзисторной – запаздывание Тμ может быть уменьшено.
Определим коэффициент передачи тиристорного преобразователя из следующих соображений. Если принять, что максимальный выход регулятора 10В обеспечивает подачу на двигатель 220В, то коэффициент передачи выпрямителя будет равен
![]() .
.
2) Рассчитаем передаточные функции регуляторов.
Передаточная функция регулятора тока согласно (3):
![]() .
.
Передаточная функция регулятора скорости, настроенного на технический оптимум согласно (7):
![]() .
.
Передаточная функция регулятора положения, принимая kДП=1, согласно (11)
![]() .
.
Передаточная функция регулятора скорости, настроенного на симметричный оптимум согласно (15):
![]() .
.
Передаточная функция регулятора положения, с учетом настройки контура скорости на симметричный оптимум согласно (18):
![]() .
.
3) Передаточная функция замкнутой трехконтурной системы, на основании рис.3 без учета инерционности датчика положения имеет вид:
 .
.
С учетом численных значений передаточная функция замкнутой системы при настройке контура скорости на технический оптимум имеет вид
![]()
При настройке контура скорости на симметричный оптимум соответственно
![]() .
.
На рис.4 представлены
переходные процессы системы ( 1 – с
настройкой контура скорости на технический
оптимум, 2 – с настройкой контура скорости
на симметричный оптимум) без учета
нагрузки.

Рис.4. Переходные процессы трехконтурной системы
На основании данных графиков можно сделать следующие выводы:
- система позиционирования отрабатывает задающее воздействие при обоих способах настройки контура тока за одинаковое время t=0,15 с;
- перерегулирование в системе при настройке контура тока на симметричный оптимум уменьшается в ≈1,7 раз по сравнению с настройкой на технический оптимум.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Чем характеризуются режимы систем регулирования положением?
2. Как определяются малые некомпенсируемые постоянные времени каждого контура?
3. Как определяются параметры регуляторов контура тока, скорости и положения, если они настроены на технический оптимум?
4. Как определяются параметры регулятора контура скорости, если он настроен на симметричный оптимум?
5. Как изменяться характеристики трехконтурной системы после настройки контура скорости на симметричный оптимум?
ВАРИАНТЫ ЗАДАНИЙ
-
№
UН
IН
МН
nН
RЯ
LЯ
J
λ
1
60
2,86
0,39
3000
0,46
0,02
15,3·10-4
25
2
60
2,27
0,49
2000
0,94
0,038
15,3·10-4
50
3
110
1,53
0,39
3000
1,48
0,069
15,3·10-4
25
4
110
1,22
0,49
2000
3,0
0,129
15,3·10-4
50
5
60
4,57
0,65
3000
0,23
0,013
20,4·10-4
25
6
60
2,72
0,585
2000
0,52
0,032
20,4·10-4
50
7
110
2,46
0,65
3000
0,765
0,043
20,4·10-4
25
8
110
1,46
0,585
2000
1,74
0,108
20,4·10-4
50
9
60
5,6
0,81
3000
0,284
0,01
35,7·10-4
25
10
60
4,3
0,97
2000
0,645
0,02
35,7·10-4
50
11
110
3,05
0,91
3000
0,945
0,034
35,7·10-4
25
12
110
2,33
0,97
2000
2,2
0,068
35,7·10-4
50
13
110
8,2
2,96
2500
0,237
0,015
135·10-4
25
14
110
5,0
2,92
1500
0,605
0,042
135·10-4
50
15
220
4,1
2,96
2500
0,85
0,061
135·10-4
25
16
220
2,5
2,92
1500
2,38
0,168
135·10-4
50
17
110
19,2
6,25
2500
0,147
0,006
408·10-4
25
18
110
13,0
7,15
1500
0,42
0,016
408·10-4
50
19
220
9,5
6,25
2500
0,58
0,066
408·10-4
25
20
220
6,4
7,15
1500
1,7
0,027
408·10-4
50
21
110
36,6
12,5
2500
0,06
0,003
662·10-4
25
22
110
18,2
10,4
1500
0,192
0,012
662·10-4
50
23
220
12,6
10,7
2500
0,435
0,014
662·10-4
25
24
220
18,2
12,5
1500
0,239
0,023
662·10-4
50
25
220
27,2
19,4
2500
0,39
0,009
127·10-4
50
ВРЕМЯ, ОТВЕДЕННОЕ НА ВЫПОЛНЕНИЕ РАБОТЫ
1. Подготовка к работе – 1,0 акад.час
2. Выполнение работы – 1,0 акад.часа
3. Оформление работы – 1,0 акад.час
ЛИТЕРАТУРА
1. Терехов В.М. Системы управления электроприводов: учебник для студентов высш.учеб.заведений / В.М.Терехов, О.И.Осипов; под ред. В.М.Терехова. – 2-е изд., стер. – М.: «Академия», 2006. – 304с.
2. Соседка В.Л. Локальные системы автоматики и следящий электропривод: учеб.пособие для студ. высш.учеб.заведений / В.Л.Соседка. – Днепропетровск: НГУ, 2003. – 144 с.
РАСЧЕТ СИСТЕМЫ УПРАВЛЕНИЯ ПОЗИЦИОНИРОВАНИЕМ ЭЛЕКТРОПРИВОДА В РЕЖИМЕ МАЛЫХ ПЕРЕМЕЩЕНИЙ
Методические указания к выполнению практической работы
по дисциплине «Электромеханические системы» для студентов
специальности 210100 всех форм обучения
Составили: Мефедова Юлия Александровна
Рецензент Т.Н. Скоробогатова
Редактор Л.В.Максимова
Корректор А.М.Рогачева
|
Подписано в печать |
|
Формат 60х84 1/16 |
|
Бумага тип. |
Усл. печ. л. 0,75 |
Уч.-изд.л. 0,625 |
|
Тираж 100 экз. |
Заказ |
Бесплатно |
Саратовский государственный технический университет
410054, г.Саратов, ул.Политехническая, 77
Копипринтер БИТТиУ,
413840, г.Балаково, ул. Чапаева, 140


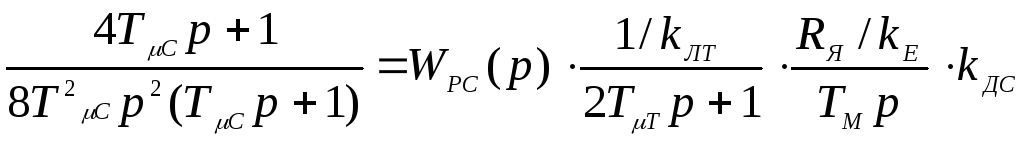 .
. .
.
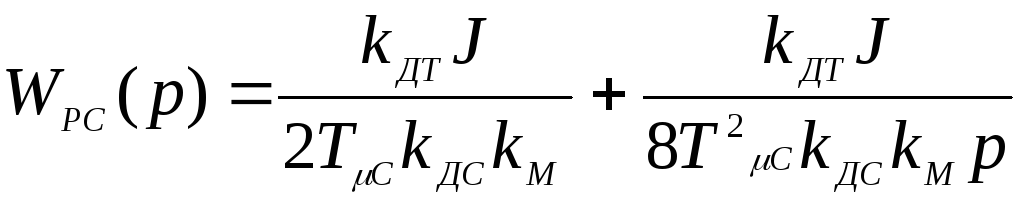 .
.