6 Передаточные функции двигателя постоянного тока

Рассмотрим двигатель независимого (параллельного) возбуждения с управлением за счет изменения напряжения на якоре. Для того, чтобы получить передаточную функцию необходимо составить дифференциальное уравнение, описывающее электрическую цепь двигателя в переходном процессе и дифференциальное уравнение движения вала двигателя (механика процесса). В переходном процессе обмотка якоря имеет две составляющие сопротивления: активную (обозначим ее здесь R_я) и реактивную, которая будет определяться величиной индуктивности обмотки L_я. Подводимое напряжение U уравновешивается ЭДС самоиндукции якоря ( ), падением напряжения на активном сопротивлении якоря (i_яR_я) и противо-эдс e_я, возникающей в якоре при вращении, тогда будет справедливо выражение вида

, (6.1)

где L_я – индуктивность якорной обмотки.

Для противо-эдс с большой степенью точности можно записать

е_я=k_эм. (6.2)

где k_эм=с_еФ – электромагнитный коэффициент

Дифференциальное уравнение движения вала двигателя имеет вид

, (6.3)

где J  момент инерции вращающихся частей, приведенный к валу двигателя,

М_с  статический момент или момент сопротивления (в общем случае равен сумме нагрузочного момента и момента трения двигателя).

На первом этапе будем считать , что статическим моментом можно пренебречь (т.е. пусть М_с=0), тогда получим

, (6.4)

где k_эм=с_мФ – электромагнитный коэффициент.

Величина тока якоря тогда, находится по формуле

. (6.5)

Подставим выражения 5.3 и 5.6 в исходное дифференциальное уравнение электрической цепи и получим

. (6.6)

Теперь обе части уравнения 5.7 разделим на k_эм, а коэффициент при второй производной разделим и умножим на R_я. Уравнение примет вид

. (6.7)

Введем следующие обозначения:

- электромеханическая постоянная времени двигателя,

- электромагнитная постоянная времени якоря двигателя.

Теперь, с учетом принятых обозначений можем записать

. (6.8)

Для получения передаточной функции нужно данное уравнение записать относительно изображений по Лапласу входного напряжения и угловой скорости на выходе двигателя

. (6.9)

Так как передаточная функция представляет собой отношение изображений выходной и входной величин, то можно записать

, (6.10)

где k_дв=1/k_эм – коэффициент передачи двигателя.

В зависимости от соотношения величин постоянных времени двигателя, вид его передаточной функции можно изменять. Так, если 4Т_я>Т_м, что встречается достаточно редко, двигатель описывается колебательным звеном. Чаще всего 4Т_я<Т_м и передаточную функцию можно представить в виде

. (6.11)

При анализе систем автоматического управления с двигателем постоянного тока часто пренебрегают электромагнитной постоянной, ввиду ее малости (Т_я0), по сравнению с другими постоянными времени системы, и используют передаточную функцию вида

. (6.12)

Кроме того, если выходной величиной является не угловая скорость, а угол поворота вала двигателя, которые, как известно, связаны соотношением, где(p)- изображение угла поворота вала двигателя, передаточная функция принимает вид

. (6.13)

При решении многих технических задач оказывается возможным пренебречь временем разгона (переходным процессом) по сравнению с полным временем вращения вала, и тогда двигатель может быть описан идеальным интегрирующим звеном

. (6.14)

Приведенные передаточные функции получены при условии равенства нулю статического момента. Можно показать, что они справедливы для М=const, если характеристики двигателя считать линейными. Величина М_с не влияет на постоянные времени и коэффициент передачи.

Для практических расчетов параметров передаточной функции двигателя, например, при синтезе систем управления, могут быть полезны следующие формулы:

(6.15)

где U_ном номинальное напряжение на якоре,

n_ном номинальная частота вращения [обороты/мин](задается в паспорте),

I_яном- номинальный ток якоря,

с_х – эмпирический коэффициент(0,4 – для машин без компенсационной обмотки, 0,1  с компенсационной обмоткой).

(6.16)

или

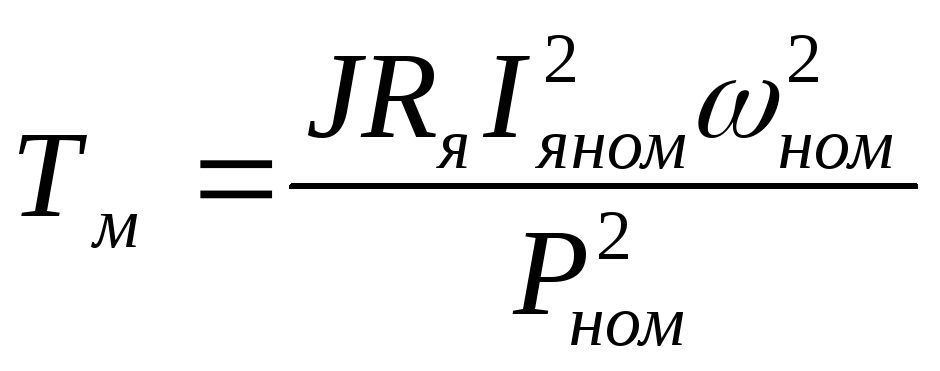. (6.17)

Необходимо также учитывать, что при введении добавочного сопротивления в цепь якоря постоянные времени изменяются, причем Т_я – уменьшается, а Т_м – растет. Если двигатель рассматривается совместно с механической нагрузкой и редуктором на его валу, то при расчетах Т_м нужно учитывать момент инерции редуктора и нагрузки приведенный к валу двигателя.

Для того, чтобы учесть влияние статического момента нагрузки М_с, удобнее воспользоваться методом структурного моделирования, используя те же базовые выражения 5.1 и 5.3. Считаем, что М_с=const, и его можно определить из выражения

, (6.18)

где i_с – ток якоря соответствующий статической нагрузке.

Уравнения 5.1 и 5.3 представим в форме:

, (6.19)

, (6.20)

где k_эм=с_мФ.

Тогда уравнение 5.19 можно записать относительно величины падения напряжения в якорной цепи

. (6.21)

В структурной схеме это может быть отражено с помощью апериодического звена первого порядка, на вход которого поступает разность между напряжением и ЭДС двигателя, а на выходе имеем падение напряжения в цепи якоря (Рисунок5.4).Уравнение 5.19 запишем в виде , а так как, то можно его записать относительно ЭДС в виде

. (6.22)

На структурной схеме данное уравнение будет представлено интегрирующим звеном с коэффициентом передачи , на выходе которого будем иметь напряжение равное противо-ЭДС двигателя е_я, а на входе разность падения напряжения на якоре и падения напряжения, определяемого током статической нагрузки (Рисунок5.4). Так как на выходе системы нужно иметь скорость вращения двигателя, то последовательно подключим безынерционное звено с коэффициентом передачи , гдеk_эм=с_еФ. А статический момент вводится как возмущающее воздействие через безынерционное звено с коэффициентом .

Для составления математических моделей двигателей смешанного и тем более последовательного возбуждения, которые обладают существенно нелинейными характеристиками, используют приближенные методы исследований, которые рассматриваются в теории автоматического управления, или специально разработанные в теории электропривода графоаналитические методы.