3. Кусочно-полиномиальная интерполяция

3.1. Локально-интерполяционные формулы

Разделим отрезок на частичных отрезков точками

.

Выберем на каждом - том отрезке , узлы интерполяции и построим для функции интерполяционный многочлен степени не выше :

,

где - номер частичного отрезка, - степень интерполяционного многочлена на отрезке .

Совокупность этих многочленов порождает на отрезке функцию , которую мы назовем локальным интерполянтом функции на отрезке :

. (3.1)

Таким образом, функция определена на всем отрезке и на каждом частичном отрезке совпадает с интерполяционным многочленом (склеена из многочленов, интерполирующих функцию на частичных отрезках). Функция не обязательно гладкая (даже непрерывная) в точках склейки интерполяционных многочленов. Этот способ приближения функции на отрезке называется локальной интерполяцией.

На каждом частичном отрезке погрешность локальной интерполяции для гладкой функции можно оценить с помощью формулы (1.13)

(3.2)

, .

Наиболее часто в практике используется локальная интерполянта для равноотстоящих узлов. Разделим отрезок на частичных отрезков равной длины точками

(3.3)

Выберем на каждом - том отрезке , узлы интерполяции

, . (3.4)

Здесь расстояние между любыми соседними узлами интерполяции равно

На каждом частичном отрезке построим для функции интерполяционный многочлен степени не выше :

. (3.5)

Построим на всем отрезке локальную интерполянту :

, .

Локальная интерполянта - склеена из многочленов , интерполирующих функцию на частичных отрезках. Функция непрерывна в точках склейки :

.

Замечание 3.1. Если общая степень интерполяционных многочленов не зависит от номера частичного отрезка , то в этом случае

параметром, за счет которого можно повышать точность приближения, является - число частичных отрезков.

При локальный интерполянт есть кусочно-линейная функция (ломаная) с вершинами в точках , при графиками многочленов на частичных отрезках будут параболы и так далее.

Если , то погрешность локальной интерполяции для () оценивается по формуле:

.

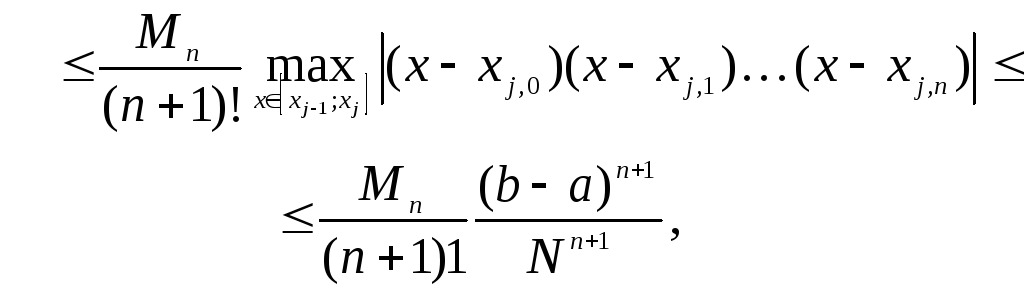
Отсюда получаем оценку погрешности для локальной интерполянты с равноотстоящими узлами (3.3)-(3.4):

(3.6)

.

Предложение 3.1. Для интерполяционный процесс, порожденный локальной интерполянтой для равноотстоящих узлов, определяемых формулами (3.3)-(3.4), равномерно сходится при к на :

на

со скоростью при .

Утверждение предложения 3.1. следует из оценки (3.6).

Теперь можно указать способ построения сходящегося интерполяционного процесса для любой непрерывной функции с помощью локальной интерполянты.

Теорема 3.1. Для любой функции интерполяционный процесс, порожденный локальной интерполянтой для равноотстоящих узлов, определяемых формулами (3.3)-(3.4), равномерно сходится при к на :

на

Доказательство. Введем оператор

, .

По построению - линейный ограниченный оператор в пространстве .

Теперь утверждение теоремы 3.1 означает, что последовательность операторов поточечно сходится при к единичному оператору , и нам нужно только проверить выполнение условий а) и б) теоремы 2.1 для последовательности при .

Выполнение условия б) теоремы 2.1 немедленно следует из предложения 3.1, так как множество плотно в .

Докажем справедливость условия б). Обозначим через - оператор интерполирования на отрезке , (см. (3.4)).

Имеем

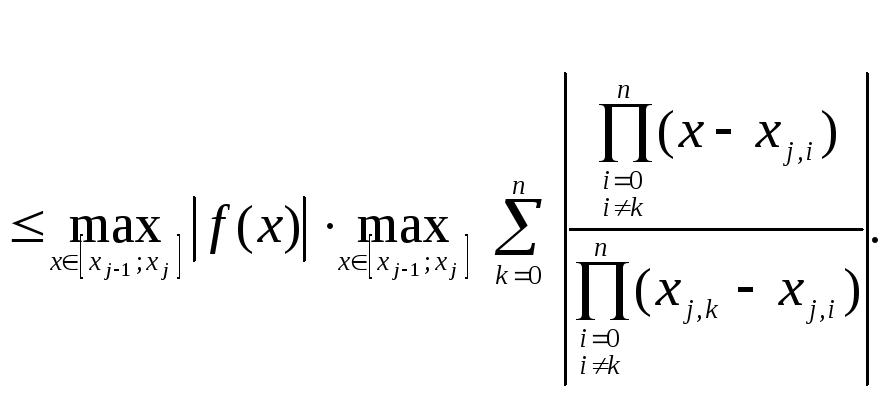(3.7)

Обозначив

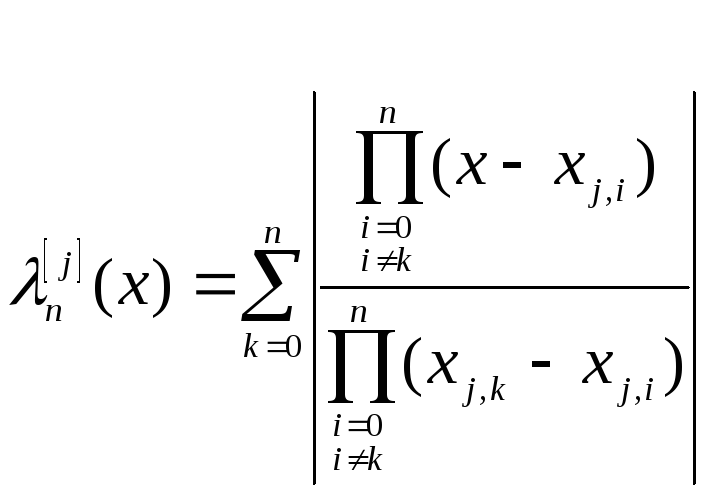, (3.8)

перепишем (3.7) в виде

(3.9)

Сделаем в (3.8) замену переменной, положив

Имеем

,

.

Подставляя найденные выражения в (3.7), получим функцию от новой переменной :

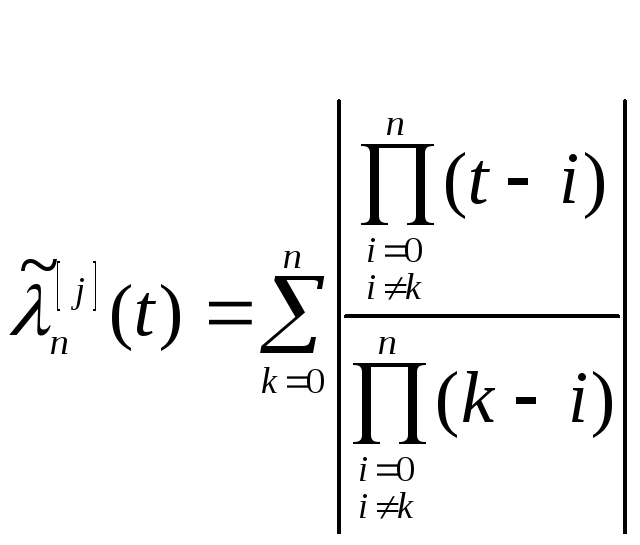. (3.10)

Так как функция 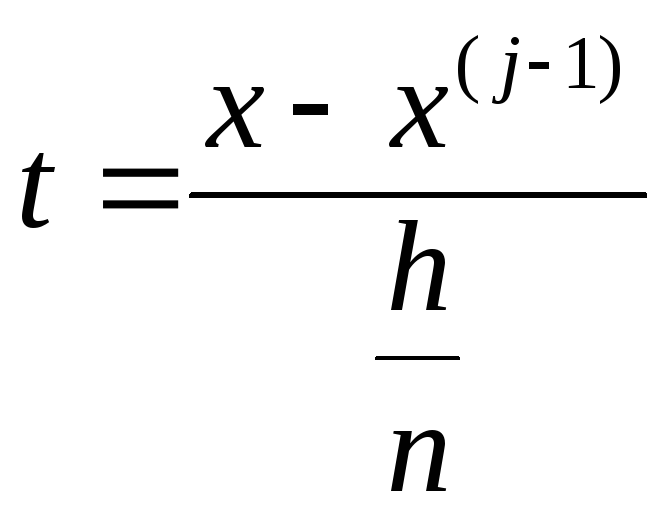взаимно однозначно отображает отрезок на отрезок , то

(3.11)

Отметим, что в (3.10) вычисляется максимальное значение функции , непрерывной на отрезке , независящей от и - номера отрезка . Следовательно,

(3.12)

зависит только от .

Используя (3.12), имеем

Отсюда для нормы оператора получим оценку:

. (3.13)

Условие a) теоремы 2.1 доказано. Так как не зависит от , то теорема 3.1 доказана.