1.6. Оптимальный выбор узлов интерполяции. Многочлены Чебышова

Формула (1.10) показывает, что погрешность интерполяции зависит от гладкости интерполируемой функции () и выбора узлов . Естественно возникает задача нахождения такого расположения узлов интерполяции на отрезке , при котором минимальна

величина и тем самым минимальна правая часть оценки погрешности интерполяции (1.12). Эта задача называется задачей об оптимальном выборе узлов интерполяции.

Замечание 1.11. Величина называется в конструктивной теории функций уклонением функции от нуля на отрезке .

Сначала найдем решение задачи об оптимальном выборе узлов интерполяции на отрезке . Для этого нам понадобятся многочлены Чебышова.

Многочлен Чебышова для определяется формулой

. (1.35)

Положим .

Покажем, что формула (1.35) действительно определяет многочлен степени с коэффициентом при старшей степени равным 1.

Используя формулу бинома Ньютона, имеем

,

.

Отсюда следует, что члены, содержащие иррациональности, при сложении взаимно уничтожаются. Получаем, что выражение (1.35) действительно является многочленом степени .

Так как,

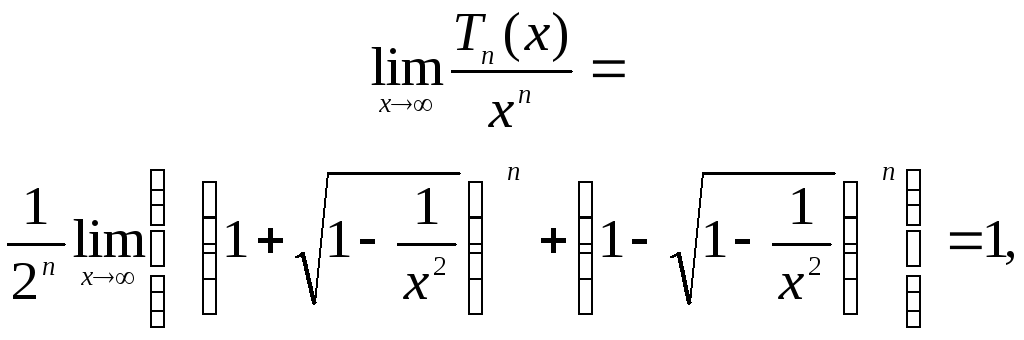
то коэффициент при старшей степени многочлена равен 1.

Многочлены Чебышова

Степень	Многочлен Чебышова

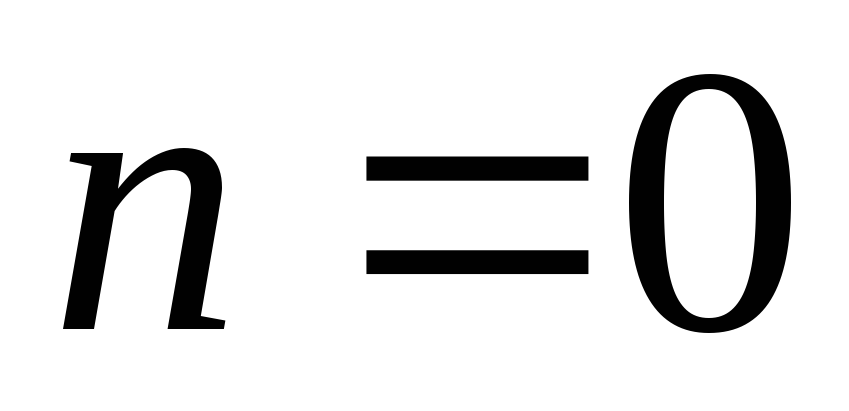
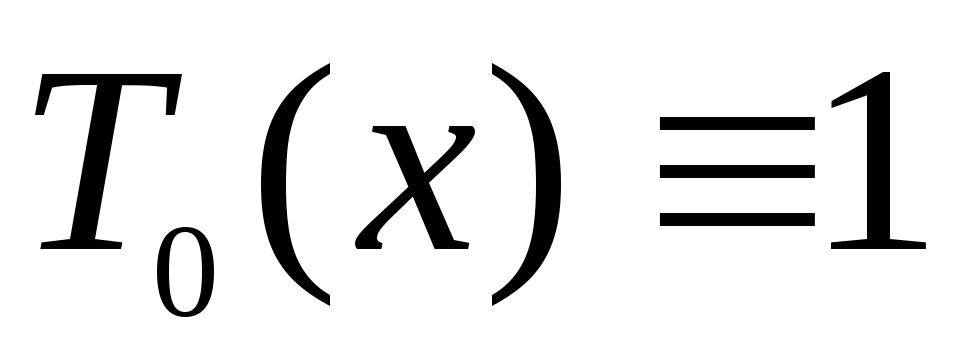
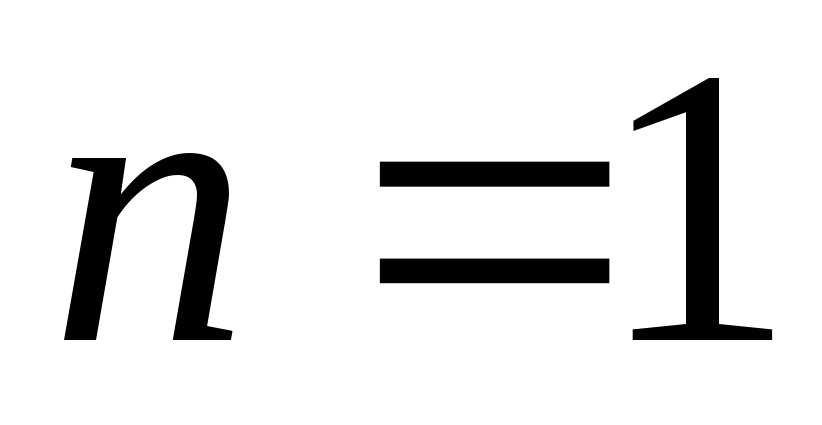
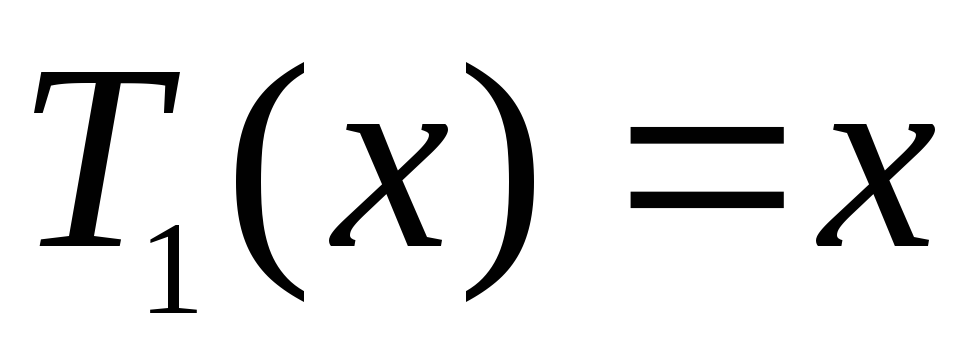
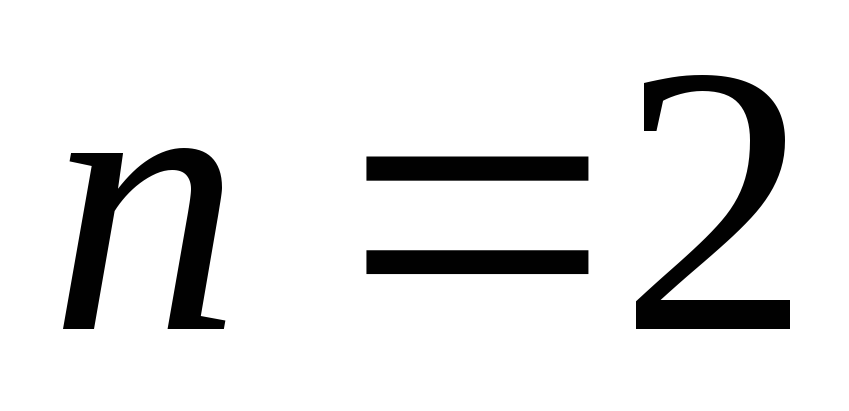
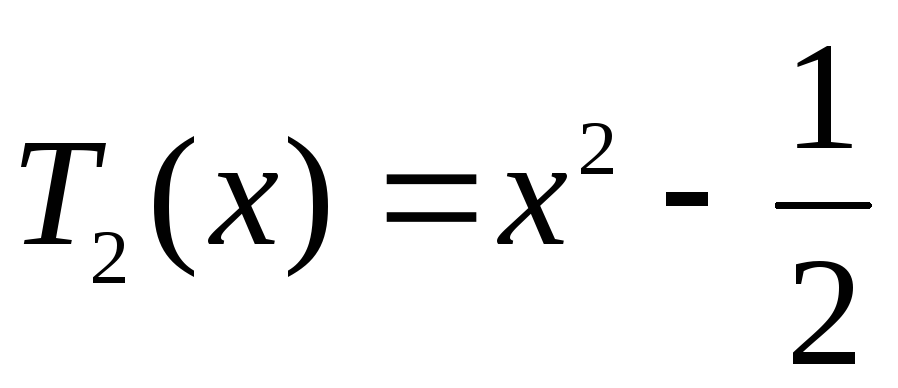
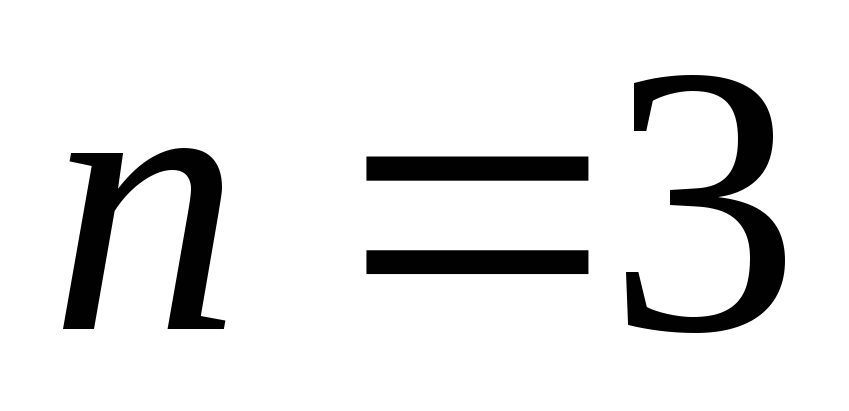
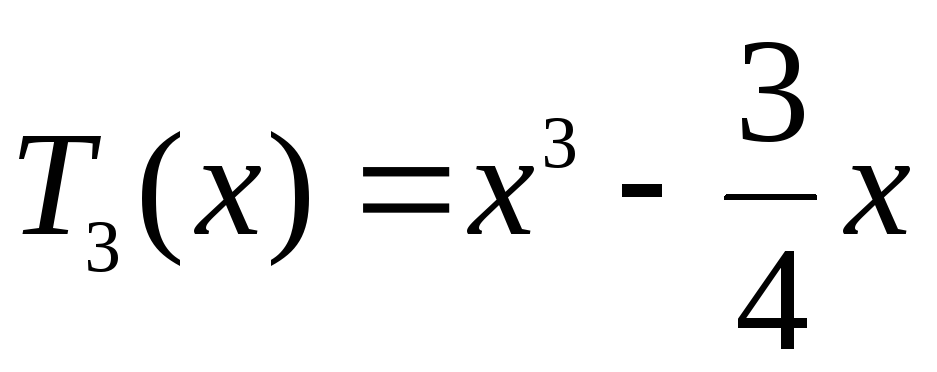
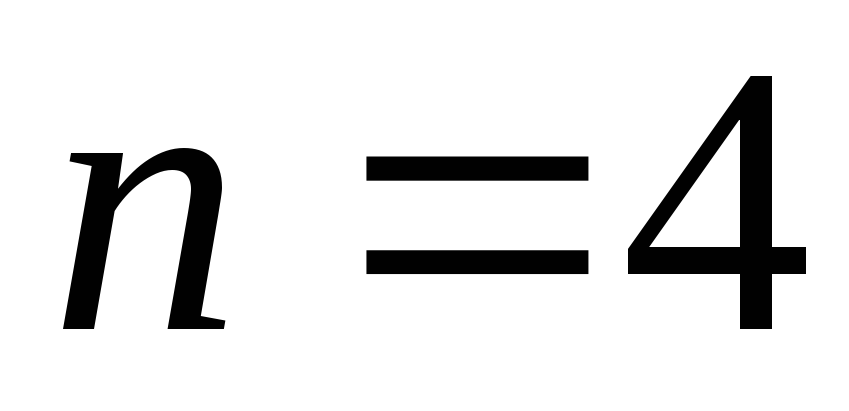
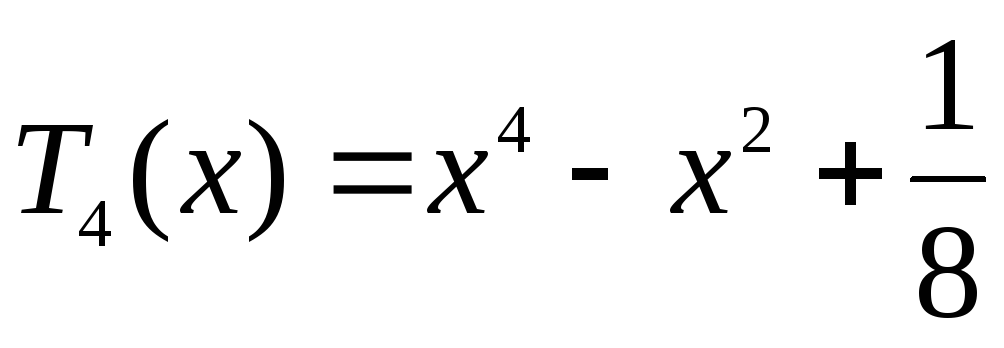
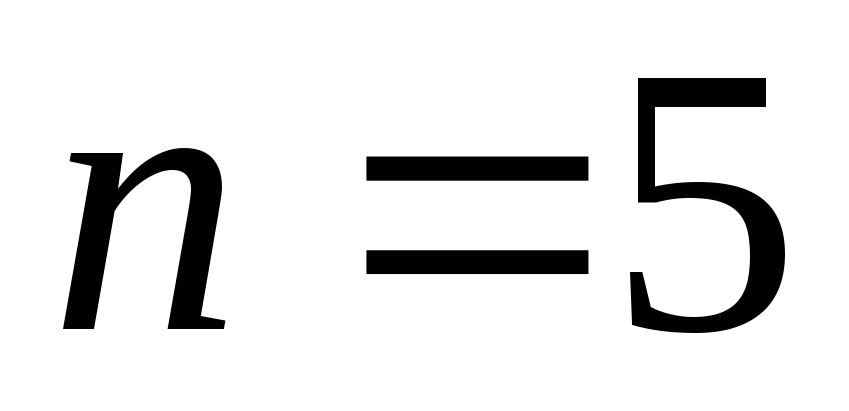
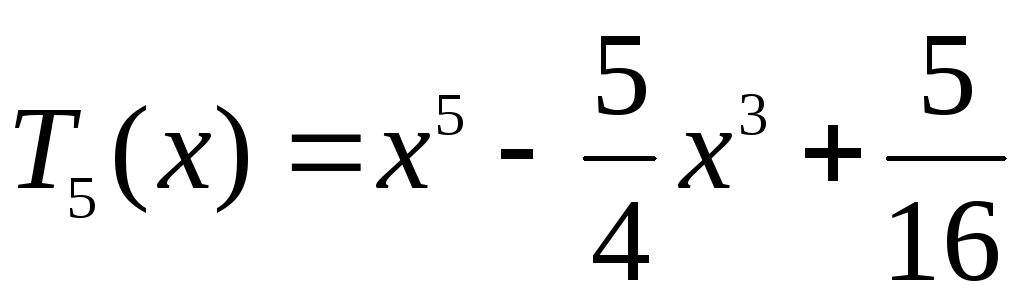
Рассмотрим поведение многочлена Чебышова на отрезке .

Положим в формуле (1.35) , (функция взаимно однозначно отображает отрезок на отрезок ).

Получим

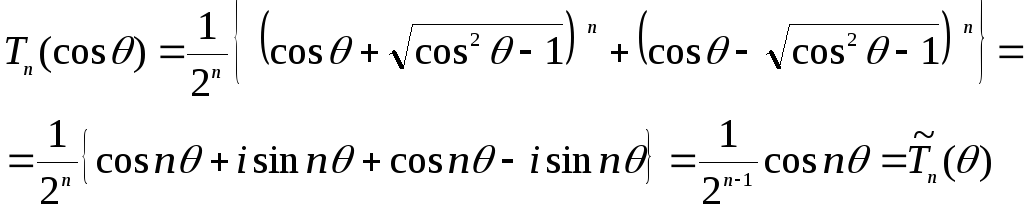
или

, (1.36)

Итак, значения многочлена при совпадают со значениями функции на отрезке .

Отсюда получаем, что

(1.37)

Предложение 1.3. Корни многочлена Чебышова , вещественные, различные и принадлежат интервалу .

Вопрос о корнях многочлена сводится к отысканию корней функции на отрезке .

Функция обращается в нуль в точках

, .

Отрезку принадлежат точки только при . Следовательно, все корней многочлена принадлежат интервалу и в силу (1.36) находятся по формуле

(1.38)

Предложение 1.3 доказано.

Замечание 1.12. Нули функции равномерно распределены на отрезке , расстояние между нулями равно . Корни многочлена Чебышова в силу нелинейности функции сгущаются к концам отрезка .

Предложение 1.4. Многочлен Чебышова , на отрезке имеет экстремумы

(1.39)

Действительно, производная обращается на отрезке в нуль в точках Точки находятся между нулями функции и, следовательно, являются точками экстремума. Отсюда получаем, что многочлен Чебышова имеет экстремумы при

Предложение 1.4 доказано.

Важное замечание 1.6. Многочлены Чебышова , на отрезке определяются формулой

. (1.40)

Формула (1.40) получается из (1.35) с помощью обратной замены при .

С помощью (1.40) легко вычисляются значения многочлена Чебышова на отрезке .

Замечание 1.13. Из формулы (1.40) немедленно получаем:

1) Все многочлены являются четными функциями, а нечетными.

2) Для имеет место рекуррентная формула

3) Многочлены , , образуют на отрезке ортонормированную систему функций с весом :

.

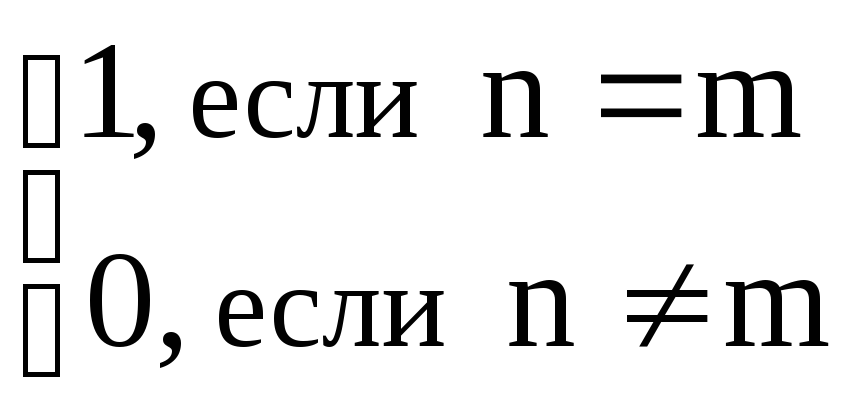Теорема 1.3. Многочлен Чебышова , среди всех многочленов степени с коэффициентом при старшей степени равным 1 имеет на отрезке наименьшее уклонение от нуля.

Это означает, что для любого многочлена , такого, что , имеем

(1.41)

Доказательство. Пусть существует многочлен , такой, что

, (1.42)

, .

Тогда разность будет многочленом степени не выше , отличным от тождественного нуля. Кроме того, в силу (1.37) и предположения (1.40) эта разность в точках принимает отличные от нуля значения противоположных знаков:

,

.

Это означает, что многочлен степени строго меньше обращается в нуль, по крайней мере, в точках (имеет различных корней), что невозможно.

Теорема 1.3 доказана.

Таким образом, для решения задачи об оптимальном выборе узлов интерполяции на отрезке в качестве узлов интерполяции нужно выбрать корни многочлена Чебышова , то есть точки

(1.43)

При этом в соответствии с (1.37) оценка погрешности интерполяции (1.12) примет вид

(1.44)

,

Из теоремы 3 следует, что оценку (1.41) улучшить на отрезке за счет другого выбора узлов интерполяции нельзя.

Рассмотрим случай интерполирования на произвольном отрезке Отрезок линейной заменой переменной

,

взаимно однозначно отображается на отрезок . При этом корням многочлена на отрезке соответствуют корни многочлена на отрезке :

,

. (1.43)

Точки (1.43) являются оптимальными узлами для оценки погрешности интерполяции на произвольном отрезке .

По узлам (1.43) построим :

Отсюда получаем оценку погрешности интерполяции на произвольном отрезке с узлами (1.43) в виде

(1.44)

.