1.5. Интерполяция с равноотстоящими узлами

Зададим узлы интерполяции , - шаг. Пусть и . Введем безразмерную независимую переменную . Имеем:

,

, .

Используя полученные выражения, запишем интерполяционный многочлен Лагранжа (1.7) в виде

, (1.22)

где

.

Далее

,

где

.

Теперь погрешность интерполяции (1.11) представляется формулой

, (1.23)

где та же самая, что и в формуле (1.10).

Заметим, если , то . В этом случае с учетом (1.13) и (1.23) имеем максимальную оценку погрешности интерполяции для равноотстоящих узлов

, (1.24)

где

,

.

Величина не зависит от . Ее можно заранее вычислить или оценить. В частности,

, , , , . (1.25)

Можно показать, что . Используя это неравенство, получаем из (1.24)

. (1.26)

Важное замечание 1.4. Из оценки (1.24) следует, что если число узлов таблицы (1.1) фиксировано , то при уменьшении максимальная погрешность интерполяции для равноотстоящих узлов ведет себя как . Отметим, что при уменьшении шага вдвое правая часть оценки (1.24) уменьшится по крайней мере в раза, так как .

Замечание 1.10. Для заданного узлы интерполяции целесообразно выбирать так, чтобы точка находилась как можно ближе к середине отрезка (Объясните почему?).

Если выполнено неравенство то формула (1.24) для погрешности интерполяции может быть уточнена.

В этом случае справедлива оценка

(1.27)

где

.

В частности,

, , , , . (1.28)

Сопоставляя (1.28) и (1.25), получаем, что оценка (1.27) для , удовлетворяющих условию является более точной, чем (1.24).

Для таблицы (1.1) с равноотстоящими узлами , введем в рассмотрение конечные разности функции .

Обозначим , . Величину

(1.29)

назовем конечной разностью первого порядка функции в точке

Конечной разностью второго порядка функции в точке назовем величину

(1.30)

Если известны конечные разности - ого порядка, то разделенная разность - ого порядка функции в точке определяется как

(1.31)

где

Для таблицы (1.1) можно построить таблицу конечных разностей:

Узлы	Конечные разности
	0-ого порядка	1-ого порядка	2-ого порядка			-ого порядка	-ого порядка
Число разностей						2	1

Из предложения 1.2 и его следствий получаем следующие основные свойства конечных разностей.

1) Конечная разность является линейным оператором относительно .

2) Для любого конечная разность вычисляется по формуле

где - коэффициенты бинома Ньютона.

3) Значение функции в точке (точка принадлежит множеству узлов таблицы (1.1), ) вычисляется по формуле

.

4) Разделенные разности и конечные разности связаны соотношением:

. (1.32)

5) Если , то

(1.33)

где .

Из формулы (1.33) следует, что конечные разности - го порядка от многочлена степени постоянны, а разности любого более высокого порядка равны нулю.

Используя связь (1.32) между разделенной разностью и конечной разностью и полагая , получим из интерполяционной формулы Ньютона (1.21) интерполяционный многочлен для равноотстоящих узлов ( , )

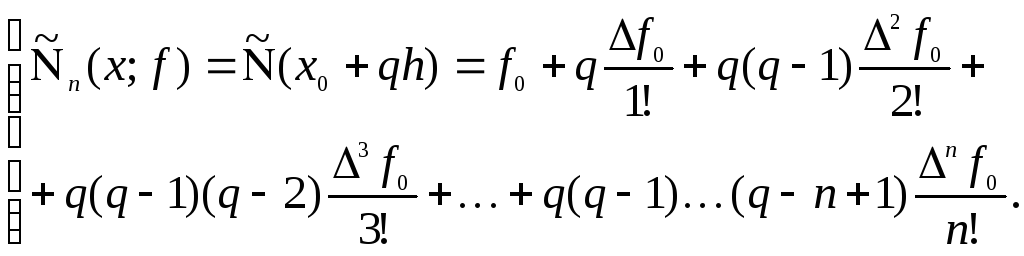(1.34)

Многочлен (1.34) называется интерполяционным многочленом Ньютона для равноотстоящих узлов для интерполяции вперед (первым интерполяционным многочленом Ньютона. Этот многочлен используется для вычисления значения функции в начале таблицы. Погрешность интерполяции здесь определяется формулой (1.21).

Важное замечание 1.5. Для таблицы (1.1) с равноотстоящими узлами, величину (конечную разность в точке ) можно отнести к различным точкам . В зависимости от точки, к которой ее относят, эту величину обозначают: - разность вперед, - разность назад, - центральная разность.

Таким образом,

.

Аналогично (1.31.) разности высших порядков определяют с помощью рекуррентных соотношений:

.

Используя разности назад и центральные можно построить специальные интерполяционные многочлены для вычисления значения функции в конце и середине таблицы (вторая интерполяционная формула Ньютона, интерполяционные формулы Гаусса, Стирлинга и Бесселя).