
4
.pdf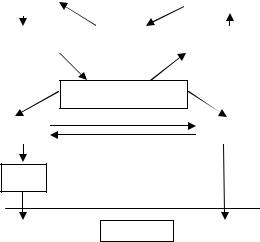
до вдыхания |
|
|
|
после вдыхания |
||
|
воздух |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
дыхательные пути
кровь |
|
жкт |
|
|
|
|
|
|
ткани
выделения
Рис. 17.3. Каналы распределения р/нв органах дыхания
Для количественной оценки характеристик процесса отложения частиц в дыхательных путях используются так называемые коэффициенты отложения или задержки, которые являются отношением числа частиц, отложившихся в легких, к полному числу вдыхаемых частиц. Данные о степени дисперсионности частиц позволяют определить место их отложения и вычислить активности в различных участках дыхательных путей.
Величина степени осаждения является сложной функцией различных факторов:
а) концентрацией аэрозолей; б) их физикохимическим состоянием; в) частотой и глубиной дыхания; г) размером частиц.
На рис. 17.4 представлена зависимость степени отложения вдыхаемых нуклидов от размеров частиц.
601
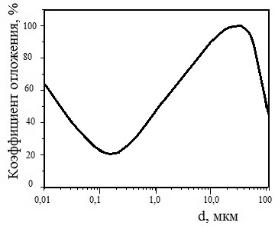
Рис. 17.4 Зависимость коэффициента отложения в органах дыхания аэрозольных частиц в зависимости от их размеров
При поступлении ингаляционным путем р/н с большим периодом полураспада частично поглощаются в самой легочной ткани, частично заглатываются и переходят в ЖКТ, откуда могут попасть в кровеносную систему. Часть нуклидов далее участвуют в нормальном обмене веществ и задерживаются в определенных системах организма или выводятся из него. Таким образом, облучению подвергаются не только органы дыхания, но и другие органы и ткани в соответствии с распределением веществ в организме.
3.3. Желудочно - кишечный тракт (ЖКТ, пероральный канал)
Вещества продуктов питания могут содержать фоновую активность различных р/н, а также могут быть загрязнены искусственными р/н, которые по биологическим цепочкам попадают в пищу. В пищеварительном тракте после соответствующих процессов они превращаются в химические соединения, используемые организмом. На основании физико-химических эффектов (диффузия, фильтрация, осмос) процесс всасывания описать трудно. Идут сложные биохимические превращения, когда, например, раствори-
602
мость в специфической среде вводимых веществ не определяется их растворимостью в воде.
Во время нахождения р/н в ЖКТ происходит облучение стенок пищеварительного тракта частицами, испускаемых радиоактивными изотопами.
3.4.Поступление р/н через кожные покровы
Впервом приближении поступление РВ через кожу существенно не отличается от других путей поступления. Относительно кожи термин «поглощение» определяет способность кожи впитывать в себя и удерживать вещества, находящиеся на её поверхности. Различают поврежденную и неповрежденную кожу, что обусловливает существенное различие в коэффициентах всасывания РВ. Большую роль относительно поглощенных энергии в коже играет обла-
дающий высокой радиочувствительностью слой эпидермиса (на глубине ~ 7 мг/см2), нарушение функций которого приводит к негативным изменениям процессов регенерации кожных покровов.
Р\н, поступающие в организм через кожу, создают опасность облучения как самой кожи, так и тех внутренних органов, в которые они будут доставлены кровотоком.
4.Тканевая доза, обусловленная излучением инкорпорированных радионуклидов
Вобщем случае доза, накопленная в некотором органе за время t от излучения РВ, поступивших в него в момент времени t = 0, определяется следующим соотношением:
t |
Eэфф (t) R(t) |
|
|
|
Dt = A0 k f1 (t) f2 (t) |
dt , |
(17.2) |
||
|
||||
0 |
m(t) |
|
||
где A0 – количество изотопа (активность), однократно поступив-
шего в организм нуклида;
f1 (t) – коэффициент всасывания радионуклида в кровь (из органов
дыхания, ЖКТ, кожи);
f 2 (t) – доля перехода РВ из крови в орган; 603
Eэфф (t ) – эффективная энергия, поглощаемая в органе на один
распад нуклида (с учетом ОБЭ);
R(t) – временная функция уменьшения активности за счет биоло-
гического вывода и радиоактивного распада нуклида; m(t) – масса органа;
к – размерный коэффициент.
Расчет тканевой дозы оказывается достаточно сложным в основном ввиду недостаточной информации относительно биологических процессов, а не физических параметров.
Входящая в соотношение (17.2) величина E эфф определяется
типом i-частиц излучения: |
|
Eэфф = E0,i (ООЭ) n , МэВ/расп.; |
(17.3) |
i |
|
где параметр n – фактор относительного повреждения; величина Е0,i определяет поглощенную в органе энергию излучения.
Для α-частиц, практически полностью поглощаемых в органе ввиду малых пробегов, оценка поглощенной энергии определяется соотношением:
E0,α = Eα φα , |
(17.4) |
где φα– доля распадов нуклида с испусканием α–частиц.
Для нуклидов, распадающихся с испусканием β–-частиц (электронов) в приближении их полного поглощения:
E |
− |
= 0, 33Emax φ |
β |
− (1 − |
Z1/ 2 |
) (1 + |
Emax |
) , |
(17.5) |
|
50 |
4 |
|||||||||
0,β |
|
|
|
|
|
|
где Z – атомный номер ядра-излучателя, φβ- – доля распадов нуклида с испусканием β-частиц.
В случае позитронных излучателей аналогичное соотношение имеет вид:
E0,β+ = 0,33Emaxφβ+ (1+ |
Emax |
) + 2φβ+ 0,511(1− e |
−μtr r* |
) , (17.6) |
4 |
|
где второе слагаемое учитывает вклад двух аннигиляционных фотонов с энергией 0,511 МэВ; μtr – коэффициент передачи энергии в
604
биологической ткани для аннигиляционных фотонов; r* – эффективный линейный размероргана (определяется далее).
Оценка поглощенной энергии для фотонов может быть сделана по соотношению:
−μtr (Eγ) |
r* |
(17.7) |
E0,γ = φγ Eγ (1− e |
) , |
где φγ – доля распадов нуклида с испусканием γ–квантов. Величина
AF =1− e |
−μ |
(E |
r*) |
(17.8) |
tr |
γ |
|
определяет эффективность взаимодействия фотонов в пределах объёма, содержащего равномерно распределенный γ-нуклид (фактор поглощения). Значение эффективного линейного размера органа r* в соответствии с его конфигурацией рассчитывается по соотношению:
r* |
2π π |
= 1 / 4π r(θ, φ) sin θdθd φ. (17.9) |
0 0
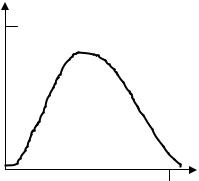
Поглощенная доза в водной сфере радиусом 5 см в зависимости от энергии γ-квантов для равномерно распределенных точечных изотропных источников представлена на рис. 17.5.
1
Доза, отн. ед.
0 0 |
1 Еγ, МэВ |
Рис. 17.5. Зависимость дозы от энергии источника гаммаквантов в сфере из воды;
Rсф.= 5см
605

5. Роль времени в формировании дозы излучения инкорпорированных нуклидов
Величина дозы в любом органе возрастает с течением времени нахождения в нем РВ. В соотношении (17.2) практически все параметры являются функциями времени. Прежде всего, за время пребывания в органе изменяется активность инкорпорированного изотопа (радиоактивный распад ~ exp(-λрt), где λр – постоянная распада) и параметры биологического выведения. Одновременно идет процесс биологического выведения нуклида, скорость которого зависит от соответствующей постоянной выведения λб. Результирующая скорость эффективного уменьшения активности нуклида определяется величиной
λэфф = λр + λб (17.10)
или периодом эффективного периода полувыведения:
T эфф = |
T р |
T б |
|
|
1/ 2 |
1/ 2 |
. |
(17.11) |
|
T р |
|
|||
1/ 2 |
+ T б |
|
||
|
1/ 2 |
1/ 2 |
|
|
Биологический период полувыведения определяется экспериментально. В качестве примера в табл. 17.3 приведены данные для двух изотопов и некоторых органов человека.
Таблица 17.3
Периоды полувыведения изотопов 137Cs и 90Sr из некоторых органов человека, (сутки)
137Cs |
|
|
90Sr |
||
Тело |
|
40 |
Тело |
|
5700 |
Легкие |
|
138 |
|
|
|
Кости |
|
138 |
Кости |
|
6400 |
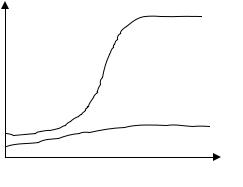
Период полувыведения зависит от возраста человека, что иллюстрируется на рис. 17.6 для изотопов 137Cs и 40К.
606
Если T1эфф/ 2 < 1 года, то можно пренебречь зависимостью функции W (массы) от времени, а так же других функций ( f1 (t), f 2 (t) , Eэфф(t) ) и принять A0 = 1, то
|
|
|
|
|
|
|
D(t) = C t R(t)dt , |
(17.12) |
|
|
|
|
|
|
|
|
|
0 |
|
где |
C = |
k f1 f2 |
Eэфф |
; функция |
R(t) определяет характер выве- |
||||
W |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
дения нуклидов. |
|
|
|
|
|
|
|
||
|
|
|
1 |
|
|
|
|
137Cs |
|
|
|
сутки |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
40K |
|
|
|
|
|
|
|
год |
5 |
||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
Рис. 17.6. Зависимость периода полувыведения нуклидов 137Cs и 40K от времени
6. Камерные модели
6.1. Общее рассмотрение
Попавшие в организм РВ вовлекаются естественными физиологическими процессами в перемещение между органами и тканями. Формирование дозы в каждом участке организма определяется накоплением и исчезновением РВ. Математическое описание движения инкорпорированных р/н внутри организма называют кинетикой радиотрассеров. Биологическая система представляется здесь как комбинация камер (или депо), связанных кинетическими процессами обмена вещества между камерами. Камерная модель состоит из конечного числа депо, каждое из которых ведет себя как отдельный гомогенный компонент целой биологической системы. Камера может представляться либо отдельным физическим про-
607
странством, таким как плазма крови или ткань мозга, либо разными химическими формами вещества, либо различными фармакологическими состояниями (связанное против несвязанного) радиотрассера, находящимися в одном и том же физическом пространстве. Количество или накопление материала в камерах может быть описано системой дифференциальных уравнений первого порядка.
Дифференциальное уравнение для i-й камеры, входящей в определенную систему организма, можно записать в следующем виде:
dq |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
i |
= −λp q |
− k |
i0 |
q |
+ |
|
(k |
ji |
q |
j |
− k |
ij |
q ) , (17.13) |
|
dt |
||||||||||||||
i |
|
i |
|
j=1 |
|
|
|
i |
где qi – активность р/н в i-камере; λp qi – скорость уменьшения
активности из-за распада нуклида;
ki0 qi – скорость уменьшения активности за счет процесса фиксации или выведения;
n
k ji q j – вклад других систем в i-ю систему;
j=1
n
kij qi – передача активности другим системам;
j=1
k ji , kij – константы переноса из одной систему в другую.
Таким образом, имеется система из n обыкновенных дифференциальных уравнений первого порядка. Задача нахождения концентраций нуклида может быть представлена в матричном виде:
|
|
d |
|
M = K M , |
(17.14) |
|
|
|
dt |
||||
|
|
|
|
|
||
где М – вектор-столбец концентраций активностей; |
|
|||||
|
k11 k12 − − − k1n |
|
|
|
||
|
|
|
|
|||
K = |
− − − − − − − − − |
|
– транспортная матрица. |
|
||
|
− − − − − − − − − |
|
|
|
||
|
kn1 kn2 − − − knn |
|
|
|||
608
6.2. Простая кинематика нуклидов в рамках однокамерной модели
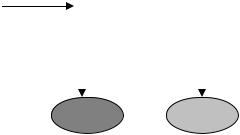
Рассмотрим какую-либо систему организма человека, например, циркулирующая кровь; р/н выводятся из этой системы или фиксируются в других органах и тканях. Соответствующая система обыкновенных дифференциальных уравнений, описывающая кинематику процессов перехода р/н (схема миграции нуклида показана на рис. 17.7):
dq1 |
|
= −(k1 + λp ) q1; |
|
|
|||
dt |
|
|
|
||||
dq f |
|
|
= a f |
k1 q1 − λp q1; |
(17.15) |
||
dt |
|
|
|||||
dqe |
|
= a k q − λ |
p |
q ; |
|
||
dt |
|
|
|||||
|
|
e |
1 1 |
e |
|
||
q0 = q1 (0) .
Входящие в уравнения переменные и константы имеют следующее значения:
q0 - начальная активность р/н в момент времени t = 0, входящего в
систему, Бк;
q1 (t) – текущее значение активности, Бк; m1 – масса системы или органа, кг;
k1 – коэффициент, определяющий скорость выведения нуклида из системы, с-1;
λp – постоянная распада нуклида, с-1;
a f , ae – коэффициенты, определяющие вывод нуклида в депо фиксации и резервуар выведения; a f + ae = 1 .
Параметр c1 = q1 / m1 , Бк/г – средняя концентрация активности в
рассматриваемой системе.
Решение системы (17.15) имеет вид: c1 (t) = c0 exp(−( λp + k1 ))·t;
c f (t) = c0 |
m1 |
a f exp(− λp ·t)·[1-exp(-k1·t)]; |
(17.16) |
|
|||
|
m f |
|
|
|
609 |
|
|
qe (t) = q0 ae exp(−λp t) [1 − exp(−k1 t)].
q0, |
|
|
|
|
|
|
|
q1, m1, c1, k1 |
|
|
|
|
|
t = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
a |
|
|
q |
|
|
|
|
|
qf, mf, cf |
|
|
|
|
|
||
выведение фиксация
Рис. 17.7. Блок - схема однокамерной модели.
Первые два уравнения (17.16) определяют концентрации активностей в системе и в депо фиксации; третье уравнение – активность выводимого нуклида.
Однокамерная модель часто является основной для расчета предельно допустимых поступлений радиоактивных нуклидов в организм человека. Ниже рассматривается пример оценки предельно допустимой концентрации радиоактивного 131I на основании установленной величины предельно допустимой годовой дозы в щитовидной железе, являющейся преимущественным депо фиксации йода (рассматривается случай ингаляционного поступления нуклида). Рассматривается упрощенное уравнение баланса скоростей поступления и вывода нуклида из органа:
dq |
= −λэфф q(t) + I0 f , |
(17.17) |
dt |
где q(t) – величина активности в органе в момент времени t; I0 - скорость поступления нуклида, Бк/с; λэфф – постоянная вывода
нуклида, 1/c; f – часть количества нуклида, поступившая в орган. Решение обыкновенного дифференциального уравнения (17.17):
610
