Кинематическая модель сферы (эллипсоида)

Модель представлена системой уравнений

x = (a²z²)  sin (80z),

y = (b²z²)  cos (80z),

z = N, …, N.

где a и b – размеры эллипсоида по осям x и y соответственно, N – некоторое численное значение по оси z, которым ограничивается эллипсоид. Задавая значения N можно формировать как полную, так и часть поверхности. При равенстве a и b будет сфера, при неравных значениях будет эллипсоид.

Поверхность образуется пространственной линией при движении по оси z с определенным шагом. На рис.1.34 намеренно взят большой шаг для того, чтобы показать механизм построения.

На рис.1.35 слева показана сфера, в которой множитель перед z равен 160; справа изображена та же фигура, но она значительно уплотнилась за счет того, что вышеупомянутый множитель приравнен 4000.

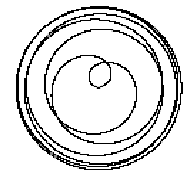
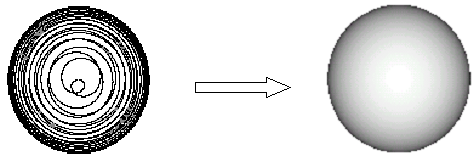
Рис. 1.34 Рис. 1.35

Кинематическая модель однополостного гиперболоида

Модель представлена системой уравнений

x = (a ²+z²)  sin (80z),

y = (b ²+z²)  cos (80z),

z = N, …, N.

где a и b – размеры горловины гиперболоида по осям x и y соответственно, N – некоторое значение по оси z которым ограничивается фигура. При равенстве a и b будет круговой гиперболоид, при неравных значениях будет эллиптический гиперболоид.

Здесь N определяет длину гиперболоида, в отличие от случая со сферой, так как он представляет бесконечную форму. И ограничение по z влияет не только на размер рассчитываемого пространства, но и на вид получаемой фигуры. Для лучшей наглядности выполним поворот поверхности в пространстве вокруг всех трех осей системы координат на 30 градусов (рис.1.36).

У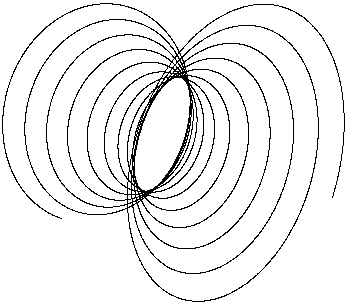меньшив шаг построения, получаем гиперболоид на рис.1.37.

Рис. 1.36 Рис.1.37

Кинематическая модель двуполостного гиперболоида

Модель представлена системой уравнений

x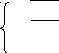 = (-a ²+z²)  sin (80z),

y = (-b ²+z²)  cos (80z),

z = N, …, N.

где a и b – размеры «чаш» гиперболоида по осям x и y соответственно, N – некоторое значение по оси z, которым ограничивается гиперболоид. При равенстве a и b будет круговой гиперболоид, при неравных значениях будет эллиптический гиперболоид.

С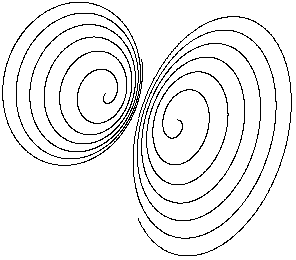 большим шагом построения двуполостный гиперболоид показан на рис.1.38. С малым шагом построения двуполостный гиперболоид показан на рис.1.39.

Рис. 1.38 Рис.1.39

Кинематическая модель конуса второго порядка

Модель представлена системой уравнений

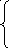x = а  z  sin(z)

y = b  z  cos(z) ,

z = -N … N

где N – некоторое значение по оси z, которым ограничивается конус. При равенстве a и b будет круговой конус, при неравных значениях будет эллиптический конус.

С большим шагом построения конус показан на рис.1.40. С малым шагом построения конус показан на рис.1.41.

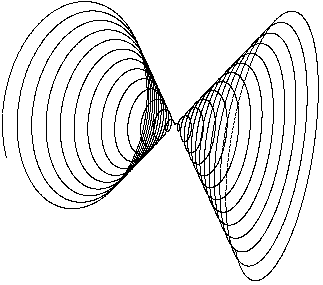
Рис. 1.40 Рис. 1.41