4. Анализ электропривода с двухзонным регулированием как объекта управления.

1. Определение состава выходных координат ОУ. В качестве выходных координат мы можем получить: угловую частоту вращения w, ток якоря I, угол поворота вала двигателя φ, момент сопротивления М и т д;

2. Выбор выходной координаты. По заданию нам необходимо регулировать скорость.

3. Определение управляющих координат. Управление электроприводом можно вести с помощью следующих управляющих координат: напряжение якоря U_Я, напряжение обмотки возбуждения U_В, сопротивление якоря R_Я и т д.

4. Выделим из состава управляющих координат ту которой будем управлять. Согласно заданию управляющими координатами должны быть: напряжение якоря U_Я, напряжение обмотки возбуждения U_В.

5. Определение возмущающих воздействий. По заданию возмущающими воздействиями являются:

- изменение момента сопротивления ∆ М_с;

- изменение момента инерции ∆J;

-изменение сопротивления резисторов ∆R вследствие изменения температурного режима;

- изменение магнитной проницаемости железа ∆μ;

- отклонение напряжения промышленной сети ∆U_С.

6. Определение диапазона изменения каждого возмущения.

Диапазон изменения каждого возмущения:

- изменение момента сопротивления по заданию ∆ М_с=Мн…М_хх

- изменение момента инерции по заданию ∆J=J_н…2*J_н;

-изменение сопротивления резисторов по заданию ∆R вследствие изменения температурного режима ∆R=R_н-1.25…R_н;

- изменение коэффициента передачивследствие изменения магнитной проницаемости железа ∆μ по кривой намагничивания (определяется ниже)= 0.0918…0.17;

- отклонение напряжения промышленной сети по заданию ∆U_С=+10%...-15% от номинального значения.

7. Проверка необходимости создания системы автоматического регулирования (САР).

Проверим изменение скорости двигателя при изменении момента сопротивления ∆ М_с по механической характеристики.

Ток короткого замыкания определим по формуле:

А

Уравнение электромеханической характеристики имеет вид:

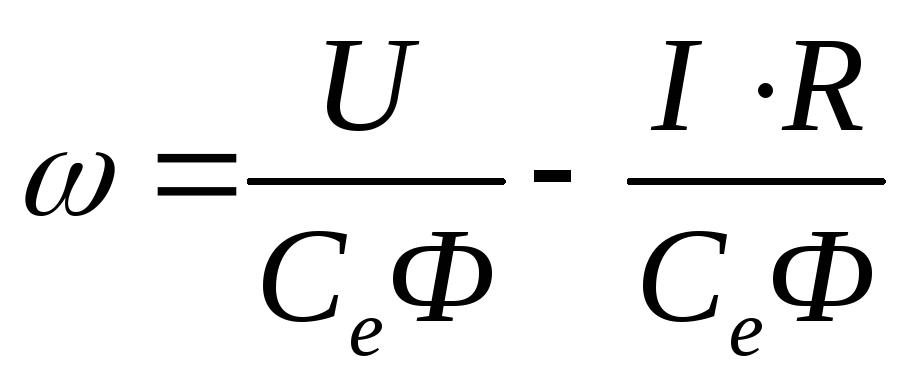
Подставляя значения Iкз, Iн, ω_н находим значение скорости идеального холостого хода

рад/с

Таким образом при изменении момента сопротивления ∆М_с=Мн…М_хх скорость двигателя изменяется: ∆w=274…209.33 рад/с.

По заданию скорость двигателя должна отклонятся не более 0.1%. По расчёту скорость двигателя при изменении момента сопротивления отклоняется на 30%. При совместном действии всех возмущений скорость двигателя может изменяться в ещё больших пределах. Для обеспечения заданной точности поддержания скорости необходима разработка САР.

5. Разработка математической модели электропривода.

5.1. Определение передаточной функции цепи якоря.

Схема замещения якорной цепи двигателя постоянного тока изображена на рисунке:

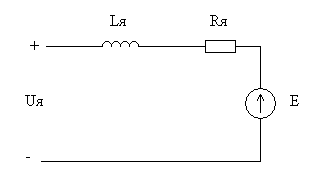
Уравнение электрического равновесия для этой схемы имеет вид:

Запишем уравнение равновесия моментов для вращательного движения (уравнение движения привода):

Запишем уравнение, связывающее ЭДС вращения двигателя Е и угловую скорость двигателя ω:

Момент, развиваемый двигателем, связан с током якоря и магнитным потоком следующей зависимостью:

Таким образом, можно составить систему уравнений, описывающую электрическую и механическую части якоря электродвигателя постоянного тока:

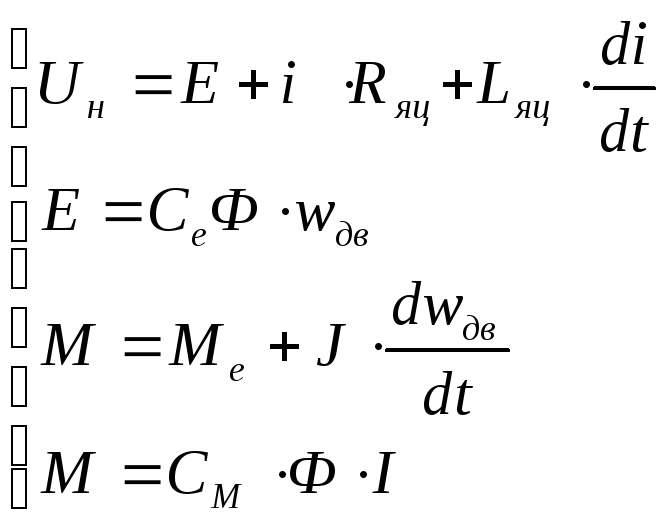
С учётом выше записанной системы уравнений составим структурную схему якоря двигателя постоянного тока при управлении изменением напряжения якоря:

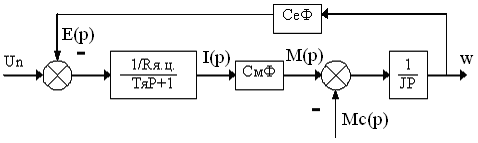
Рис 1. Схема электродвигателя.

Постоянную времени якорной цепи Тя определяют по следующей формуле:

,

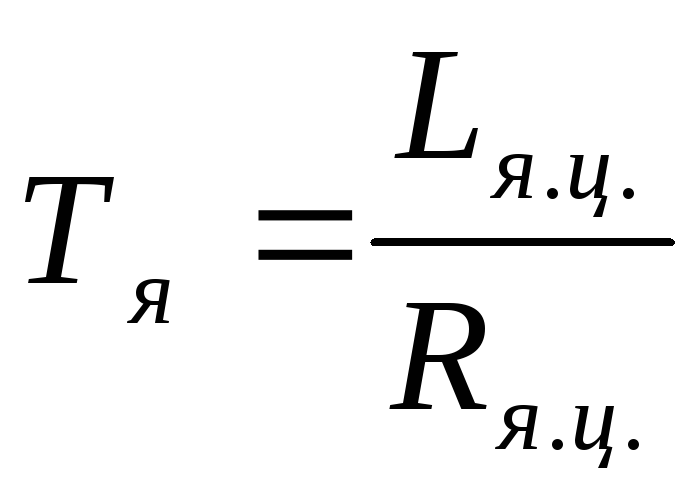где Lя.ц – индуктивность якорной цепи;

Rя.ц – сопротивление якорной цепи.

Индуктивность якорной цепи вычисляют по формуле:

,

где Lтр – приведенная индуктивность трансформатора:

Lя.д.- индуктивность якоря двигателя

Приведенную индуктивность обмотки трансформатора определяют по формуле:

,

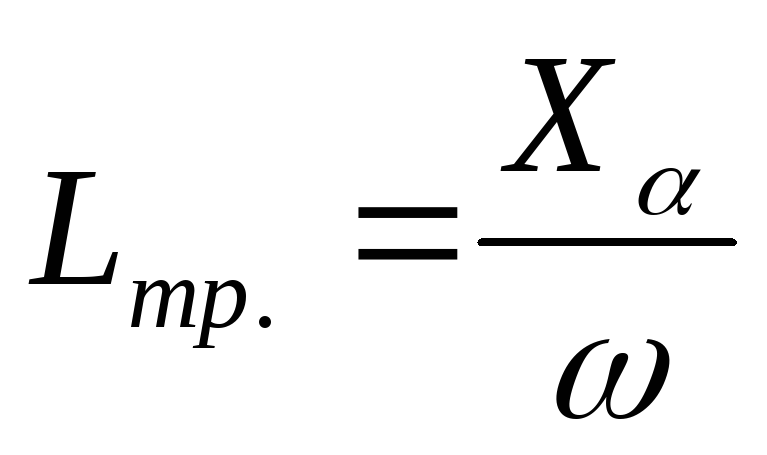где Xα – приведённое индуктивное сопротивление обмоток трансформатора;

ω – угловая частота питающей сети.

,

где Zтр – полное приведенное сопротивление обмоток трансформатора;

Rтр – приведенное активное сопротивление трансформатора.

Полное приведенное сопротивление обмоток трансформатора вычисляют по формуле:

,

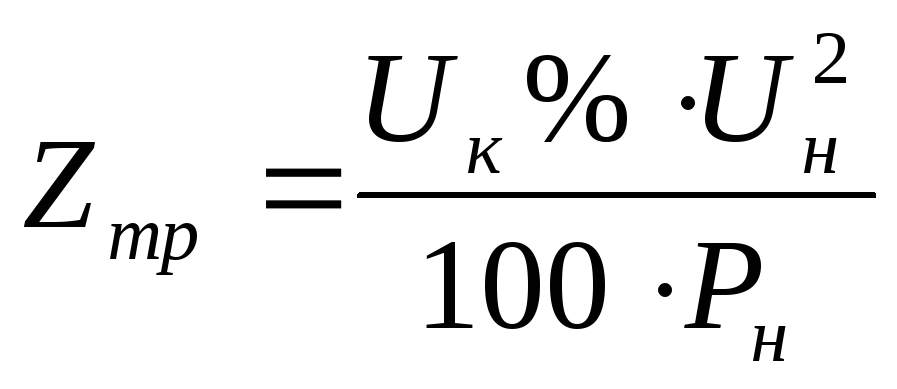где Uк – напряжение короткого замыкания;

Pн – номинальная мощность трансформатора;

Uн – номинальное напряжение вторичной обмотки.

Подставив численные значения, получим:

Ом

Приведенное активное сопротивление трансформатора определяют по формуле:

,

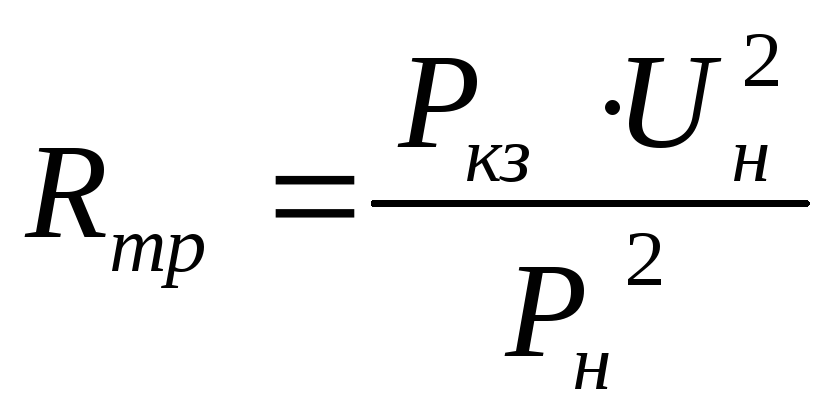
где Pк.з.- потери при коротком замыкании.

Подставив значения в данную формулу, получим следующее значение:

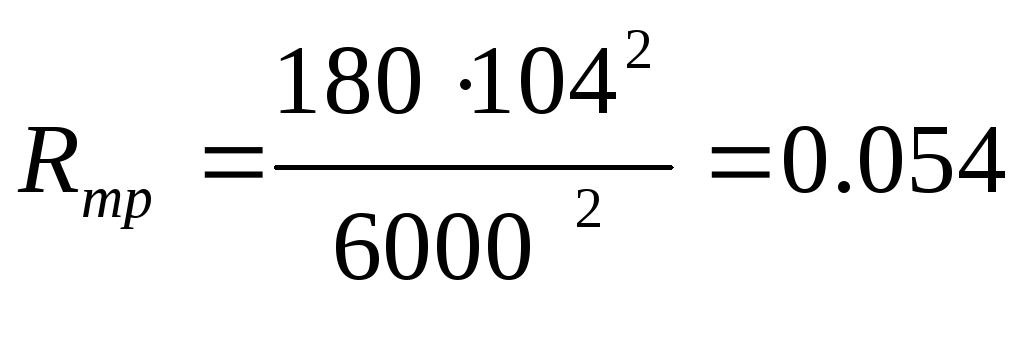Ом

Подставив полученные значения в формулу, получим значение приведенного сопротивления обмоток трансформатора

Подставив полученные значения в формулу, получим значение приведенной индуктивности обмотки трансформатора

Гн

Индуктивность якоря двигателя определяют по формуле:

Гн,

Подставив полученные значения в формулу, получим значение индуктивности якорной цепи:

Гн

Полное сопротивление якорной цепи вычисляют по формуле:

Сопротивление якоря двигателя:

,

где Rя – сопротивление якорной обмотки;

Rд.п – сопротивление дополнительной обмотки;

Rк.о. – сопротивление компенсационной обмотки;

Rщ – сопротивление щеточного контакта.

Сопротивление щеточного контакта определяют по формуле:

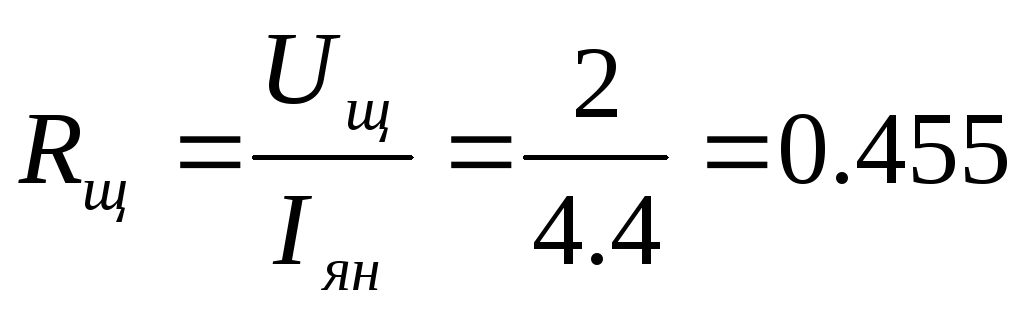Ом,

Подставив значения в формулу, получим значение сопротивления якоря двигателя:

Ом

Динамическое сопротивление тиристора вычисляют по формуле:

,

где Uт=13 В – классифицикационное падение напряжения на тиристоре;

Iт.н – среднее значение тока через тиристор при номинальном моменте сопротивления на двигателе.

Среднее значение тока через тиристор определяется по формуле:

А

Подставив полученное значение в формулу получим:

Ом

Коммутационное сопротивление тиристора определяют по формуле

,

где m- число фаз преобразователя

Ом

Подставив полученные значения в формулы, получим следующие результаты:

с.

Момент инерции двигателя определим из выражения:

кг*м^2

Конструктивный коэффициент машины по ЭДС определим по формуле

В*с/рад

Конструктивный коэффициент машины по моменту определим по формуле:

Н*м/А