Введение

Настоящие пособие включает в себя комплекс лабораторных работ по курсу “Теория автоматического управления “, который входит в учебный план подготовки инженеров по специальностям 220201.65 – «Управление и информатика в технических системах» и 220301.65 – «Автоматизация технологических процессов и производств (полиграфия)» и направлению 220200.62 – «Автоматизация и управление».

Лабораторные работы выполняются в третьем и пятом семестрах. Цель этих работ – исследование временных и частотных характеристик типовых звеньев, изучение их особенностей.

Правила подготовки и проведения лабораторных работ

Студенты проходят инструктаж по технике безопасности в лабораториях кафедры автоматизации полиграфического производства.

При подготовке к работе студент обязан дома изучить связанные с ней вопросы теории и знать порядок выполнения работы. При этом он должен оформить теоретическую часть ответа в виде конспекта раздела 2.

Перед началом работы студент должен предъявить преподавателю оформленную теоретическую часть лабораторной работы.

После выполнения экспериментальной части работы с применением программных средств символьной математики Mathcad студент должен предъявить результаты расчетов преподавателю, учебному мастеру или лаборанту.

В соответствии с заданием студент выполняет дома расчетно-графическую часть работы, которая должна содержать:

• обработку результатов работы в виде графиков, выполненных на миллиметровой бумаге в требуемом масштабе;

• расчет необходимых параметров;

• сопоставляем и оцениваем экспериментальных и теоретических данных.

Отчет по лабораторной работе должен быть построен по следующему плану:

• назначение и ее цель;

• теоретическая часть;

• экспериментальная часть (краткое описание хода выполнения лабораторной работы и протоколы результатов расчетов с применением программных средств символьной математики Mathcad);

• расчетно-графическая часть;

• выводы о результатах выполнения работы.

Отчет оформляется к началу очередного занятия. После этого он должен быть защищен студентом и подписан преподавателем.

Работа № 1

Решение линейных дифференциальных уравнений в математической системе Mathcad

Продолжительность работы – 4 часа

1. Цель работы

Ознакомление с математической системой Mathcad. Получение навыков работы и решения уравнений с применением программных средств символьной математики Mathcad.

2. Теоретическое обоснование

Функционирование системы управления и любого ее элемента (звена) может быть описано дифференциальным уравнением, в общем случае нелинейным. Если x - входная, y - выходная координата, а z - внешнее возмущение, то уравнение работы системы имеет вид:

F(y,, ... x, ,...) + z = 0 (2.1)

Это выражение называется уравнением динамики системы.

В установившемся режиме работы x = x _уст = const, y = y _уст = const, поэтому все производные будут равны нулю и уравнение (2.1) примет вид:

F ( y_уст , 0, 0 ... x _уст , 0, 0 ...) + z _уст = 0 (2.2)

Полученное уравнение носит наименование уравнения статики системы. Зависимость y _уст = f (x _уст) называется статической характеристикой системы.

В случае, когда система имеет k входов и l выходов, ее функционирование описывается системой l уравнений:

F₁ (y₁ ,₁,₁ ... x₁, ₁,₁... x_k , _k ,_k ...) + z = 0 (2.3)

F₂ (y₂ ,₂ ,₂ ... x₁, ₁,₁... x_k, _k,_k...) + z = 0 (2.4)

F_l (y_l ,_l ,_l ... x₁, ₁,₁... x_k, _k,_k...) + z = 0 (2.5)

Им соответствует и l уравнений статики:

F₁ ( y _1уст , 0, 0 ... x _1уст , 0, 0 ... x _kуст , 0, 0 ...) + z _уст = 0 (2.6)

F₂ ( y _2уст , 0, 0 ... x _1уст , 0, 0 ... x _kуст , 0, 0 ...) + z _уст = 0 2.7)

F_l ( y _lуст , 0, 0 ... x _1уст , 0, 0 ... x _kуст , 0, 0 ...) + z _уст = 0 (2.8)

Во многих случаях при анализе систем управления нелинейные дифференциальные уравнения можно заменить линейными, которые приближенно описывают функционирование системы.

Если отклонение координат системы от расчетного режима ∆y = y – y₀, ∆x = x – x₀ малы, то линеаризация может быть осуществлена путем разложения функции F(y,,... x,,...) в ряд Тейлора в окрестности координат y₀ ,₀ ,₀ ... x₀ , ₀ ,₀ ... . Это разложение возможно, если нелинейная функция непрерывна и дифференцируема по всем координатам.

О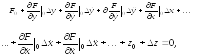 тбрасывая в разложении ряд слагаемых высшего порядка малости, получаем:

Где введены обозначения

F₀ = F( y₀ ,₀ ,₀ ... x₀, ₀,₀..). (2.10)

, =₀ , =₀ ,…, x= x₀ ,= ₀ , = ₀ (2.11)

Вычитая из уравнения (2.9) очевидное уравнение

F₀+ z₀=0 (2.12)

Получаем

a_n ∆ y⁽ⁿ⁾+ a_n-1∆y^(n-1)+...+ a₁ ∆y’+ a₀ ∆y=b_m ∆x^(m)+ a_m-1 ∆x^(m-1)+...+ b₁ ∆x’+ b₀ ∆ (2.13)

Где коэффициенты a_n и b_m равны

…

…

Рассмотрим пример нахождения уравнений работы элементов систем управления, построенных на различных физических принципах.

Например для центробежного измерителя скорости вращения уравнение перемещения ползуна имеет вид:

г де - центробежная сила;

Fпр = Fпр (у) - сила пружины;

Fтр = Fтр (у,ý) - сила сухого и жидкостного трения;

m – масса подвижных частей;

m_г - масса грузиков 2;

r – радиус вращения грузиков;

n – скорость вращения.

Е сли сухое трение отсутствует, то

где k₁ - коэффициент вязкого трения.

Сила пружины может быть принята в виде

F_пр(y)= k_2y (2.16)

Следовательно, уравнение перемещения ползуна будет:

Ц ентробежная сила здесь зависит не только от скорости вращения n, но и от координаты y, так как она связана с радиусом вращения грузиков r.

Линeйныe диффepeнциaльныe ypaвнeния (ЛДУ) мoжнo paздeлить нa двe гpyппы: ЛДУ c пocтoянными кoэффициeнтaми и ЛДУ c пepeмeнными кoэффициeнтaми. К пocлeдним oтнocятcя тe ypaвнeния, в кoтopыx xoтя бы oдин из кoэффициeнтoв являeтcя фyнкциeй кaкoгo-либo apгyмeнтa. B дaннoм пocoбии тaким apгyмeнтoм являeтcя вpeмя t .

По форме задания и те, и другие ЛДУ могут иметь вид одного уравнения порядка n или вид системы из n уравнений первого порядка (форма Коши). переход от одной формы к другой будет показан ниже.