2.1.5. Преобразование логических выражений
Табличный способ определения истинности сложного выражения имеет ограниченное применение, так как при увеличении числа логических переменных приходится перебирать слишком много вариантов. В таких случаях используют способ приведения формул к нормальной форме. Формула имеет нормальную форму, если в ней отсутствуют знаки эквивалентности, импликации, двойного отрицания, при этом знаки отрицания находятся только при переменных.
Основные формулы преобразования логических выражений:
1. ¬ ¬ A ≡ A
2. ¬ (А & В) ≡ ¬ А
¬ В.
3. ¬ (А
В) ≡ ¬ А & ¬ В.
4. ¬ (А → В) ≡А & ¬ В.
5. А→B ≡ ¬ A
B.
6. А ↔ В ≡ (А & В)
(¬ А & ¬ В) ≡ (¬ А
В) & (А
¬ B).
7. А & (А
B)
≡ А.
8. А
А & В ≡ А.
9. ¬ А & (А
В) ≡ ¬ А & В.
10. A
¬ А & В ≡ А
В.
11. Законы коммутативности:
А & В ≡ В & А;
А
В ≡ В
А.
12. Законы ассоциативности:
(A
B)
С ≡ А
(В
С);
(А & В) & С ≡ А & (В & С).
13. Законы идемпотентности:
А
А ≡ А;
А & А ≡ А.
14. Законы дистрибутивности:
А & (В
С) ≡ (А & В)
(А & С);
А
(В & С) ≡ (А
В) & (А
С).
15. А
1 ≡ 1;
16. А & 1 ≡ А;
17. ¬ А
А ≡ 1;
18. А & 0 ≡ 0;
19. А & ¬ А ≡ 0.
Пример 9. Упростить следующую логическую формулу (в фигурных скобках указан номер использованной формулы преобразования):
.
Решение.
= {4}
(A
B)
&
= {1}
(A
B)
& (B
C)
=
{14}
(A
B)
& B
(A
B)
& C = {11
и
14}
A & B
B
A
& C
B
& C =
{14,
15 и
16}
B & (A
1)
C
& (A
B)
= B
A
& C
B
& C =
{11
и
12}
B (1
C)
A
& C = {15}
B
A
& C
Индивидуальные задания
Задания распределяются в зависимости от выданного преподавателем mn-кода. Если m — число нечетное, то ваш вариант 1, если четное — вариант 2.
Задание 1. Используя логические операции, запишите высказывания, которые являются истинными при выполнении следующих условий:
Вариант 1. 1) хотя бы одно из чисел X, Y, Z положительно;
2) только одно из чисел X, Y, Z не является положительным.
3) только одно из чисел X, Y, Z больше 10
4) ни одно из чисел X, Y, Z не равно 104
Вариант 2. 1) хотя бы одно из чисел X, Y, Z отрицательно;
2) только одно из чисел X, Y, Z является отрицательным.
3) только одно из чисел X, Y, Z не больше 10
4) каждое из чисел X, Y, Z равно 0
Задание 2. Определите значение логического выражения не (X>Z) и не (X=Y), если:
Вариант 1. 1) X=3, Y=5, Z=2;
2) X=5, Y=0, Z=–8.
Вариант 2. 1) X=9, Y=–9, Z=9;
2) X=0, Y=1, Z=19.
Задание 3. Пусть a, b, c — логические величины, которые имеют следующие значения: а = истина, b= ложь, c = истина. Нарисуйте логические схемы для следующих логических выражений и вычислите их значения:
Вариант 1. 1) а и b;
2) не а или b;
3) а или b и с;
4) (а или b) и (c или b).
Вариант 2. 1) а или b;
2) а и b или с;
3) не а или b и с;
4) не (а и b и с).
Задание 4. Построить логические схемы по логическому выражению:
Вариант 1. x1 и (не x2 или x3).
Вариант 2. x1 и x2 или не x1 и x3.
Задание 5. Выполните вычисления по логическим схемам. Запишите соответствующие логические выражения:
Вариант 1. Вариант 2.
Задание 6. Дана логическая схема. Построить логическое выражение, соответствующее этой схеме.
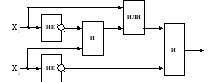
Вычислить значение выражения для:
Вариант 1. 1) x1=0, x2=1;
2) x1=1, x2=1.
Вариант 2. 1) x1=1, x2=0;
2) x1=0, x2=0.
Задание 7. Дана логическая схема. Построить таблицу истинности для данной схемы.
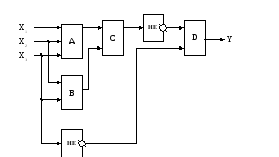
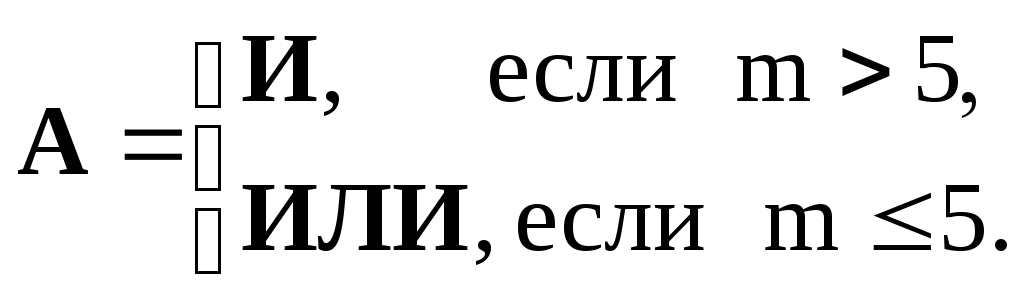
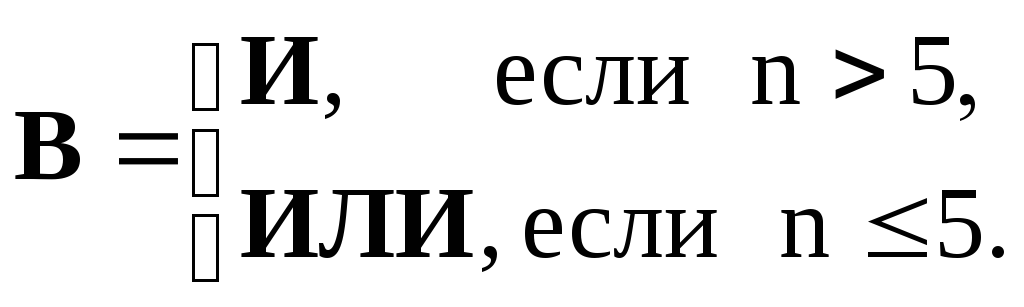
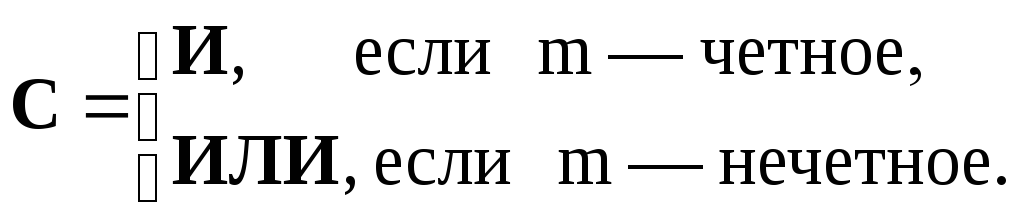
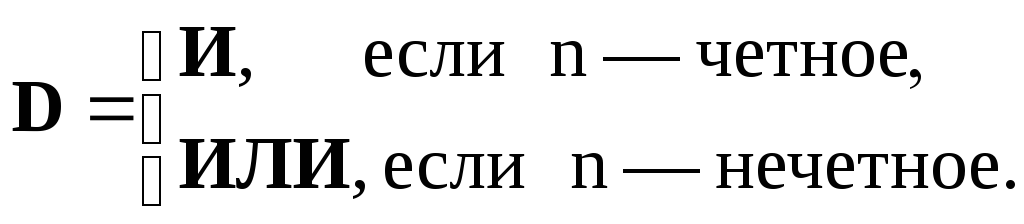
Задание 8. Определить истинность формулы:
Вариант 1. ((a
)
.
Вариант 2. 
.
Задание 9. Упростите выражение:
Вариант 1. 
.
Вариант 2. 
.
Подготовить отчет о проделанной работе.
В ОТЧЕТЕ ОБЯЗАТЕЛЬНО УКАЗАТЬ СВОЙ mn-КОД.