Содержание:

1. Выбор типоразмера двигателя и расчет редуктора

1.1) Предварительная оценка передаточного числа редуктора

1.2) Расчет редуктора с цилиндрическими колесами

1.3) Проверка пригодности двигателя с рассчитанным редуктором

2) Расчет усилителя мощности

3) Передаточная функция нестабилизированной разомкнутой системы

3.1) Функциональная схема разомкнутой нестабилизированной системы

3.2) Структурная схема и передаточная функция двигателя с учетом редуктора и нагрузки

3.3) Оценка общего коэффициента передачи разомкнутой системы

4) Коррекция следящей системы с использованием жесткой обратной связи

5) Определение параметров предварительного усилителя

5.1) Предварительный усилитель для СС с асинхронным двигателем

Исходные данные:

Таблица 1

Вариант	Наибольшая скорость вращения исп. вала, р/с	Амплитуда ускорения исп. вала , р/с2	Статический момент сухого трения на исп. валу Мнс ,	Момент инерции нагрузки на исп. валу ,	Максимально допустимое время перерегули-рования tp , c	Сумма стат. и кин. погрешно-стей при равномерной заводке , град	Дин. погрешность при синусной заводке , град
А12	2.71	13.2	1.25	26.9	0.1	1.0	2

1) Выбор типоразмера двигателя и расчет редуктора

Оценим требуемую мощность на валу двигателя по одному из следующих соотношений:

(1.1)

(1.2)

(1.3)

По формуле (1.2) получаем:

Тогда из условия выбираем двухфазный асинхронный двигатель серии ЭМ-8М.

Технические данные двухфазного асинхронного двигателя ЭМ-8М

Таблица 2

Uун, В	Рн, Вт	Мп,	, р/с	,	Ry , Ом	xy , Ом	D, мм	f, Гц
80	8.22	31.4	670	206	58.1	81.4	4	400

1.1) Предварительная оценка передаточного числа редуктора

Номинальные значения момента и скорости приближенно определяются из следующих соотношений:

Линеаризованная механическая характеристика двигателя для скоростей определяется по формуле:

, (1.4)

где (1.5)

Найдем коэффициент а по формуле (1.5) и подставим полученное значение в формулу (1.4):

(1.6)

Требуемый момент определяется по следующей формуле:

(1.7)

Подставляя значения в формулу (1.5) получаем:

(1.8)

Приравниваем правые части (1.6) и (1.8) и получаем квадратное уравнение для определения диапазона допустимых значений передаточных чисел редуктора:

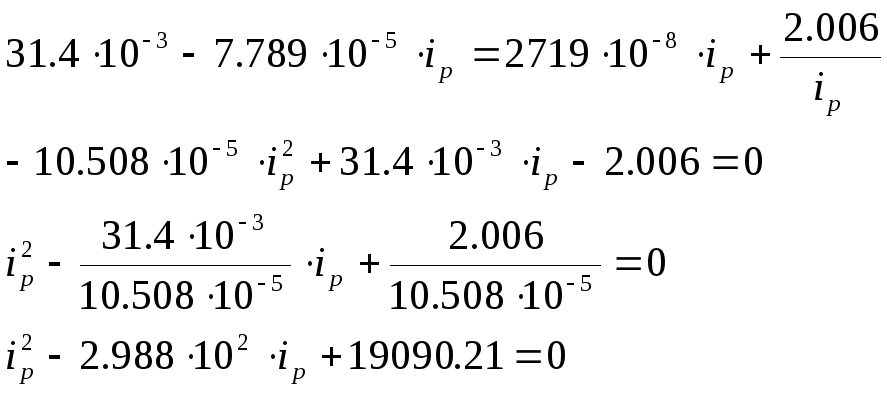
Получаем передаточные числа редуктора в диапазоне:

Исходя из двух корней квадратического уравнения выбираем передаточное чило редуктора ближе к 206.23, т. е. 150.

Выбранное передаточное число редуктора должно удовлетворять трем условиям, обеспечивающим нормальную работу двигателя:

• условие по скорости

(1.9)

• условие по моменту

, где (1.10)

• условие по перегреву

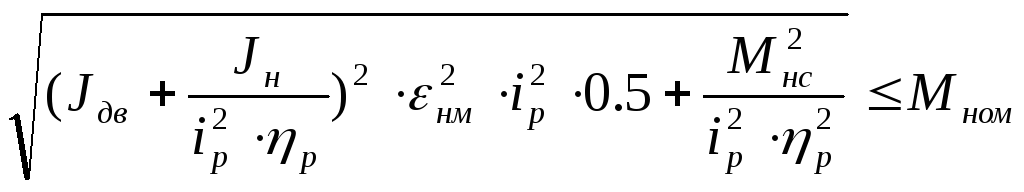
1.2) Расчет редуктора с цилиндрическими колесами

Выбранное передаточное число редуктора . Из условиязадаем передаточное число последней ступени. Пусть. Тогда рассчитаем передаточные числа каждой пары зацепления по формуле:

Проверка

Проверка

Получили 4 ступени и передаточное число первой ступени, не превышающее 2: 1<1.08<2

Из условия запишем:

Рассчитаем диаметр колес и количество зубьев шестеренок. Расчет диаметров колес ведется из условия, что диаметры всех ведущих шестерен одинаковы:

, гдеd– диаметр вала двигателя

Количество зубьев на ведущих шестернях должно быть:

Диаметр шестерни и количество зубьев на шестерне связаны соотношением:

, гдеm– модуль зуба(1.13)

В расчетном задании диаметр вала . Тогда получаем:

Диаметры ведомых шестерен рассчитывается по формуле:

(1.14)

Оценим величину модуля зуба:

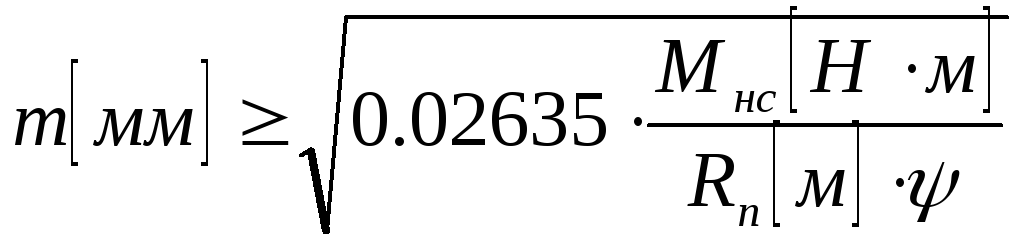, где- радиус последней шестерни (1.15)

Т.к. ширина шестерни , то. Возьмеми рассчитаем величину модуля зуба по формуле (1.14):

По ГОСТу выбираем . Тогда ширина шестерни

Проверим теперь выполнение условия обеспечения прочности зуба по формуле:

, (1.16)

где - динамический коэффициент

- коэффициент перекрытия

- коэффициент формы зуба

Причем для стальных колес должно выполняться условие:

Условие выполняется. Теперь уточним размеры колес редуктора. По формуле (1.15) пересчитаем радиус последней шестерни редуктора:

Тогда диаметр последней шестерни редуктора и соответственно передаточное число последней пары зацепления будут равны:

Пересчитаем остальные передаточные числа по формуле (1.12) и получим:

ПроверкаПроверка

Уточним передаточное число редуктора:

Теперь пересчитаем диаметры ведущих и ведомых шестерен и посчитаем количество зубьев на них по формуле (1.13):

Рассчитаем приведенный момент инерции к валу двигателя редуктора по формуле:

(1.17)

Для этого рассчитаем момент инерции каждого сплошного цилиндрического колеса по формуле:

, (1.18)

где - плотность материала, из которого изготавливаются колеса

Тогда по формуле (1.17) получаем приведенный момент инерции:

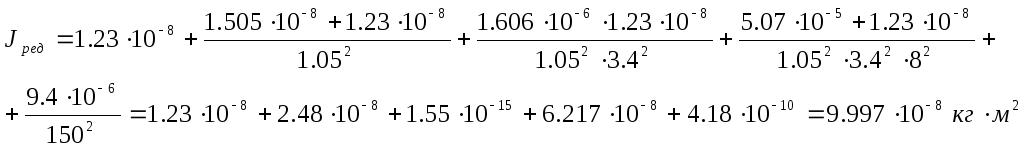
1.3) Проверка пригодности двигателя с рассчитанным редуктором

Проведем все три проверки с уточненным значением и полученной оценкой:

• по моменту

(1.18)

(

• по скорости

(1.19)

• по перегреву

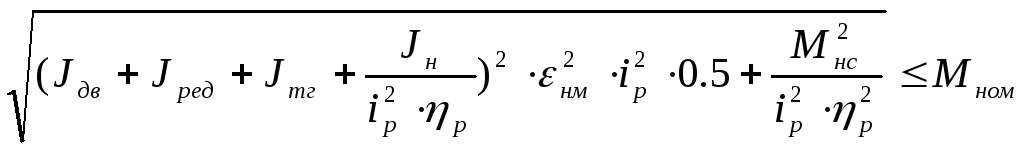(1.20)

Все неравенства выполняются. Выбранный двигатель с рассчитанным редуктором подходит для использования его в проектируемой системе.