Задача №2.

Приводятся сведения по регионам Европейской части России.

Регионы	Численность занятых в экономике		Среднеме-сячный душевой доход населения, руб.	Стоимость валового регионального продукта в среднем на
	Всего, млн. чел.	В % от численности населения		1-го занятого в экономике, тыс. руб.	1 руб. стоимости основных фондов в экономике, коп.
Волго-Вятский	3,59	43,2	860	27,2	14,5
Центрально-Чернозёмный	3,15	40,5	1059	27,9	12,5

Задание:

Выполните расчёт абсолютных и относительных показателей вариации, коэффициент асимметрии и показатель моды, постройте на одном графике гистограмму и полигон распределения частот, выпол­ните анализ полученных результатов.

Решение:

1. Найдем среднюю долю занятых по обоим регионам (в долях):

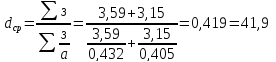
Форма - явная, вид - средняя гармоническая.

2.Найдем средний среднемесячный душевой доход по обоим регионам, используя формулу: Ч = 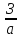– численность населения

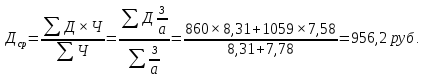Форма - явная, вид - средняя гармоническая.

3.Найдем среднюю производительность труда по обоим регионам

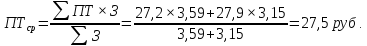
Форма -явная, вид - средняя гармоническая.

4. Средний показатель фондоотдачи рассчитать невозможно, т.к. нет данных о величине основных фондов по каждому региону.

Задача №3.

Приводятся данные за 2002 год о распределении территорий РФ по уровню среднемесячной начисленной заработной платы, тыс. руб.

Группы территорий РФ по уровню среднемесячной начисленной заработной платы, тыс. руб.	Число территорий в каждой группе
От 0,51 до 0,82	4
От 0,82 до 1,13	28
От 1,13 до 1,44	19
От 1,44 до 1,74	11
От 1,74 до 2,02	7
Итого:	69

Задание:

Выполните расчёт средних значений каждого показателя, ука­жите вид и форму использованных средних, приведите расчётные формулы. Проверьте правильность результатов.

Решение:

Найдем середины интервалов: 0,665; 0,975; 1,285; 1,59; 1,895 соответственно.

Перейдем от интервального ряда к моментному, заменяя каждый интервал его серединой Хш (числа в скобках в первом столбце таблицы). Найдем среднее значение признака:

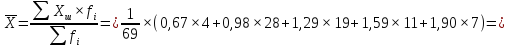
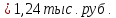
Найдем абсолютные показатели вариации:

1. Размах

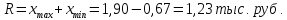
2. Среднее линейное отклонениe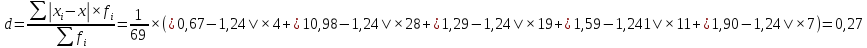

3. Среднее квадратичное отклонение

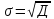
Дисперсия

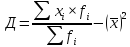
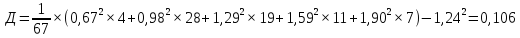
Среднее квадратичное отклонение

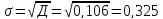
Найдем относительные показатели вариации:

1 . Средний относительный размах f =R/x = 1,23/1,24 = 0,922

2. Среднее линейное отклонение l = d/x = 0,275/1,24= 0,222

3. Коэф-т вариации V = σ/x100%=0,325/1,24100% = 26,2%

Найдем показатель моды:

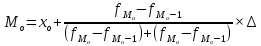
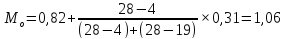
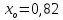нижняя граница модального интервала с наибольшей частотой.

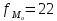частота модального интервала.

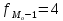частота в предыдущем интервале.

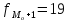частота в последующем интервале.

Д=1,3-0,82= 0,31 длина модального интервала.

Коэффициент ассиметрии Пирсона есть

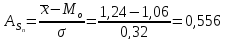
Коэффициент ассиметрии Пирсона больше единицы, т.е. ассиметрия правосторонняя.

Построим на одном графике гистограмму и полигон частот.

Гистограмма - ступенчатая фигура, каждый столбик которой имеет основной соответствующий интервал и по высоте равен её частоте.

Полигон строится следующим образом: из каждой точки 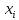восстанавливается перпендикуляр высотой 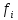, а затем верхние концы перпендикуляров соединяются последовательно ломаной линией.

Гистограмма

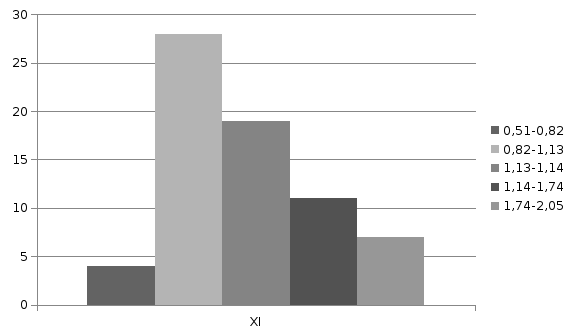
Полигон

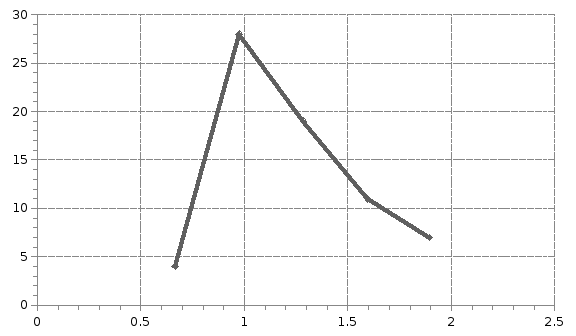
Выводы: 1.Коэффициент вариации V=26,2% > 20% следовательно, совокупность неоднородная.

2. 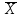= 1,24 и 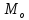= 1,06 принадлежат разным интервалам, следовательно, средняя V не является типичной для этой совокупности.

3. Коэффициент ассиметрин Пирсона 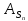больше единицы, т.е. ассиметрия правосторонняя.