4.2 Составление единого уравнения двигателя.
Из уравнения (11) выделяется Iи подставляется в уравнение (10), вследствие чего получаем:
В итоге получаем единое уравнение двигателя для двух инерционностей:
- электромагнитная постоянная времени.
4.3 Составление структурной схемы двигателя в двух вариантах.
Первый вариант структурной схемы:
Рис.9 Первый вариант структурной схемы
Положив момент сопротивления равным нулю:
Рис.10 Первый вариант структурной схемы двигателя в режиме холостого хода
Для данной структурной схемы возможно наблюдение за изменением скорости, но не за изменением тока.
Для возможности наблюдения за изменением тока и скорости одновременно необходимо в уравнениях (10) и (11) перейти к производной ЭДС двигателя по времени.
Так же как и в пункте 3.3 и получаем уравнение для составления второго варианта структурной схемы:
Рис.11 Второй вариант структурной схемы
Удалив обратную связь по ЭДС двигателя, получаем схему для исследования режима короткого замыкания:
Рис.12 Второй вариант структурной схемы в режиме короткого замыкания
4.4 Определение характера переходного процесса по постоянным двигателя.
- характеристический полином
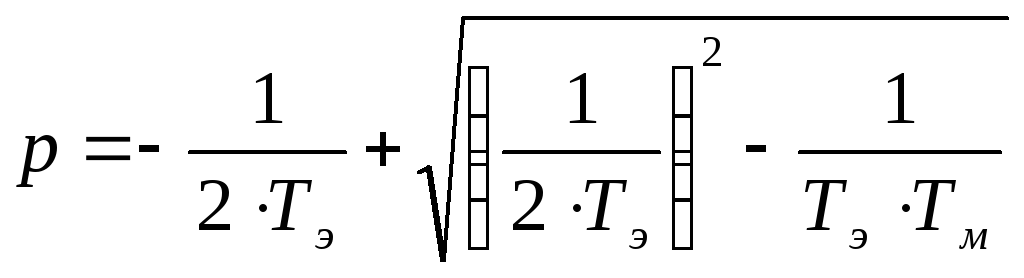
Т.к. отрицательный дискриминант говорит о наличии комплексных корней, что, в свою очередь, свидетельствует о наличии колебательных процессов, то:
- условие колебательности
По полученным расчетам Тэ= 0,1468 и Тм= 0,256
То есть 0,0,1468 > 0,064, переходной процесс будет колебательным.
5. Выполнение моделирования динамических процессов для пунктов 3 и 4, при номинальном напряжении якоря и моменте нагрузки равном номинальному моменту двигателя (приведенном к валу двигателя).
С использованием структурной схемы на рис.5, подав на входы номинальные значения напряжения двигателя и момент сопротивления, получаем переходную характеристику для скорости двигателя в номинальном режиме работы:
Рис.13 Переходная характеристика в номинальном режиме
Результаты моделирования:
При Мс = 4,1652 ω = 293,06
Получаем переходную характеристику для скорости двигателя в режиме холостого хода, с использованием структурной схемы на рис.6
Рис.14 Переходная характеристика в режиме холостого хода
Результаты моделирования:
При Мс = 0 ω = 293,06
Подав на входы схемы, изображенной на рис. 7, номинальные значения момента сопротивления и напряжения питания, получаем переходную характеристику тока в номинальном режиме:
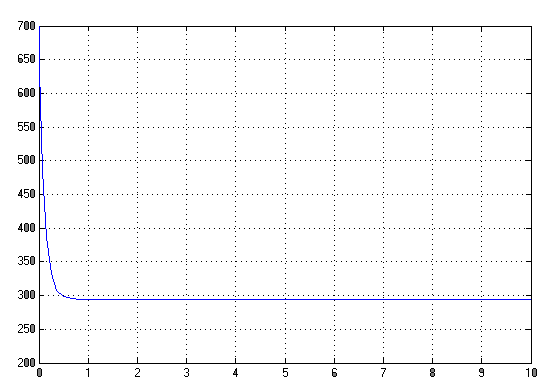
Рис.15 Переходная характеристика тока в номинальном режиме
Результаты моделирования:
При Мс = 4,1652I= 5,85
Выполнив моделирование, структурной схемы на рис.8 определяем ток короткого замыкания:
Рис.16 Ток короткого замыкания
Результаты моделирования:
При Мс = 4,1652I= 700
С использованием структурной схемы на рис.9, подав на входы номинальные значения напряжения двигателя и момент сопротивления, получаем переходную характеристику для скорости двигателя в номинальном режиме работы с учетом инерционности механической и электрической цепи двигателя.
Рис.17 Переходная характеристика в номинальном режиме
Результаты моделирования:
При Мс = 4,1652 ω = 293,06
Получаем переходную характеристику для скорости двигателя в режиме холостого хода, с использованием структурной схемы на рис.10
Рис.18 Переходная характеристика в режиме холостого хода
Результаты моделирования:
При Мс = 0 ω = 293,06
Подав на входы схемы, изображенной на рис. 11, номинальные значения момента сопротивления и напряжения питания, получаем переходную характеристику тока в номинальном режиме с учетом инерционности механической и электрической цепи двигателя:
Рис.19 Переходная характеристика тока в номинальном режиме
Результаты моделирования:
При Мс = 4,1652I= 5,85
Выполнив моделирование, структурной схемы на рис.12 определяем ток короткого замыкания:
Рис.20 Ток короткого замыкания
Результаты моделирования:
При Мс = 8,976I= 550
При сравнении расчетных значений тока и скорости с полученными результатами при моделировании оказалось, что расхождение в них незначительны и погрешность не превышает 0.01% от расчетных значений.
Вывод: В данной лабораторной работе была исследована одномассовая система с приводом постоянного тока. Были составлены уравнения для статического и динамического режимов работы двигателя. Из уравнений для статической работы были определены установившиеся значения скорости и тока, в номинальном режиме и в режиме холостого хода. Также был определен ток короткого замыкания двигателя. Было установлено, что при учете обеих инерционностей двигателя, переходные процессы будут иметь колебательный характер.