Кафедра автоматики и управления в технических системах

ОТЧЕТ

по лабораторной работе №4 по дисциплине

«Электромеханические системы».

Исследование замкнутой одномассовой электромеханической системы.

Москва 2010

Задание

по лабораторной работе № 4

Для одномассовой электромеханической системы со следующими данными:

Номинальная мощность, кВт 1,0

Номинальное напряжение, В 210

Номинальная скорость вращения, об/мин 2800

Номинальный ток, А 5,85

Момент инерции якоря,кг.м² 0.3

Скорость вращения вала

исполнительного механизма, об/мин 240

Момент инерции исполнительного механизма, кг.м² 30

Сопротивление якорной цепи, Ом 0,25

Жёсткость выходного (медленного) вала редуктора, Нм/рад 15000 постоянная времени тиристорного преобразователя, с 0. 03

коэффициент усиления тиристорного преобразователя 20

сопротивление якорной цепи тиристорного преобразователя и индуктивность якорной цепи тиристорного преобразователя принять равными тем же значениям параметров якорной цепи двигателя.

Выполнить моделирование системы тиристорный преобразователь-двигатель, имеющей жёсткую обратную связь по скорости двигателя. При моделировании использовать первый вариант структурной схемы.

1.В структурной схеме для установившегося режима использовать три значения коэффициента передачи обратной связи: 5; 30; 50. Рассчитать значения коэффициента статизма и величину задающего сигнала для этих вариантов.

2.Выполнить моделирование системы с учётом одной и двух иннерционностей. Получить переходные процессы для трёх различных значений коэффициента передачи цепи обратной связи. В схеме с двумя иннерционностями экспериментально найти критическое значение глубины обратной связи.

3.Найденное значение подтвердить расчётом, используя критерий устойчивости Гурвица.

Выполнение.

1. Структурная схема замкнутой одномассовой электромеханической системы в установившемся режиме имеет вид:

Рис.1

Где - коэффициент передачи двигателя по нагрузке, вычисленный с учётом сопротивления тиристорного преобразователя

(1)

Kтп – коэффициент усиления тиристорного преобразователя.

K_д – коэффициент передачи двигателя по управляющему воздействию

U₀ –напряжение задания, вычисленное с учётом коэффициента статизма системы.

Mс – номинальный момент нагрузки,[Нм]

Коэффициент статизма . (2)

Тогда

- напряжение задания тиристорного преобразователя без учёта обратной связи системы.

Для нашего двигателя:

(3)

.

Вычислим коэффициенты статизма для различных значений коэффициента обратных связей:

(4)

Определяем значения напряжений задания тиристорного преобразователя для различных коэффициентов обратной связи:

(5)

Выполняем моделирование нашей замкнутой системы в установившемся режиме при трёх коэффициентах обратной связи:

Рис.2.

При этом график скорости во всех трех случаях имеет вид:

Рис. 3.

Таким образом, при изменении коэффициента обратной связи изменения установившейся скорости двигателя не происходит.

2.Производим моделирование замкнутой системы с учётом одной инерционности.

Схема моделирования представлена на рисунке 3.

Рис.4.

Tтп – постоянная времени тиристорного преобразователя,[с];

Тм - электромеханическая постоянная времени, вычисленная с учётом сопротивления тиристорного преобразователя, [с]

(6)

При моделировании переходных процессов в данной системе уменьшим коэффициенты обратных связей, приведённые в задании в 10 раз и пересчитаем коэффициенты статизма и напряжения задания:

(7)

(8)

Выполняем моделирование нашей замкнутой системы:

Рис. 5.

Полученные графики переходных процессов для заданных значений коэффициента обратной связи представлены ниже:

Kо.с.=1,2

Рис.6

Kо.с.=3

Рис.7

Kо.с.=5,5

Рис.8

Таким образом, на основании полученных графиков делаем вывод, что при учёте одной инерционности переходные процессы имеют устойчивый, колебательный характер. С увеличение коэффициента обратной связи перерегулирование увеличивается.

2. Теперь выполняем моделирование замкнутой системы с учетом двух иннерционностей. Схема моделирования представлена на рисунке 9.

Рис.9.

Где Tэ – электромагнитная постоянная времени системы, [с]

Для моделирования переходных процессов в данной системе производим пересчёт напряжений задания и коэффициентов статизма, так как коэффициенты обратных связей выбираем в 100 раз меньше, чем в задании:

(9)

(10)

Выполняем моделирование нашей замкнутой системы:

Рис. 10.

Полученные переходные процессы в системах представлены ниже:

Kо.с.=0,12

Рис.11.

Kо.с.=0,3

Рис.12.

Kо.с.=0,55

Рис. 13.

Таким образом, из полученных графиков делаем вывод, что введение обратных связей сильно увеличило колебательность системы. Но при данных коэффициентах усиления наша система все еще остается устойчивой. Тогда определяем предельный коэффициент усиления, подбирая его значения:

Рис.14.

4.Определим предельный коэффициент обратной связи, при котором система находится на границе устойчивости. Для этого воспользуемся критерием Гурвица.

Характеристический многочлен замкнутой системы:

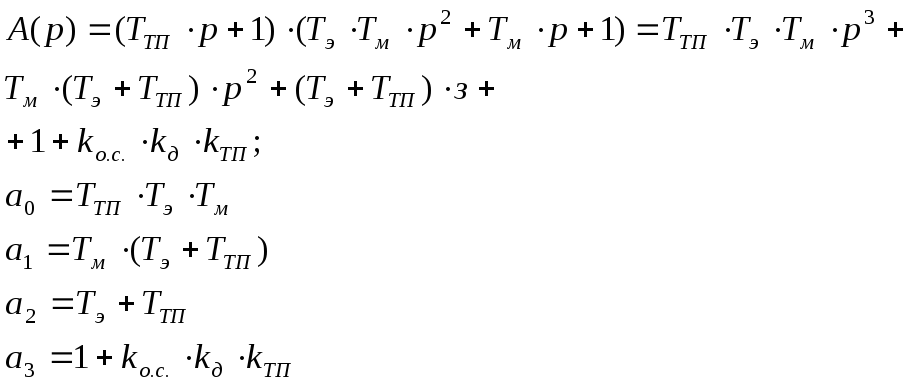(11)

По условию Гурвица:

- система на границе устойчивости.

Отсюда,

(12)

Для нашей системы

Пересчитаем для данного коэффициента обратной связи коэффициент статизма и величину напряжения задания:

(13)

Полученный переходной процесс представлен на рисунке 10:

Рис.15.

Вывод: в данной лабораторной работе мы изучили замкнутую одномассовую электромеханическую систему. Определили экспериментально, что введение обратной связи приводит к увеличению колебательности в системе и при некотором значении коэффициента обратной связи система теряет устойчивость. Определили значение этого коэффициента для нашей системы.