лабораторная работа / лаба 2

Кафедра автоматики и управления в технических системах

ОТЧЕТ

по лабораторной работе №2 по дисциплине

«Электромеханические системы»

Исследование двухмассовой электромеханической системы с электроприводом постоянного тока.

Москва 2010

Задание

по лабораторной работе №2.

Для двигателя постоянного тока независимого возбуждения

с якорным управлением по схеме тиристорный преобразователь - двигатель, соединённого с исполнительным механизмом через редуктор и упругое звено, и имеющих параметры:

Номинальная мощность, кВт 1,0

Номинальное напряжение, В 210

Номинальная скорость вращения, об/мин 2800

Номинальный ток, А 5,85

Момент инерции якоря,кг.м² 0.3

Скорость вращения вала

исполнительного механизма, об/мин 240

Момент инерции исполнительного механизма, кг.м² 30

Сопротивление якорной цепи, Ом 0,25

Жёсткость выходного (медленного) вала редуктора, Нм/рад 15000 постоянная времени тиристорного преобразователя, с 0. 03

коэффициент усиления тиристорного преобразователя 20

сопротивление якорной цепи тиристорного преобразователя и индуктивность якорной цепи тиристорного преобразователя принять равными тем же значениям параметров якорной цепи двигателя.

1.Составить исходную расчётную схему электромеханической системы (момент нагрузки приложен к валу исполнительного механизма).

2.Составить расчётную схему электромеханической системы с приведенными параметрами (момент нагрузки приложен к валу исполнительного механизма).

3.Составить уравнения для динамического режима работы системы (в общем виде и с числовыми коэффициентами),

4.Выполнить моделирование динамических процессов при номинальном напряжении якоря и моменте нагрузки, равном номинальному моменту двигателя (приведенном к валу двигателя).

4.1.Составить структурную схему решения.

4.2.Построить переходные характеристики для ЭДС тиристорного

преобразователя, тока, скорости двигателя, деформации валопровода

4.3.Указать на графиках динамических процессов установившиеся

значения переменных, полученные в результате моделирования.

и сравнить их с расчётными значениями.

5. Выполнить исследование электромеханической системы с использованием пакета Control system toolbox. Математическое описание системы выполнить в подклассе ss. Определить частоты колебаний и степень демпфирования (оператор damp), получить кривые переходных процессов (оператор step) для следующих вариантов:

5.1.В системе тиристорный преобразователь - двигатель(Т - Д),

отсоединённой от исполнительного механизма.

5.2.В механизме, отсоединённом от электропривода.

5.3.В полной двухмассовой электромеханической системе.

5.4.Сравнить полученные значения частот.

6.Привести исходную структурную схему системы с передаточными

функциями (с числовыми значениями параметров системы).

Выполнение.

1. Расчётная схема двухмассовой электромеханической системы (момент нагрузки приложен к валу исполнительного механизма) представлена на рисунке 1.

Рис.1

Составим уравнения, описывающие механическую часть этой системы. Эти уравнения будем составлять в виде уравнений Лагранжа второго род. За обобщённые координаты примем угол поворота вала двигателя _двиг и исполнительного механизма _мех. Запишем выражение для кинетической энергии данной системы:

(1)

В этом выражении J_двиг J_мех – моменты инерции якоря двигателя и исполнительного механизма соответственно.

Вычислим производные от этой энергии:

(2)

Запишем выражения для потенциальной энергии системы. Как известно, потенциальная энергия деформации , где

k – физическая жёсткость медленного вала, ,

- действительная крутильная деформация упругого вала, .

Итак, для системы:

(3)

Вычислим производные от этой энергии:

(4)

- жесткость валопровода, приведённая к валу двигателя.

- угол деформации валопровода, приведённый к валу двигателя.

(5)

Работа обобщённой неконсервативной силы:

(6)

Итак, уравнения для механической части системы:

(7)

2. На основе системы уравнений 7 составляем расчётную схему с приведёнными параметрами:

Рис.2

(8)

- не приведённый момент инерции механизма.

3. Составим уравнения, описывающие данную электромеханическую систему. Для этого добавим к системе 7 уравнения, описывающие электрическую часть этой системы:

(9)

В этих уравнениях:

T_ТП – постоянная времени тиристорного преобразователя, [с];

_ТП – Э.Д.С. тиристорного преобразователя, [В];

K_ТП – коэффициент усиления тиристорного преобразователя;

I – ток якоря двигателя, [А];

R_=R_ТП+R_двиг – суммарное сопротивление тиристорного преобразователя и якоря двигателя, [Ом];

L_=L_ТП+L_двиг - суммарная индуктивность тиристорного преобразователя и якоря двигателя, [Гн];

Се – электрическая постоянная двигателя, ;

_двиг – угол поворота вала двигателя, ;

_мех – угол поворота исполнительного механизма, ;

С_М –механическая постоянная двигателя, ;

 - передаточное число редуктора;

M_c – приведённый момент сопротивления вращению двигателя, ;

- момент инерции якоря двигателя,

- приведённый момент инерции механизма, ;

 - действительная крутильная деформация валопровода, [рад];

- жесткость валопровода, приведённая к валу двигателя, .

Запишем эти уравнения применительно к нашему двигателю:

(10)

(11)

4. Выполним моделирование динамических процессов в системе. Для этого приведём систему уравнений 11 к следующему виду:

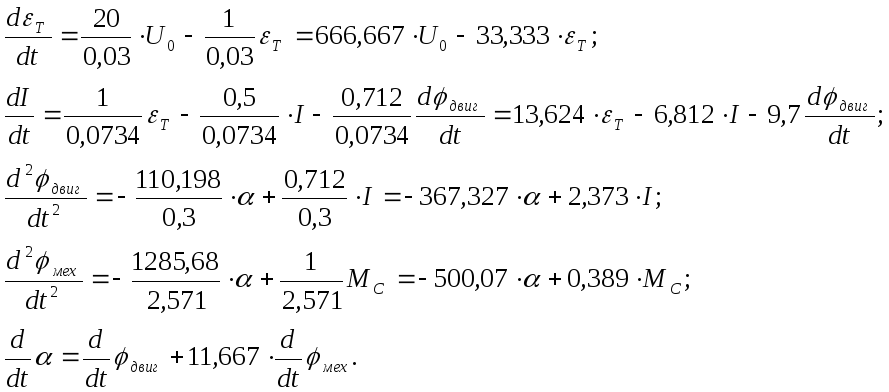(12)

Вычислим величины входных воздействий:

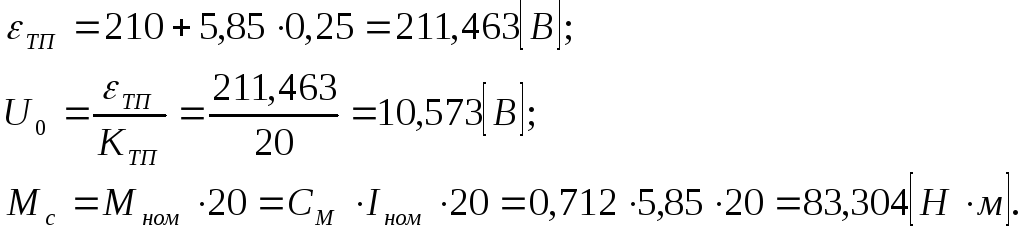(13)

Схема решения системы 12 в Simulink для заданных входных воздействий имеет вид:

Рис.3

В результате моделирования получены следующие графики переходных процессов:

Рис.4 Э.Д.С. тиристорного преобразователя

Рис.5 Ток якоря двигателя

Рис.6 Скорость вращения двигателя

Рис.7 Скорость вращения исполнительного механизма

Рис.8 Деформация валопровода.

5. Выполнить исследование электромеханической системы с использованием пакета Control System Toolbox.

Для этого воспользуемся приложением MATLAB Control System toolbox. Это приложение работает с системой, заданной в пространстве своих координат состояния:

где X - вектор координат состояния системы, U-вектор управления, Y – вектор выхода, A – матрица состояния системы, B – матрица управления системы, C – матрица наблюдения, D –промежуточная матрица.

5.1. Выполним моделирование переходных процессов в системе тиристорный преобразователь – двигатель (Т-Д), отсоединённой от исполнительного механизма.

Это система описывается следующей системой уравнений:

(14)

В этих уравнениях:

T_ТП – постоянная времени тиристорного преобразователя, [с];

_ТП – Э.Д.С. тиристорного преобразователя, [В];

K_ТП – коэффициент усиления тиристорного преобразователя;

I – ток якоря двигателя, [А];

R_=R_ТП+R_двиг – суммарное сопротивление тиристорного преобразователя и якоря двигателя, [Ом];

L_=L_ТП+L_двиг - суммарная индуктивность тиристорного преобразователя и якоря двигателя, [Гн];

Се – электрическая постоянная двигателя, ;

_двиг – угол поворота вала двигателя, ;

С_М –механическая постоянная двигателя, ;

- момент инерции якоря двигателя,

В числовой форме:

(15)

Введём в этой системе координаты состояния:

(16)

Тогда система уравнений в пространстве своих координат состояния запишется следующим образом:

(17)

Обозначив в 17 U₀=U₁ и, учтя масштабирующие коэффициенты входных воздействий, запишем матрицы нашей системы:

(18)

Напишем в MATLAB программу для моделирования переходных процессов в данной системе.

Вводим матрицы нашей системы:

>> A=[-33.333 0 0; 13.624 -6.812 -9.700; 0 2.373 0]

A =

-33.3330 0 0

13.6240 -6.8120 -9.7000

0 2.3730 0

>> B=[7244 ; 0 ; 0]

B =

7244

0

0

>> C=[1 0 0; 0 1 0; 0 0 1]

C =

1 0 0

0 1 0

0 0 1

>> D=0

D =

0

Формируем нашу систему в пространстве своих координат состояния:

>> sys12=ss(A, B, C,D)

a =

x1 x2 x3

x1 -33.33 0 0

x2 13.62 -6.812 -9.7

x3 0 2.373 0

b =

u1

x1 7244

x2 0

x3 0

c =

x1 x2 x3

y1 1 0 0

y2 0 1 0

y3 0 0 1

d =

u1

y1 0

y2 0

y3 0

Определяем собственные числа системы, частоты собственных колебаний и степень демпфирования:

>> damp(sys12)

Eigenvalue (собственные числа)	Damping (степень демпфирования)	Freq. (rad/s) (собственные частоты колебаний)
3.41e+000 + 3.38e+000i -3.41e+000 - 3.38e+000i - ---3.33e+001	7,10e-001 7,10e-001 1.00e+000	4,80e+000 4,80+000 3,33e+000

>> damp(sys12)

Полученные графики имеют вид:

5.2 Выполним моделирование переходных процессов в механизме, отсоединённом от электропривода. Этот механизм описывается следующей системой уравнений:

(19)

В этих уравнениях:

_двиг – угол поворота вала двигателя, ;

_мех – угол поворота исполнительного механизма, ;

 - передаточное число редуктора;

М_двиг – момент, создаваемый двигателем, ,

M_c – приведённый момент сопротивления вращению двигателя, ;

- момент инерции якоря двигателя,

- приведённый момент инерции механизма, ;

 - действительная крутильная деформация валопровода, [рад];

- жесткость валопровода, приведённая к валу двигателя, .

Запишем эти уравнения применительно к нашему двигателю:

(20)

Введем в системе 19 координаты состояния:

(21)

Тогда в пространстве своих координат состояния система запишется следующим образом:

(22)

Обозначив в 22 M_двиг =U₁; M_c=U₂ и, учтя масштабирующие коэффициенты входных воздействий, запишем матрицы нашей системы:

(23)

Запишем программу для моделирования данной системы в MATLAB.

Вводим матрицы нашей системы:

A =

0 0 -367.3270

0 0 499.8000

1.0000 -11.6670 0

>> B=[13.884 0; 0 18.903; 0 0]

B =

13.8840 0

0 18.9030

0 0

>> C=[ 0 0 1]

C =

0 0 1

>> D=0

D =

0

Формируем нашу систему в пространстве своих координат состояния:

>> sys11=ss(A, B,C,D)

a =

x1 x2 x3

x1 0 0 -367.3

x2 0 0 499.8

x3 1 -11.67 0

b =

u1 u2

x1 13.88 0

x2 0 18.9

x3 0 0

c =

x1 x2 x3

y1 0 0 1

d =

u1 u2

y1 0 0

Определяем собственные числа системы, частоты собственных колебаний и степень демпфирования:

>> damp(sys11)

Eigenvalue (собственные числа)	Damping (степень демпфирования)	Freq. (rad/s) (собственные частоты колебаний)
0.00e+000 0.00e+000 + 7.87e+001i 0.00e+000 - 7.87e+001i	-1.00e+00 -6.12e-017 -6.12e-017	0.00e+000 7.87e+001 7.87e+001

Строим переходный процесс в данной системе:

step(sys11)

Рис.12 Деформация валопровода

5.3. Выполняем моделирование двухмассовой системы в целом.

Для этого введём в системе 12 следующие координаты состояния:

(24)

Тогда система 12 запишется следующим образом:

(25)

Обозначив в 25 U₀=U₁; M_c=U₂ и, учтя масштабирующие коэффициенты входных воздействий, запишем матрицы нашей системы:

Запишем программу для моделирования данной системы в MATLAB.

Вводим матрицы нашей системы

>> A=[ -33.333 0 0 0 0; 16.624 -6.812 -9.7 0 0; 0 2.373 0 0 -367.327; 0 0 0 0 42.85; 0 0 1 -11.667 0]

A =

-33.3330 0 0 0 0

16.6240 -6.8120 -9.7000 0 0

0 2.3730 0 0 -367.3270

0 0 0 0 42.8500

0 0 1.0000 -11.6670 0

>> B=[ 7244 0; 0 0; 0 0; 0 18.903; 0 0]

B =

1.0e+003 *

7.2440 0

0 0

0 0

0 0.0189

0 0

>> C=[1 0 0 0 0; 0 1 0 0 0; 0 0 1 0 0; 0 0 0 1 0; 0 0 0 0 1]

C =

1 0 0 0 0

0 1 0 0 0

0 0 1 0 0

0 0 0 1 0

0 0 0 0 1

>> D=0

D =

0

Формируем нашу систему в пространстве своих координат состояния:

>> sys10=ss(A,B,C,D)

a =

x1 x2 x3 x4 x5

x1 -33.33 0 0 0 0

x2 16.62 -6.812 -9.7 0 0

x3 0 2.373 0 0 -367.3

x4 0 0 0 0 42.85

x5 0 0 1 -11.67 0

b =

u1 u2

x1 7244 0

x2 0 0

x3 0 0

x4 0 18.9

x5 0 0

c =

x1 x2 x3 x4 x5

y1 1 0 0 0 0

y2 0 1 0 0 0

y3 0 0 1 0 0

y4 0 0 0 1 0

y5 0 0 0 0 1

d =

u1 u2

y1 0 0

y2 0 0

y3 0 0

y4 0 0

y5 0 0

Определяем собственные числа системы, частоты собственных колебаний и степень демпфирования:

>> damp(sys10)

Eigenvalue (собственные числа)	Damping (степень демпфирования)	Freq. (rad/s) (собственные частоты колебаний)
-3.37e+000 + 1.33e+000i -3.37e+000 - 1.33e+000i -3.70e-002 + 2.96e+001i -3.70e-002 - 2.96e+001i -3.33e+001	9.30e-001 9.30e-001 1.25e-003 1.25e-003 1.00e+000	3.62e+000 3.62e+000 2.96e+001 2.96e+001 3.33e+001

Командой >> step(sys10, 0:0.01: 20) строим переходные характеристики нашей системы:

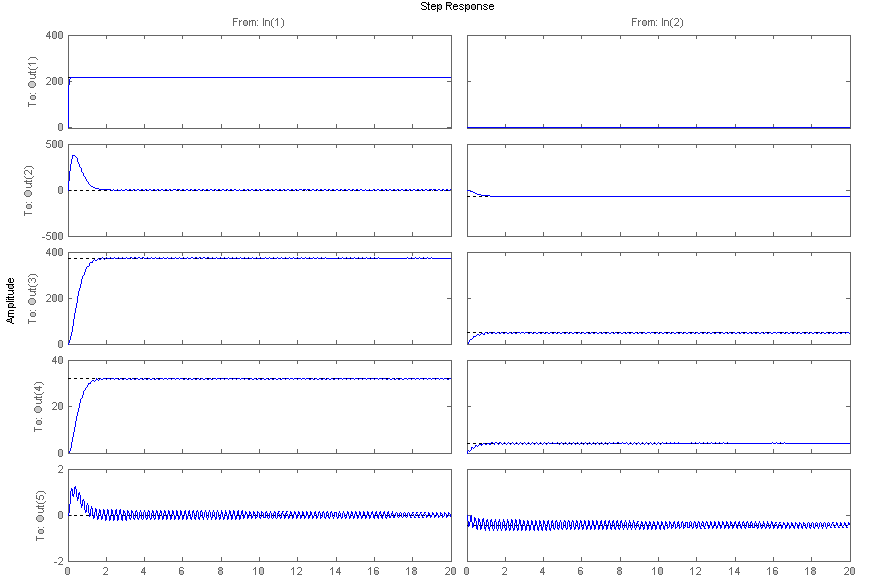
5.4. В ходе моделирования было установлено, что переходные процессы в отдельно рассматриваемых системах тиристорный преобразователь – двигатель и механизм отдельно от двигателя имеют те же частоты, что и соответствующие переходные процессы при рассмотрении электромеханической системы целиком. Это говорит о правильности математического описания нашей электромеханической системы целиком.

6.0. Общий вид структурной схемы двухмассовой электромеханической системы с передаточными функциями представлен на рисунке 18:

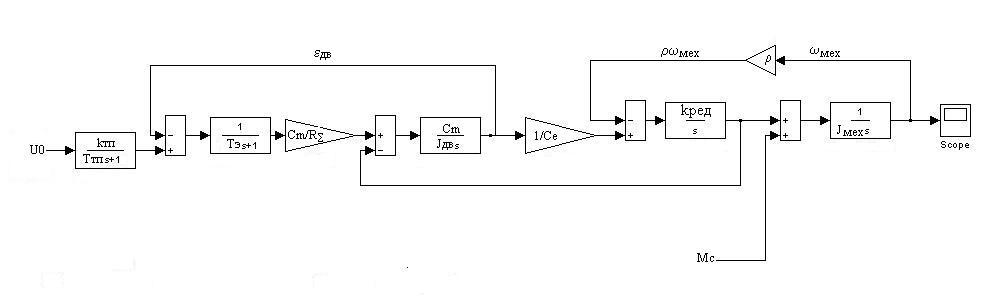
Рис.18.

Для нашей системы нашей системы структурная схема представлена на рисунке 19.

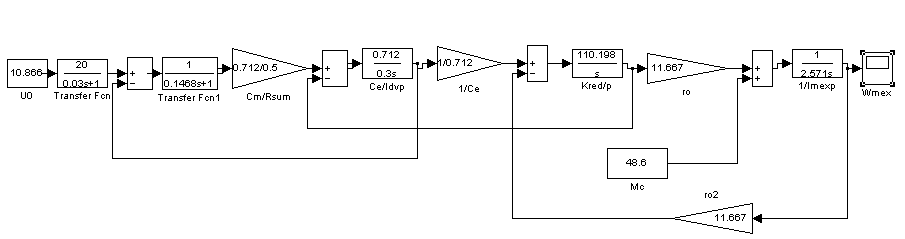
Рис.19

Вывод: в данной лабораторной работе нами изучена двухмассовая электромеханическая система, состоящая из двигателя постоянного тока независимого возбуждения с якорным управлением по схеме тиристорный преобразователь – двигатель, исполнительного механизма, редуктора и упругого звена. Было составлено математическое описание отдельных элементов данной системы и математическая модель системы целиком. Выполнено моделирование переходных процессов в отдельных частях этой системы и в системе в целом. На основании полученных результатов, можно сказать, что переходный процесс в тиристорном преобразователе носит апериодический характер, тогда как переходные процессы в остальных частях системы имеют колебательный вид.

18