Кафедра автоматики и управления в технических системах

ОТЧЕТ

по лабораторной работе №3 по дисциплине

«Электромеханические системы»

Исследование нелинейной двухмассовой разомкнутой системы.

Москва 2010

Задание

по лабораторной работе №3.

Для двигателя постоянного тока независимого возбуждения

с якорным управлением по схеме тиристорный преобразователь - двигатель, соединённого с исполнительным механизмом через редуктор и упругое звено, и имеющих параметры:

Номинальная мощность, кВт 1,0

Номинальное напряжение, В 210

Номинальная скорость вращения, об/мин 2800

Номинальный ток, А 5,85

Момент инерции якоря,кг.м² 0.3

Скорость вращения вала

исполнительного механизма, об/мин 240

Момент инерции исполнительного механизма, кг.м² 30

Сопротивление якорной цепи, Ом 0,25

Жёсткость выходного (медленного) вала редуктора, Нм/рад 15000 постоянная времени тиристорного преобразователя, с 0. 03

коэффициент усиления тиристорного преобразователя 20

сопротивление якорной цепи тиристорного преобразователя и индуктивность якорной цепи тиристорного преобразователя принять равными тем же значениям параметров якорной цепи двигателя.

Приведённый коэффициент вязкого трения упругого звена, Нм/рад/с 5,2

Приведённый кинематический зазор, рад 0,35

Выполнить моделирование электромеханической системы с учётом:

1. нелинейности характеристики тиристорного преобразователя;

2. кинематического зазора в зубчатой передаче редуктора;

3. диссипативных сил в упругом звене;

Форма характеристики тиристорного преобразователя задана таблицей, устанавливающей связь между входной (управляющие ампервитки – AW) и выходной (Э.Д.С. тиристорного преобразователя – E) координатами в относительных единицах (процентах от максимального значения координаты). Точку с координатами AW=37 и E=81 принять за номинальную точку характеристики.

AW	0	20	37	40	60	80	100
E	0	54	81	85.5	96	99	100

1.Составить исходную расчётную схему электромеханической системы (момент нагрузки приложен к валу исполнительного механизма).

2.Составить расчётную схему электромеханической системы с приведенными параметрами (момент нагрузки приложен к валу исполнительного механизма).

3.Составить уравнения для динамического режима работы системы (в общем виде и с числовыми коэффициентами),

4.Выполнить моделирование динамических процессов при номинальном напряжении якоря и моменте нагрузки, равном номинальному моменту двигателя (приведенном к валу двигателя).

4.1.Построить нелинейную характеристику тиристорного преобразователя.

4.2. Составить структурную схему решения с учётом нелинейностей

4.3. Построить переходные характеристики для ЭДС тиристорного

преобразователя, тока, скорости двигателя, деформации валопровода

Выполнение.

1. Расчётная схема двухмассовой электромеханической системы (момент нагрузки приложен к валу исполнительного механизма) представлена на рисунке 1.

Рис.1

Составим уравнения, описывающие механическую часть этой системы. Эти уравнения будем составлять в виде уравнений Лагранжа второго рода. За обобщённые координаты примем угол поворота вала двигателя _двиг и исполнительного механизма _мех. Запишем выражение для кинетической энергии данной системы:

(1)

В этом выражении J_двиг J_мех – моменты инерции якоря двигателя и исполнительного механизма соответственно.

Вычислим производные от этой энергии:

(2)

Запишем выражения для потенциальной энергии системы. Как известно, потенциальная энергия деформации , где

k – физическая жёсткость медленного вала, ,

- действительная крутильная деформация упругого вала, .

Итак, для системы:

(3)

Вычислим производные от этой энергии:

(4)

- жесткость валопровода, приведённая к валу двигателя.

- угол деформации валопровода, приведённый к валу двигателя.

(5)

Работа обобщённой неконсервативной силы:

(6)

Итак, уравнения для механической части системы без учёта диссипативных сил:

(7)

Учтём работу диссипативной силы:

(8)

Заменим перемещение в схеме с приведёнными параметрами

(8)

Тогда

(9)

И окончательно, система уравнений, описывающая механическую часть системы с учетом диссипативной силы, принимает вид:

(10)

2. На основе системы уравнений 10 составляем расчётную схему с приведёнными параметрами:

Рис.2

(11)

- не приведённый момент инерции механизма.

- приведённый коэффициент вязкого трения упругого звена.

3.Составим уравнения, описывающие данную электромеханическую систему. Для этого, вначале, составим уравнение, описывающее тиристорный преобразователь с учётом нелинейности его характеристики. Тиристорный преобразователь описывается уравнением нелинейного инерционного звена:

(12)

Где - обратная характеристика от Э.Д.С. тиристорного преобразователя

(13)

- управляющее ампервитки номинальные. Для нашего случая =

Составим уравнение 12 для нашего тиристорного преобразователя. В предыдущих лабораторных работах получено, что:

Тогда

(14)

(15)

Выполним пересчёт таблицы, описывающий характеристику тиристорного преобразователя из относительных единиц в абсолютные:

0	0
0,54	140,972
0,81	211,459
0,855	223,206
0,96	250,618
0,99	258,449
1,0	261,04

0	0
0,2	58,736
0,37	108,662
0,4	117,472
0,6	176,208
0,8	234,944
1,0	293,68

И окончательно, уравнение, описывающие тиристорный преобразователь, будет иметь следующий вид:

(16)

Теперь запишем систему уравнений, описывающую всю систему в целом с учетом нелинейности характеристики тиристорного преобразователя, диссипативных сил и кинематических зазоров. В общем виде эта система уравнений имеет следующий вид:

(17)

В этих уравнениях:

AWрез – результирующие ампервитки, подаваемые на вход тиристорного преобразователя,

T_ТП – постоянная времени тиристорного преобразователя, [с];

_Т – Э.Д.С. тиристорного преобразователя, [В];

I – ток якоря двигателя, [А];

R_=R_ТП+R_двиг – суммарное сопротивление тиристорного преобразователя и якоря двигателя, [Ом];

L_=L_ТП+L_двиг - суммарная индуктивность тиристорного преобразователя и якоря двигателя, [Гн];

Се – электрическая постоянная двигателя, ;

_двиг – угол поворота вала двигателя, ;

_мех – угол поворота исполнительного механизма, ;

С_М –механическая постоянная двигателя, ;

 - передаточное число редуктора;

M_c – приведённый момент сопротивления вращению двигателя, ;

- момент инерции якоря двигателя,

- приведённый момент инерции механизма, ;

 - действительная крутильная деформация валопровода, [рад];

- жесткость валопровода, приведённая к валу двигателя, ;

_ред – приведенный коэффициент вязкого прения упругого звена, ;

 - приведённый кинематический зазор, .

Запишем эти уравнения применительно к нашему двигателю:

(18)

(19)

4. Выполним моделирование динамических процессов в системе. Для этого приведём систему уравнений 19 к следующему виду:

(20)

4.1.Используя MATLAB, получаем нелинейную характеристику тиристорного преобразователя.

Вычислим величины входных воздействий:

(21)

Схема решения системы 20 в Simulink для заданных входных воздействий имеет вид:

Рис.3

Блок Look-Up-Table используется для задания обратной характеристики тиристорного преобразователя.

В результате моделирования получены следующие графики переходных процессов:

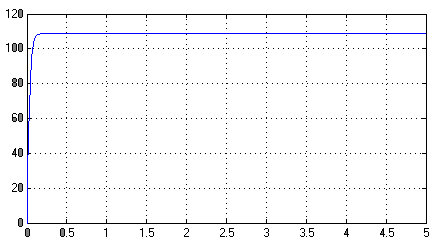
Рис.4 Э.Д.С. тиристорного преобразователя

Рис.5 Ток якоря двигателя

Рис.6 Скорость вращения двигателя

Рис.7 Скорость вращения исполнительного механизма

Рис.8 Деформация валопровода

Вывод: в данной лабораторной работе выполнено исследование электромеханической системы с учётом её нелинейностей. Как и следовало ожидать, полученные переходные процессы отличаются от линейного случая. Если говорить о переходных характеристиках Э.Д.С. тиристорного преобразователя и токе якорной цепи двигателя, то их отличие от линейного случая невелико. Переходные характеристики скоростей двигателя и механизма имеют меньшие установившиеся значения, нежели в линейном случае.