лабораторная работа / Расчет системы управления электроприводом с подчиненным регулированием координат

САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ ТЕХНОЛОГИИ И УПРАВЛЕНИЯ

ФАКУЛЬТЕТ ИНЖЕНЕРНО – СТРОИТЕЛЬНЫЙ

КАФЕДРА «УПРАВЛЕНИЕ И ИНФОРМАТИКА В ТЕХНИЧЕСКИХ СИСТЕМАХ»

Практическая работа №2

по дисциплине:

Электромеханические системы

Расчет системы управления электроприводом

с подчиненным регулированием координат

Выполнили ст. гр. УИТ-52

Телегин Е.Г.____________

Принял преподаватель

Мефедова Ю.В.__________

«____» ____________ 2008г.

Балаково 2008

Цель работы:

Расчет двухконтурной системы управления электроприводом постоянного тока с подчиненным регулированием координат.

Исходные данные.

Силовая часть электропривода представляет собой систему тиристорный преобразователь – двигатель постоянного тока с независимым возбуждением.

Номинальные напряжения, ток, момент и скорость двигателя:

U_НОМ=60 В, I_НОМ=2.27 А, М_НОМ=0,49 Н·м, ω_НОМ=209 рад/с.

Сопротивление и индуктивность якоря и момент инерции двигателя:

R_Я=0,94 Ом, L_Я=0,038 Гн, J=0,00153 кг·м².

Коэффициент усиления и постоянная времени преобразователя:

k_П=50, Т_П=Т_μ=0,008 с.

Передаточный коэффициент тахогенератора (обратная связь по скорости):

k_ТГ= k_ОС=0,024 В·с/рад.

Передаточный коэффициент обратной связи по току:

k_ОТ =1,47 В/А.

Решение.

1) Рассчитаем недостающие параметры.

Коэффициент ЭДС k_Е:

, В·с.

Коэффициент момента k_М:

, Н·м А^-1.

Электромагнитная постоянная времени двигателя:

с.

Механическая постоянная времени двигателя:

с.

Вспомогательный коэффициент k₀:

, А/В.

2) Настроим внутренний контур тока на технический оптимум. Передаточная функция регулятора тока согласно (9):

.

Передаточная функция замкнутого контура, согласно (11):

.

Исследование внутреннего контура с регулятором и без, осуществляется самостоятельно, путем построения переходных процессов и логарифмических амплитудно-частотных характеристик.

3) Настроим внешний контур скорости на технический и симметричный оптимум. Передаточная функция регулятора скорости, настроенного на ТО, согласно (13):

.

Передаточная функция регулятора скорости, настроенного на СО, согласно (16):

.

4) Исследуем систему управления электропривода. На рис.1 представлены переходные процессы системы ( h(t) – без регулятора скорости, hrs1(t) – с регулятором, настроенным на ТО, hrs2(t) – с регулятором, настроенным на СО). На рис.2 соответственно представлены логарифмические амплитудно-частотные характеристики (ЛАЧХ). По построенным графикам определяются все характеристики и делаются выводы о влиянии на качество процессов регуляторов, настроенных на технический и симметричный оптимум.

Рис.1. Переходные процессы внешнего контура скорости

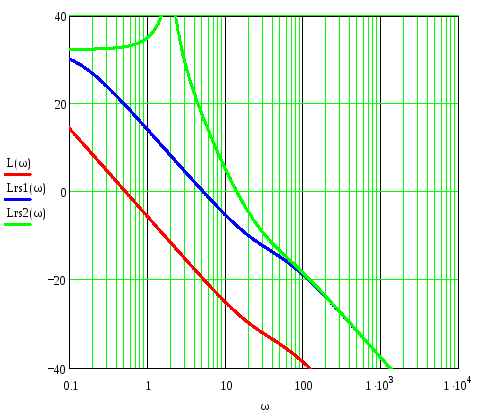
Рис.2. ЛАЧХ внешнего контура скорости

5) Определим параметры ПИ-регуляторов.

Параметры усилительного и интегрирующего звеньев ПИ-регулятора тока, равны соответственно: k_П=0,032313, Т_И=1,251. Зададимся значением емкости С=1 мкФ, тогда с учетом (18):

кОм, кОм.

Параметры усилительного и интегрирующего звеньев ПИ-регулятора скорости, равны соответственно: k_П=9,8182, Т_И=3,3·10^-3. Зададимся значением емкости С=0,5 мкФ, тогда с учетом (18):

кОм, кОм.

Вывод:

В ходе выполнения данной работы был произведен расчет двухконтурной системы управления электроприводом постоянного тока с подчиненным регулированием координат. В результате по переходным характеристикам было установлено, что система без регулятора находится в неопределенном состоянии, а системы с регулятороми достигают установившегося состояния за 22 с, причем перерегулирование в системе при настройке контура тока на технический оптимум уменьшается в ≈2 раза по сравнению с настройкой на симметричный оптимум. Также по ЛАЧХ было установлено, что с регулятором, система имеет более широкую полосу пропускания, а следовательно меньшее время переходного процесса контура.