
контрольная работа / Контрольная работа по ЭМ
.pdfКонтрольная работа по электромеханике
Вариант №

Задача 1 (варианты 01-100). Для трехфазного трансформатора,
параметры которого приведены в табл.1, определить коэффициенты трансформации; номинальные токи в обмотках трансформатора;
параметры Т- образной схемы замещения, угол магнитных потерь δ.
Построить внешние характеристики U2 = f(β) для cos ϕ2 = 1 и cos ϕ2 = 0,8 (для нечетных вариантов ϕ2 > 0, для четных - ϕ2 < 0), задаваясь следующими значениями коэффициента нагрузки β = 0; 0,25; 0,5; 0,75; 1,0; 1,25. Определить характер нагрузки (величину и знак фазового угла
ϕ2), при котором напряжение U2 на зажимах вторичной обмотки не будет зависеть от коэффициента нагрузки β и для этого случая построить график зависимости КПД от нагрузки η = f(β) при изменении β от 0 до 1,25 через 0,25. Начертить электрическую схему соединения обмоток трансформатора /1-4; 7-9; 12/ и векторную диаграмму напряжений, соответствующую заданной группе соединения.
Исходные данные трехфазных трансформаторов
Номинальная |
Напряжения |
Схема и |
Ток |
Напряжение |
Мощность |
Мощность |
мощность |
ВН/НН, кВ |
группа |
холостого |
к.з., uк, % |
холостого |
к.з. Рк, |
Sном., |
соед. |
хода |
|
хода Ро, |
||
|
|
|
||||
кВ × А |
|
обмоток |
i0, % |
|
Вт |
Вт |
|
|
|
|
|||
|
|
|
|
|
|
|
1600 |
35 / 13,8 |
- 5 |
1,3 |
6,5 |
3200 |
14500 |
|
|
|
|
|
|
|
Решение:
Определим коэффициент трансформации для трансформатора:
k = U1ном = 35 = 2,54. U2ном 13,8
Номинальные линейные токи вычислим по номинальной мощности трансформатора:
I2ном = |
S |
×103 |
= |
1600 ×103 |
= 66,94(А). |
|||||
|
ном |
|
|
|
|
|||||
|
|
|
|
|
|
|
||||
3 × |
3 ×13,8 ×103 |
|||||||||
|
U2ном |
|
||||||||
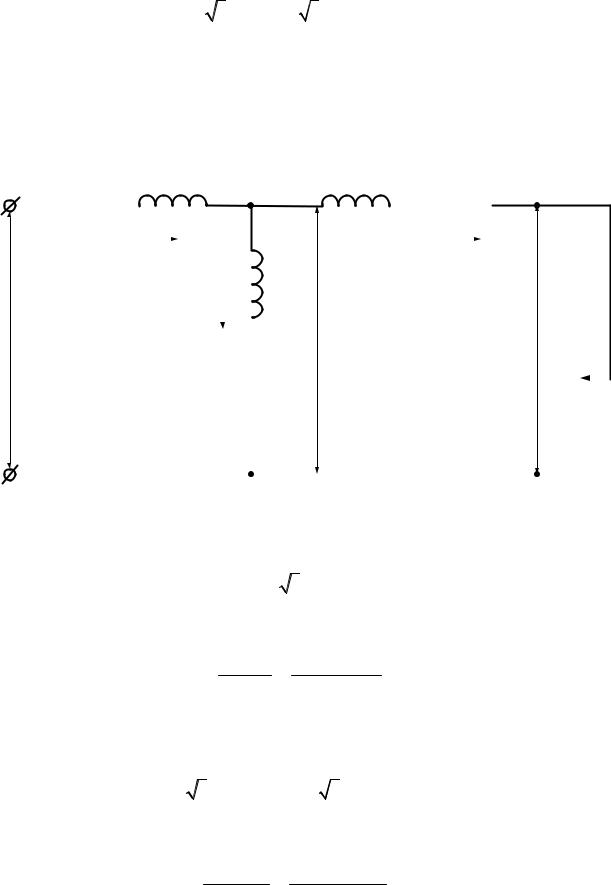
Представим электрическую схему замещения приведённого трансформатора
на рис.1.1:
Рис.1.1. Электрическая схема замещения приведённого трансформатора
|
R |
1 |
|
X |
|
′ |
R′ |
||||
|
|
|
1 |
X2 |
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɺI1 |
ɺ |
|
|
|
Xm |
−ɺI = ɺI − ɺI |
|||||||
|
I0 |
|
|
|
|
2 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɺ |
|
|
|
|
|
|
|
ɺ′ |
|||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||
U1 |
|
|
|
|
|
|
|
−U2 |
|||||
|
|
|
|
|
ɺ |
ɺ′ |
|
|
|
|
|
|
|
|
|
|
|
|
Rm −E1 |
= E2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|||
|
|
|
|
|
|
|
|
|
|
|
|
Zн |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Номинальное фазное напряжение на стороне обмоток НН:
U2 Ф |
= |
13800 |
= 7967, 4В. |
||
|
|
|
|||
|
|||||
|
3 |
|
|
||
Определим параметры схемы замещения; ток холостого хода равен:
I0ном = i0 × I2ном = 1,3% × 66,94 = 0,87А. 100% 100%
Коэффициент мощности при режиме холостого хода:
cos j0 |
= |
|
|
|
P0 |
|
= |
|
14500 |
» 0, 27. |
|
|
|
|
× U1ном |
|
|
|
|
||||
|
3 |
× I0ном |
3 × 35000 × 0,87 |
|
|||||||
Номинальное напряжение в режиме короткого замыкания равно:
U1К = uК × U1ном = 6,5% ×35000 = 2275 В. 100% 100%

Ток короткого замыкания обмотки НН трансформатора:
I |
= I |
= |
S |
×103 |
= |
1600 × |
103 |
= 26, 4(А). |
||||
|
ном |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||
1K |
1ном |
|
|
3 × U |
3 ×35 |
×103 |
|
|||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
1ном |
|
|
|
|
|
|
Коэффициент мощности в режиме короткого замыкания:
cos jK |
= |
|
|
|
PK |
|
= |
|
14500 |
|
» 0,14; |
|
|
|
|
|
|
|
|
|
|
||||
|
3 |
× U1K |
× I1K |
3 × 2275 × |
26, 4 |
|
||||||
jK = 81,9 ; sinjK = 0,99
Полное сопротивление при коротком замыкании:
ZK |
= |
|
UK |
= |
|
2275 |
» 49,75 |
Ом. |
||||
|
|
|
|
|
|
|
||||||
3 |
× I1К |
3 × 26, 4 |
||||||||||
|
|
|
|
|
|
|
||||||
Активная составляющая сопротивления короткого замыкания равна:
R K = ZK × cos jK = 49,75 × 0,14 » 6,96 Ом.
Индуктивная составляющая сопротивления короткого замыкания равна:
XK = ZK × sin jK = 49,75 × 0,99 = 49, 25 Ом.
Считаем, что схема замещения на рис. 1.1 является симметричной
R1 = R′2 ; X1 = X′2 .
Тогда приведённые активные и индуктивные сопротивления Т- образной
схемы замещения:
R1 |
= R¢2 |
= |
R K |
= |
6,96 |
= 3,48 Ом |
||||||
|
|
|
|
|||||||||
|
|
|
2 |
2 |
|
|
||||||
X = X¢ |
= |
XK |
|
= |
49,25 |
= 24,62 Ом. |
||||||
|
|
|||||||||||
1 |
2 |
|
2 |
|
2 |
|
|
|||||
|
|
|
|
|
|
|||||||
Фактические значения сопротивления вторичной обмотки трансформатора:
R |
|
= |
R′2 |
= |
3, 48 |
= 0,54 Ом |
2 |
k2 |
|
||||
|
|
2,542 |
|
|||

X = X′2 = 24,62 = 3,82 Ом. 2 k2 2,542
Коэффициент мощности в режиме холостого хода:
cos j0 |
= |
|
|
|
P0 |
|
= |
|
3200 |
» 0,06; |
|
|
|
|
× I0ном |
|
|
|
|
||||
|
3 |
× U1ном |
3 × 0,87 ×35000 |
|
|||||||
j0 = 86,52 ; sinj0 = 0,998.
Полное сопротивление ветви намагничивания схемы замещения трансформатора:
Zm = |
|
|
U1ном |
|
= |
35000 |
|
= 23226,7 Ом. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
3 × I0 ном |
3 × 0,87 |
||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||
Активное сопротивление ветви намагничивания: |
|
|
|||||||||||||||
R m = Zm × cos j0 |
= 23226,7 × 0,06 = 1393,6 Ом. |
||||||||||||||||
Индуктивное сопротивление цепи намагничивания: |
|||||||||||||||||
Xm = Zm ×sinj0 = 23226,7 × 0,998 = 23180, 2 Ом. |
|||||||||||||||||
Для расчёта КПД воспользуемся выражением: |
|
|
|||||||||||||||
h = |
|
|
|
|
|
b ×SНОМ × cos j2 |
|
. |
|||||||||
b ×S |
НОМ |
× cos j |
2 |
+ P |
ном |
+ b2 |
× P |
||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
к.ном |
||||||
Задавшись значениями коэффициента нагрузки: b = 0; 0,25; 0,5; 0,75; 1,0; 1,25, рассчитаем для каждого из них КПД сначала для коэффициента мощности нагрузки cos j2 = 1, потом cos j2 = 0,8.
Коэффициент нагрузки, соответствующий максимальному КПД равен:
b¢ = |
P0 ном |
= |
|
3200 |
= 0,47. |
|
|
||||
|
Pк.ном |
14500 |
|
||
Максимальное значение КПД, при cos ϕ2 = 1:

hmax |
= |
b′×SНОМ × cos j2 |
= |
0, 47 ×1600 ×1 |
= 0,99. |
|||||
b¢ ×SНОМ |
× cos j2 |
+ 2 × P0ном |
0, 47 |
×1600 ×1 + |
2 ×3, 2 |
|||||
|
|
|
|
|||||||
Максимальное значение КПД, при cos ϕ2 = 0,8:
hmax |
= |
b′×SНОМ × cos j2 |
= |
0, 47 ×1600 × 0,8 |
= 0,989. |
|||||
b¢ ×SНОМ |
× cos j2 |
+ 2 × P0ном |
0,47 |
×1600 × 0,8 |
+ 2 ×3, 2 |
|||||
|
|
|
|
|||||||
Результаты расчётов приведём ниже, в табл.1.1:
Табл.1.1. Зависимость КПД от коэффициента нагрузки трансформатора при
разных значениях коэффициента мощности ( cos ϕ2 =1; cos ϕ2 |
= 0,8.) |
||||||
|
|
|
|
|
|
|
|
β |
0 |
0,25 |
0,5 |
0,75 |
1 |
|
1,25 |
|
|
|
|
|
|
|
|
η(при cosϕ2 =1) |
0 |
0,99 |
0,992 |
0,991 |
0,989 |
|
0,987 |
|
|
|
|
|
|
|
|
η(при cosϕ2 = 0,8) |
0 |
0,985 |
0,988 |
0,986 |
0,984 |
|
0,981 |
|
|
|
|
|
|
|
|
Рис.1.2. Зависимость η = f (β) трансформатора при cos ϕ2 |
=1; cos ϕ2 = 0,8 |
|||
1 |
|
|
|
|
0.99 |
|
|
|
|
η1 (β ) 0.98 |
|
|
|
|
η2 (β ) |
|
|
|
|
0.97 |
|
|
|
|
0.96 |
|
|
|
|
0.95 |
0.313 |
0.625 |
0.938 |
1.25 |
0 |
||||
|
|
β |
|
|
Из анализа полученных результатов на рис. 1.2 и табл.1.1. следует: КПД |
||||

трансформатора при чисто активной нагрузке ( cos j2 = 1) выше, чем при
активноиндуктивной (cos j2 = 0,8)на всём диапазоне значений β.
Для построения внешних характеристик найдём активную и индуктивную
составляющие напряжения короткого замыкания:
UKA = I1КА × R K = 26, 4 × 6,96 = 183,74 В
UKР = I1КР × XK = 26,4 × 49,25 =1,3 ×103 В.
Активная составляющая напряжения короткого замыкания в %:
uка |
= |
UKA |
×100% = |
183,74 |
×100% = 0,525%. |
U1ном |
|
||||
|
|
35000 |
|
||
Реактивная составляющая напряжения короткого замыкания в %:
uкр = UKР ×100% = 1300 ×100% = 3,715%. U1ном 35000
Номинальное изменение вторичного напряжения трансформатора в %:
DUНОМ = b(uка × cos j2 + uкр × sin j2 ).
Номинальное изменение вторичного напряжения трансформатора в вольтах:
DU |
Н |
= |
UНОМ × U |
. |
|
|
|
100% |
1ном |
|
|
|
|
|
|
|
|
Вторичное напряжение трансформатора равно:
U2 = U2 НОМ − UH .
Произведём расчёт вторичного напряжения трансформатора при cos ϕ2 =1
и cos ϕ2 = 0,8 ; задаваясь различными значениями коэффициентов нагрузки:
β = 0; 0,25; 0,5; 0,75; 1,0; 1,25. Результаты расчёта сведём в табл. 1.2.

Табл.1.2. Зависимость вторичного напряжения трансформатора U2 от
коэффициента нагрузки β при разных значениях коэффициента
|
мощности ( cos ϕ2 =1; cos ϕ2 |
= 0,8.) |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
β |
|
0 |
0,25 |
|
0,5 |
|
0,75 |
1 |
1,25 |
|
|
|
|
|
|
|
|
|
|
||
U2 (cos ϕ2 |
=1) ,В |
1,38 ×104 |
1,375 ×104 |
|
1,371×104 |
1,366 ×104 |
1,362 ×104 |
1,357 ×104 |
||
|
|
|
|
|
|
|
|
|
|
|
U2 (cos ϕ2 |
= 0,8) |
1,38 ×104 |
1, 401×104 |
1, 422 ×10 |
4 |
1, 443 ×104 |
1, 463 ×104 |
1, 484 ×10 |
4 |
|
В |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U,% |
0 |
0,131 |
|
0,262 |
|
0,394 |
0,525 |
0,656 |
|
|
|
|
|
|
|
|
|
|
|
|
|
U,B |
0 |
45,936 |
|
91,872 |
|
137,808 |
183,744 |
229,68 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Построим внешние характеристики трансформатора U2 = f (β) (рис.1.3). |
|
||||||
Рис.1.3. Внешние характеристики трансформатора при cos ϕ2 |
= 0,8; cos ϕ2 |
=1; |
|||||
cos ϕ2 = 0,93. |
|
|
|
|
|
|
|
|
1.49×104 |
|
|
|
|
|
|
|
1.452×104 |
|
|
|
|
|
|
U2(β ) |
1.414×104 |
|
|
|
|
|
|
u2(β ) |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
u3(β ) |
1.376×10 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.338×104 |
|
|
|
|
|
|
|
1.3×104 |
0.313 |
0.625 |
0.938 |
1.25 |
|
|
|
|
0 |
|
||||
|
|
|
|
β |
|
|
|
На рис.1.3 построены графики внешних характеристик при cos ϕ2 = 0,8 |
|
||||||
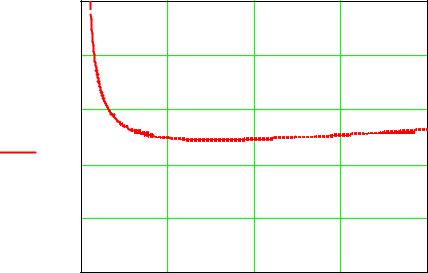
(график синего цвета); при cos ϕ2 = 1(график красного цвета). Опытным путём нашли фазовый угол ϕ2 , при котором напряжение U2 на зажимах вторичной обмотки практически не зависит от коэффициента нагрузки β,
который равен: ϕ2 = 21,85 . Построим для данного значения фазового угла график зависимости КПД от нагрузки η= f(β) при изменении β от 0 до 1,25
(см. рис.1.4). На рис.1.3. график характеристики при ϕ2 = 21,85
(cos ϕ2 = 0,93) показан коричневой линией, параллельной оси β. Характер нагрузки – активно-индуктивный.
Рис.1.4. Зависимость η = f (β) трансформатора при cos ϕ2 = 0,93.
1.07
1.046
1.022
η (β )
0.998
0.974
0.95
0 |
0.313 |
0.625 |
0.938 |
1.25 |
β
Данный тип трансформатора соответствует группе соединения – 5
«звезда – треугольник » (рис. 1.5). Поэтому построим векторную диаграмму в соответствии с данной группой соединения с целью определения ЭДС
обмоток (рис.1.6). Для этого найдём комплексные величины напряжений,
ЭДС и тока трансформатора для фазы А и В. Линейное напряжение
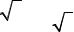
первичной обмотки:
Uɺ1 = Uɺ AB = U1ном × ej×30 = 35000(cos30 + j×sin 30 )=
= 35000(0,866 + 0,5j)= 30310 +17500 j (B).
Отношение линейных напряжений для данной группы соединения равно:
ɺ |
|
|
ɺ |
|
|
w |
|
3 |
|
|
|
U |
1 |
= |
U |
AB |
= |
1 |
= k 3. |
||||
ɺ |
|
ɺ |
|
w2 |
|
||||||
U2 |
|
Uab |
|
|
|
|
|||||
Отсюда линейное напряжение на вторичной обмотке равно:
ɺ |
= U1ном × e |
j(30 -150 ) |
= -6900 -11950,8 × j =13800(-0,5 - j× 0,866)=13800 × e |
- j×120 |
U2 |
|
(В). |
Комплексное значение приведённого напряжения вторичной обмотки:
ɺ |
ɺ |
ɺ |
× k = 2,54 ×13800 × e |
- j120 |
= 35052 |
× (-0,5 |
- 0,866 j) = |
U¢2 |
= U¢ab |
» U2 |
|
= -17526 - 30355j = 35052 × е- j×120 (В).
Приведённое полное сопротивление вторичной обмотки трансформатора:
Zɺ¢2 = R¢2 + jX¢2 = 3, 48 + j× 24,62 (Ом).
Комплексное значение приведённого тока вторичной обмотки:
ɺ |
|
ɺ |
|
-17526 - 30355 × j |
|
3 |
|
|
|
U¢2 |
|
|
|
|
|||
I¢2 |
= |
|
= |
3,48 + j × 24,62 |
= -1,307 ×10 |
|
+ 527,026 |
× j = |
Zɺ¢ |
|
|||||||
|
|
2 |
|
|
|
|
|
|
=1409, 26(0,927 + 0,374 j)=1409, 26 × еj×22 |
(А). |
|
||||||
Комплексное значение тока первичной обмотки:
