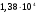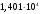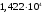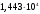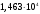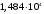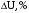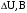1,0; 1,25, Рассчитаем для каждого из них кпд сначала для коэффициента мощности нагрузки , потом
Коэффициент нагрузки, соответствующий максимальному КПД равен:
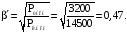
Максимальное
значение КПД, при
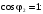
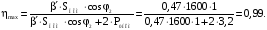
Максимальное
значение КПД, при
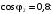
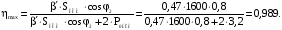
Результаты расчётов приведём ниже, в табл.1.1:
Табл.1.1. Зависимость КПД от коэффициента нагрузки трансформатора при
разных
значениях коэффициента мощности (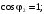
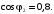 )
)
|
β |
0 |
0,25 |
0,5 |
0,75 |
1 |
1,25 |
|
|
0 |
0,99 |
0,992 |
0,991 |
0,989 |
0,987 |
|
|
0 |
0,985 |
0,988 |
0,986 |
0,984 |
0,981 |
Рис.1.2.
Зависимость
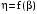 трансформатора
при
трансформатора
при
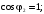
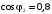
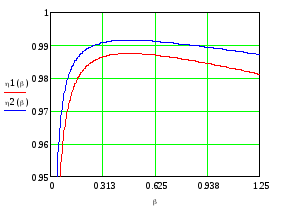
Из анализа полученных результатов на рис. 1.2 и табл.1.1. следует: КПД
трансформатора
при чисто активной нагрузке (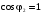 )
выше, чем при
)
выше, чем при
активно-
индуктивной
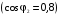 на
всём диапазоне значений β.
на
всём диапазоне значений β.
Для построения внешних характеристик найдём активную и индуктивную
составляющие напряжения короткого замыкания:
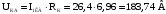
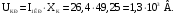
Активная составляющая напряжения короткого замыкания в %:
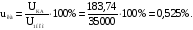
Реактивная составляющая напряжения короткого замыкания в %:
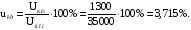
Номинальное изменение вторичного напряжения трансформатора в %:
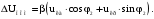
Номинальное изменение вторичного напряжения трансформатора в вольтах:
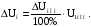
Вторичное напряжение трансформатора равно:
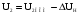 .
.
Произведём
расчёт вторичного напряжения трансформатора
при
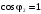
и
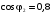 ;
задаваясь различными значениями
коэффициентов нагрузки:
;
задаваясь различными значениями
коэффициентов нагрузки:
β = 0; 0,25; 0,5; 0,75; 1,0; 1,25. Результаты расчёта сведём в табл. 1.2.
Табл.1.2.
Зависимость вторичного напряжения
трансформатора
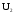 от
от
коэффициента нагрузки β при разных значениях коэффициента
мощности
(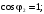
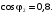 )
)
|
β |
0 |
0,25 |
0,5 |
0,75 |
1 |
1,25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0,131 |
0,262 |
0,394 |
0,525 |
0,656 |
|
|
0 |
45,936 |
91,872 |
137,808 |
183,744 |
229,68 |
Построим
внешние характеристики трансформатора
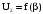 (рис.1.3).
(рис.1.3).
Рис.1.3.
Внешние характеристики трансформатора
при
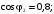
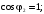
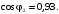
На
рис.1.3 построены графики внешних
характеристик при
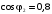
(график
синего цвета); при
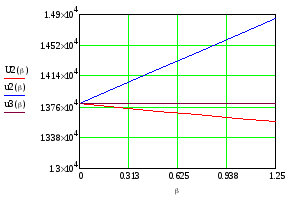
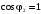 (график
красного цвета). Опытным путём нашли
фазовый угол
(график
красного цвета). Опытным путём нашли
фазовый угол
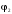 ,
при котором напряжение
,
при котором напряжение
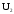 на
зажимах вторичной обмотки практически
не зависит от коэффициента нагрузки β,
который равен:
на
зажимах вторичной обмотки практически
не зависит от коэффициента нагрузки β,
который равен:
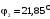 .
Построим для данного значения фазового
угла график зависимости КПД от нагрузки
.
Построим для данного значения фазового
угла график зависимости КПД от нагрузки
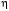 =
f(β) при изменении β от 0 до 1,25 (см.
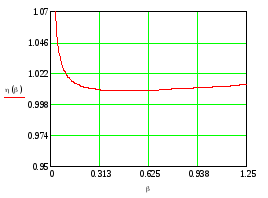
рис.1.4). На рис.1.3. график характеристики
при
=
f(β) при изменении β от 0 до 1,25 (см.
рис.1.4). На рис.1.3. график характеристики
при
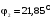
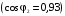 показан коричневой линией, параллельной
оси β. Характер нагрузки – активно-индуктивный.
показан коричневой линией, параллельной
оси β. Характер нагрузки – активно-индуктивный.
Рис.1.4.
Зависимость
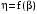 трансформатора
при
трансформатора
при
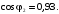
Данный тип трансформатора соответствует группе соединения – 5
«звезда –треугольник » (рис. 1.5). Поэтому построим векторную диаграмму
в соответствии с данной группой соединения с целью определения ЭДС
обмоток (рис.1.6). Для этого найдём комплексные величины напряжений,
ЭДС и тока трансформатора для фазы А и В. Линейное напряжение
первичной обмотки:
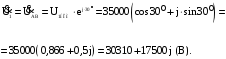
Отношение линейных напряжений для данной группы соединения равно:
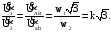
Отсюда линейное напряжение на вторичной обмотке равно:
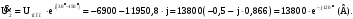
Комплексное
значение приведённого напряжения
вторичной обмотки:
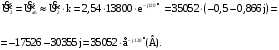
Приведённое полное сопротивление вторичной обмотки
трансформатора:
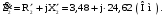
Комплексное значение приведённого тока вторичной обмотки:
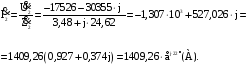
Комплексное значение тока первичной обмотки:
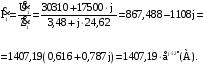
Комплексное значение тока холостого хода равно:
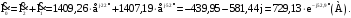
Угол
магнитных потерь
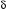 определяется из
формулы для комплексного
определяется из
формулы для комплексного
значения тока холостого хода:
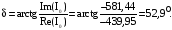
Фазовый угол между векторами напряжения и тока вторичной обмотки
равен:
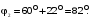 Вектор
приведённой вторичной ЭДС
Вектор
приведённой вторичной ЭДС
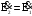
получается
геометрическим сложением вектора
напряжения
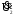 с
с
падениями напряжения во вторичной обмотке:
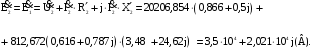
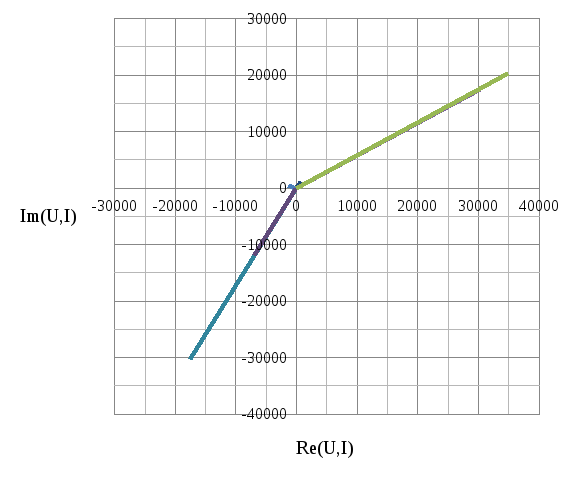
Построим векторную диаграмму напряжений (рис.1.6)
Рис.1.5. Схема соединения обмоток для группы – 5 «звезда –
треугольник»
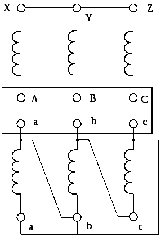
Рис.1.6. Векторная диаграмма напряжений трансформатора
Задача 2. Для трехфазного асинхронного двигателя с фазным ротором,
параметры которого заданы в таблице1.2, определить номинальные
момент Мн и скольжение sн, критический момент Мк, перегрузочную
способность и критическое скольжение sк. Пользуясь формулой
Клосса для скольжений s = 1; 0,8; 0,6; 0,4; 0,2; sк; sн; 0, построить
естественную и две искусственные механические характеристики с
разными величинами сопротивлений добавочных резисторов в цепи
ротора (Rдоб = R2 и Rдоб = 4 R2, где R2 – активное сопротивление фазы
обмотки ротора). Пренебрегая величиной X2, определить величину R2, а
затем рассчитать и построить зависимость скольжения от тока ротора
s = f(I2). Определить диапазон изменения частоты вращения при
реостатном регулировании для статического момента, равного
номинальному (Мс = Мн). Двигатель подключен к сети с линейным
напряжением 380В при схеме соединения фаз статора звездой.
Табл.1.2.

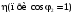
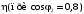
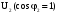 ,В
,В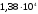
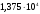
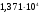
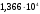
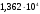
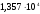
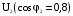 В
В