6. Законы композиции

6.1. Композиция объектов. Таблица Кэли.

В математике и ее приложениях боль­шое значение имеют отношения, ставящие в соответствие паре каких-либо объектов (а, b) третий объект с. Примерами таких отношений являются действия над числами. В общем случае отношение может представлять собой некоторую операцию не только между числами, но и между объектами любой природы. Запись a┬b=c (a┴b=c) означает, что а в композиции c b дает с. Символ ┬ (┴) обозначает операцию, объекты а и b называют операндами, а объект с – результатом операции или композицией объектов а и b.

Обозначим множества операндов соответственно через А и В (aA, bB), а множество результатов операции — через С (сС). Так как множество всех пар (а, b) есть прямое произведение , то операцию определяют как отображение множества в С, т. е. , и часто называют законом композиции.

Любой закон композиции над конечными множествами можно задавать прямоугольной матрицей (таблицей Кэли). Строки таблицы соответствуют элементам множества А, столбцы - элементам множества В. На пересечении строки и столбца, соответствующих паре (а, b), располагается элемент с= a┬b. Хорошо известными примерами являются таблицы сложения и умножения одноразрядных чисел. В общем случае таблица, опре­деляющая бинарную операцию, имеет вид:

┬				…
				…
				…
				…
…	…	…	…	…

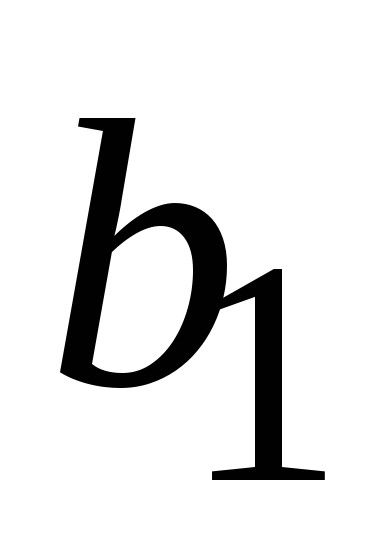
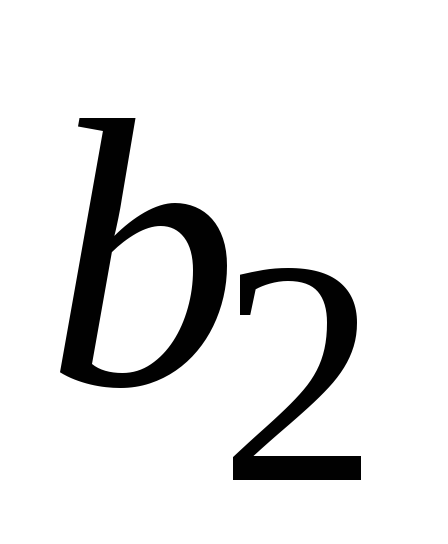
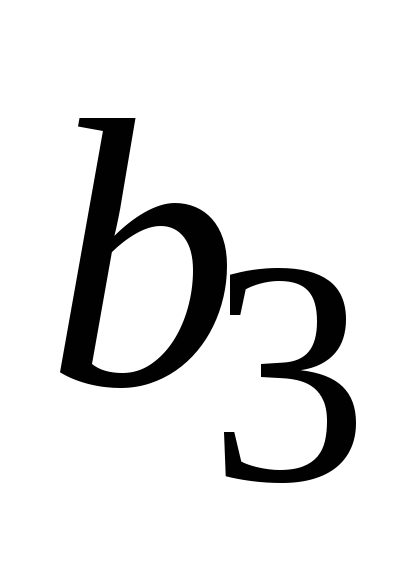
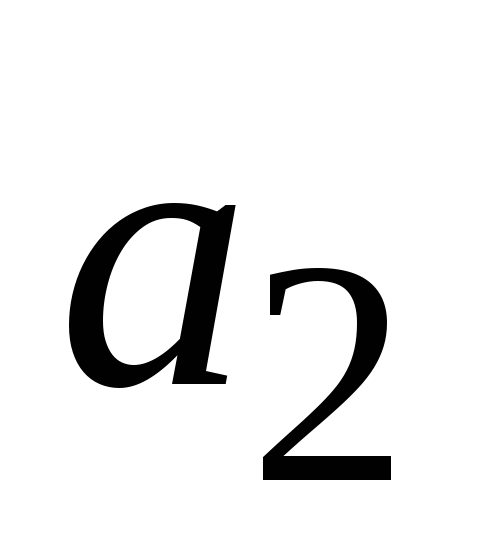
6.2. Законы композиции на множестве.

Множества А, В, С, участвующие в композиции , не обязательно должны быть различными. Если , то говорят, что закон композиции определен на множестве S.

Различают внутренний закон композиции и внешний закон композиции , где Ω и S - различные множества. В случае внутреннего закона говорят, что множество образует группоид относительно операции ┬. В случае внешнего закона композиции элементы называют операторами, а Ω - множеством операторов на множестве S.

Примерами внутреннего закона композиции являются сложение и умножение на множестве действительных чисел, а также геометрическое суммирование векторов на плоскости или в пространстве. Умножение вектора на скаляр может служить примером внешнего закона композиции на множестве векторов, причем операторами являются скаляры - элементы множества действительных чисел.