К курсовой работе по дисциплине Прикладная механика, оКиП

2043.400506.000 Пз

Группа ИДМ-212	Фамилия И.О.	Подпись	Дата	Оценка
Студент
Консультант
Принял

Уфа 2010г.Введение

Редуктором называют механизм, состоящий из зубчатых передач, выполненный в виде отдельного агрегата и служащий для передачи вращения от вала двигателя к валу рабочей машины.

Назначение редуктора – понижение угловой скорости и соответственно повышение вращающего момента ведомого вала по сравнению с ведущим.

Редуктор состоит из корпуса, в котором помещают элементы передачи – зубчатые колёса, валы, подшипники и т.д. В отдельных случаях в корпусе редуктора размещают так же устройства для смазывания зацеплений и подшипников или устройства для охлаждения.

Редуктор проектируют либо для привода определённой машины, либо по заданной нагрузке (моменту на выходном валу) и передаточному числу без указания конкретного назначения.

Редукторы классифицируют по основным признакам: типу передачи (зубчатые, червячные или зубчато-червячные), числу ступеней (одноступенчатые, двухступенчатые и т.д.), типу зубчатых колёс (цилиндрические, конические, коническо-цилиндрические и т.д.), относительному расположению валов редуктора в пространстве (горизонтальные, вертикальные), особенностям кинематической схемы (развёрнутая, соосная, с развёрнутой ступенью и т.д.).

В данном случае редуктор представляет собой прямозубую передачу. Редуктор является одноступенчатым, установлен с горизонтальным расположением валов.

Выбор электродвигателя. Определение основных кинематических и энергетических параметров редуктора

Определение КПД привода. Общий КПД привода определяем по формуле:

где  - общий КПД привода;

_п1,2 – потери на трение в подшипниках качения;

_м – КПД муфты;

_з – КПД зубчатой передачи 1.

Численные значения КПД определяем по таблице, приведенной в 2: _п1,2 = 0,9925;

_м = 0,985;

_з = 0,965.

Подставив численные значения в формулу получим:

Определение требуемой мощности привода. Требуемая мощность привода определяется по формуле:

где Р - требуемая мощность привода, кВт;

n_вых – частота вращения выходного вала, об/мин 1.

Определение требуемой мощности электродвигателя. Требуемая мощность на валу электродвигателя определяется по формуле:

где Р_р – мощность на валу электродвигателя, кВт;

Р – номинальная мощность на ведомом валу привода, кВт;

 - общий КПД привода 3.

Подставив численные значения в формулу получим:

По каталогу, приведенному в 2, определяем мощность двигателя Р_ном=7,5 кВт.

Определение частоты вращения вала электродвигателя. Требуемая частота вращения вала определяется по формуле:

где n₁ – ребуемая частота вращения вала, об/мин;

n₂ – частота вращения выходного вала, об/мин 1.

Подставив численные значения в формулу (1.4) получим:

Выбор электродвигателя. Согласно рассчитанным данным выбираем по каталогу двигатель типа 132S4/1440, асинхронная частота вращения 1440 об/мин1.

Определение передаточного числа редуктора. Общее передаточное число привода определяем по формуле:

где u - общее передаточное число привода;

n₁ - частота вращения вала электродвигателя, об/мин;

n₂ - частота вращения выходного вала, об/мин.

Подставив численные значения в формулу получим:

_{Примем U=4.5}

Расчет закрытой передачи

Выбор материала зубчатых колес. Основными условиями для выбора материалов и термообработки колес являются:

1) критерии работоспособности, условия нагружения и назначение машин. Наиболее типовым критерием работоспособности зубчатых колес является контактная прочность рабочих поверхностей зубьев. Допускаемые контактные напряжения в зубьях пропорциональны твердости материалов, а допускаемая нагрузка передач по контактной выносливости пропорциональна квадрату твердости. Износостойкость и противозадирные свойства возрастают с увеличением твердости поверхностей зубьев, поэтому целесообразно широкое использование зубчатых колес с высокой поверхностной твердостью зубьев;

2) условие равнопрочности зубьев шестерни и колеса. Для обеспечения одинаковой контактной выносливости зубьев шестерни и колеса рекомендуется назначать такое сочетание материалов колес, чтобы твердость поверхности зубьев шестерни превышала твердость зубьев колеса на 25…70 НВ;

3) при твердости рабочих поверхностей зубьев обоих колес НВ  350 передачи являются плохо прирабатывающимися, при твердости НВ ≤ 350 хотя бы одного из колес возможна приработка зубьев. В связи с этим для колес с твердостью НВ  350 назначаются марки стали, подвергаемые закалке с нагревом ТВЧ, цементации, азотированию, а при НВ ≤ 350 – стали, подвергаемые улучшению, редко – нормализации;

4) технология изготовления зубчатых колес;

5) конструкция, размеры, точность зубчатых колес, методы обработки зубьев и виды термообработки 3.

Для колеса и шестерни выбираем материал – сталь 40Х, вид термообработки – улучшение.

Твердость поверхности колеса 235…262 НВ, шестерни – 269…302НВ1.

Определение допускаемых напряжений.

Допускаемое контактное напряжение рассчитывают для каждого зубчатого колеса передачи по формуле:

где _Н1,2 - допускаемое контактное напряжение, МПа;

_Нlim1,2 – предел выносливости материала, МПа;

S_Н1,2 – коэффициент безопасности;

Z_N1,2 – коэффициент долговечности 1.

Предел выносливости _Нlim1,2 назначаем по эмпирическим зависимостям в зависимости от вида термообработки:

где - среднее значение твердости материала.

Подставив численные значения в формулу получим:

Коэффициент безопасности назначаем в зависимости от вида термообработки (в данной работе – улучшение) и принимаем S_Н1,2 = 1,1 1.

Коэффициент долговечности Z_N1,2 определяем по формуле:

где N_HG1,2 – базовое число циклов;

N_НЕ1,2 – эквивалентное число циклов до разрушения при расчетном контактном напряжении (при переменных режимах нагрузки) 5.

Эквивалентное число циклов определяем по формуле:

где _Н – коэффициент эквивалентности;

N_Н1,2 – циклическая долговечность.

Коэффициент эквивалентности определяем в зависимости от режима работы и вида термообработке по таблице, приведенной в 1: _Н = 0,125.

Циклическую долговечность определяем по формуле:

где с – число зацеплений зуба за один оборот (для проектируемого редуктора с = 1);

n_1,2 – частота вращения того зубчатого колеса, по материалу которого определяют допускаемые напряжения, об/мин;

t – время работы передачи (ресурс), ч; t = L_h 1.

Подставив численные значения в формулу получим:

Полученные данные подставляем в формулу :

Базовое число циклов N_HG перемены напряжений рассчитывают по следующим эмпирическим зависимостям:

Подставив численные значения в формулу получим:

Полученные данные подставляем в формулу и определяем коэффициент долговечности Z_N1,2:

принимаемZ_N1 = 1;

принимаемZ_N2 = 1;

По вычисленным данным определяем допускаемое контактное напряжение по формуле :

Из двух значений рассчитанного допускаемого контактного напряжения в дальнейшем для прямозубых конических передач, у которых зубья шестерни значительно тверже зубьев колеса за расчетное принимаем _Н_min – меньшее из значений _Н1] и _Н2]. 1.

Допускаемые напряжения изгиба _F_1,2 вычисляются по формуле:

где _Flim – предел выносливости зубьев по напряжениям изгиба, МПа;

S_F – коэффициент безопасности;

Y_А – коэффициент, учитывающий влияние двустороннего приложения нагрузки;

Y_N – коэффициент долговечности 1.

Коэффициент безопасности принимаем S_F = 1,7, [5] при односторонней нагрузке Y_А = 1 1.

Коэффициент долговечности Y_N определяем по формуле (при НВ ≤ 350):

где N_FG – базовое число циклов;

N_FE – эквивалентное число циклов.

Для всех сталей рекомендуют принимать N_FG = 410⁶ 1.

При переменных режимах нагрузки N_FE определяют по формуле:

Коэффициент эквивалентности принимаем по таблице, приведенной в 1: _F = 0,038 1.

Подставив численные значения в формулу получим:

По полученным данным определяем коэффициент долговечности Y_N по формуле :

принимаемY_N1 = 1;

принимаемY_N2 = 1;

Предел выносливости _Flim1,2 назначаем по эмпирическим зависимостям в зависимости от вида термообработки:

где - среднее значение твердости материала1.

По полученным данным определяем допускаемые напряжения изгиба по формуле :

Расчет закрытой конической зубчатой передачи.

Проектный расчет. Основной габаритный размер передачи - делительный диаметр колеса по внешнему торцу - рассчитывают по формуле:

,

где Е_пр – приведенный модуль упругости, МПа;

Т₂ - вращающий момент на колесе передачи, Нмм;

К_Н - коэффициент неравномерности нагрузки по длине контакта;

u_р – расчетное передаточное число конической передачи;

_Н - допускаемое контактное напряжение, МПа;

- коэффициент ширины зубчатого венца относительно внешнего конусного расстояния.

Е_пр принимают для стальных колёс Е_пр=Е_стали=2,1·10⁵ МПа;

Т₂ – рассчитывают по формуле:

;

- коэффициент неравномерности распределения нагрузки по длине зуба, определяют по графикам на рис.1.1.

Здесь . Рекомендуют принять . Наиболее распространено в редукторостроении значениепредыдущее выражение для определения делительного диаметра по внешнему торцу колеса принимает вид

Геометрический расчёт. Определяют диаметр шестерни по внешнему торцу.

Число зубьев шестерни назначают по рекомендациям, представленным на рис. 2.6.

По значению определяют число зубьев шестерни:

Вычисленное значение z₁округляют до целого числа.

Рис.2.6

Определяют число зубьев колеса .

Вычисленное значение z₂ округляют до целого числа.

После необходимо уточнить:

- передаточное число передачи =135/30=4,5,

- угол делительного конуса колеса,

- угол делительного конуса шестерни,

- внешний окружной модуль .

Рекомендуется округлить т_е до стандартного значеният_е=2.

После этого уточняют величины диаметров.

d =m=60

d =mz₂=270

Рассчитывают величину внешнего конусного расстояния передачи

R_e =

Рабочая ширина зубчатого венца колеса

Полученное значение b_w округляют до ближайшего из ряда нормальных линейных размеров

.

Определяют расчётный модуль зацепления в среднем сечении зуба

При этом найденное значение т_т не округляют!

Рассчитывают внешнюю высоту головки зуба h=m=2

Внешнюю высоту ножки зуба определяют как h = 1,2m.=2,4

Внешний диаметр вершин зубьев колёс рассчитывают по формуле

64

271

Угол ножки зуба рассчитывают по формуле:

Проверочный расчёт. При расчёте на выносливость зубьев колёс по контактным напряжениям проверяют выполнение условия

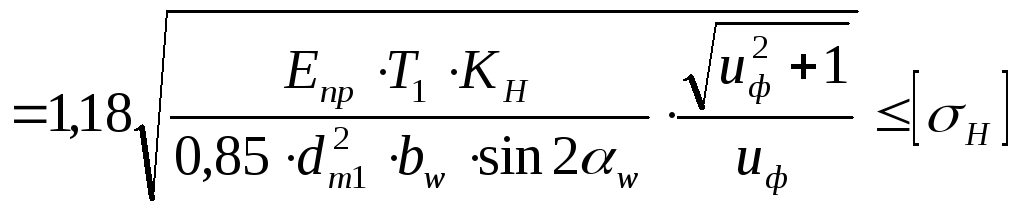
где Е- приведённый модуль упругости, для стальных колёсЕ⁼E= 2,1*10МПа;

T - вращающий момент на шестерне, Н·мм,

где - кпд передачи

К_н - коэффициент расчётной нагрузки,К_Н =К·K_HV; коэффициент концентрации нагрузкиКнайден ранее по графикам рис.2.5.

К-коэффициент динамической нагрузки, находят по табл. 2.7 с понижением на одну степень точности против фактической, назначенной по окружной скоростиV=в соответствии с рекомендация (табл.2.6);

d_m1 - делительный диаметр шестерни в среднем сечении зуба,

^;мм

м/с

К=1,05

- угол зацепления, .

Далее проверяют зубья колёс на выносливость по напряжениям и на изгиб по формулам [1]:

и

где F_t - окружное усилие в зацеплении, Н,F = 2T/d=1,75;

К-коэффициент расчётной нагрузки,K_F=K. ЗдесьK =1+1,5·(K-1), аK определяют по табл. 2.7 с понижением точности на одну степень против фактической.

K =1+1,5·(1,05-1)=1,075

Y- коэффициент формы зуба соответственно шестерни и колеса, находят по табл. 2.9 в зависимости от эквивалентного числа зубьев колёс