14.4. Выборочное уравнение линейной регрессии. Метод наименьших квадратов
При проведении современных клинических исследований обычно нет недостатка в информации: каждому пациенту соответствует целое множество различных клинических показателей и данных.
В них могут быть завуалированы некоторые соотношения, основные черты которых и позволяют выявлять методы регрессионного анализа.
При этом задача регрессионного анализа состоит в подборе упрощенной аппроксимации этой связи с помощью математической модели.
Регрессионный анализ имеет в своем распоряжении специальные процедуры проверки, является ли выбранная математическая модель адекватной для описания имеющихся данных.
Чаще всего регрессионный анализ используется для прогноза, то есть предсказания значений ряда зависимых переменных по известным значениям других переменных.
Выше указывалось, что результаты наблюдений, приведенные в двумерной выборке:
|
xi |
x1 |
x2 |
x3 |
x4 |
x5 |
|
yi |
y1 |
y2 |
y3 |
y4 |
y5 |
можно представить в виде корреляционного поля точек (рис. 14.3), где каждая точка соответствует отдельным значениям х и у.
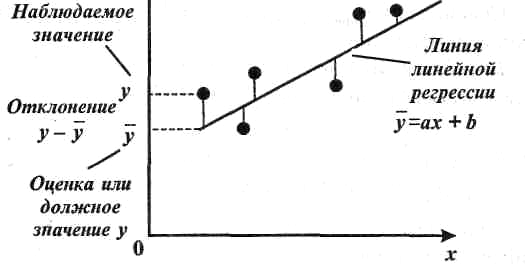
Рис. 14.3. Метод наименьших квадратов
В результате получается диаграмма рассеяния, позволяющая судить о форме и тесноте связи между варьирующими признаками. Довольно часто эта связь может быть аппроксимирована прямой линией (рис. 14.3).
Регрессия - это функция, позволяющая по величине одного признака X находить среднее ожидаемое (должное) значение другого признака Y, корреляционно связанного с X.
В линейной математической модели уравнение линейной регрессии имеет вид:
,
где а и b - параметры линейной регрессии;
а - это коэффициент регрессии, показывающий, насколько в среднем величина одного признака Y изменяется при изменении на единицу меры другого признака X, корреляционно связанного с Y. Чем больше a - угловой коэффициент прямой а= tg α, тем круче прямая, то есть быстрее изменяется Y.
b
- свободный
член в уравнении, определяет
;
при x
= 0.
-
это предсказанное (должное) значение
Y
для данного
х при
определенных значениях регрессионных
параметров.
Параметры линейной регрессии определяют методом наименьших квадратов - это способ подбора параметров регрессионной модели, согласно которому сумма квадратов отклонений вариант от линии регрессии должна быть минимальна:
Это эффективный метод, позволяющий уменьшить влияние ошибок измерений.
Теперь
определяют должные величины
,
наносят эти
точки и соединяют их прямой линией.
Достоинство корреляционно-регрессионного анализа - наглядное представление о форме и тесноте связи. Регрессия выражает корреляционную зависимость в виде функционального отношения и дает более полную информацию.
Была исследована зависимость между ростом (X) и массой (Y), у 200 животных и рост, и масса подчиняются нормальному закону распределения. На рис. 3а видно, что эта зависимость линейная: чем больше рост, тем больше масса.
Из этой совокупности выберем выборку объема п = 10 (рис. 13.4б). Сохранилась ли эта зависимость массы от роста? На рис. 13.4б изображены 4 прямые, аппроксимирующие эту зависимость. Какую прямую можно считать наилучшей?
Рис 14.4. Зависимость между ростом (X) и массой (Y) у животных
Ответ: Да, сохранилась. Прямая I - не годится - все точки оказались по одну сторону от нее. Прямая II – слишком круто устремляется вверх.
Лучше прямые III и IV, а из них лучше та, которая ближе ко всем точкам выборки, то есть относительно которой разброс точек минимален.
Согласно
методу наименьших квадратов лучше
представляет зависимость
от х
прямая IV.
По данным примера № 2:
|
Xi |
31 |
32 |
33 |
34 |
35 |
35 |
40 |
41 |
42 |
46 |
|
Yi |
7,8 |
8,3 |
7,6 |
9,1 |
9,6 |
9,8 |
11,8 |
12,1 |
14,7 |
13,0 |
Рассчитать
параметры уравнения регрессии
по формулам:
Решение:
Именно это уравнение задает прямую IV в задаче № 6.
В примере № 2 был рассчитан коэффициент корреляции между ростом (X) и массой (Y) некоторых животных, а в примере № 7 было составлено уравнение линейной регрессии.
Как вы думаете, если поменять х и у, то изменится ли уравнение регрессии и коэффициент корреляции?
Ответ: r - останется прежним, r = 0,925 - он симметричен, а уравнение регрессии получится другим. Получается, что связь роста с массой одна, а роста с массой - другая. Регрессионный анализ асимметричен - это мешает его использовать для характеристики силы связи.
Провести корреляционно-регрессионный анализ. Построить корреляционное поле точек, проверить значимость (α ≤ 0,05) коэффициента корреляции между переменными X и Y и построить линию регрессии.
Изучали зависимость между содержанием вещества X в ткани С и приростом концентрации вещества Y в крови у пациентов, получавших препарат А.
Результаты наблюдений приведены в виде двумерной выборки объема 10:
|
xi |
1,15 |
1,9 |
3 |
5,34 |
5,4 |
7,7 |
7,9 |
9,03 |
9,37 |
10,18 |
|
yi |
0,99 |
0,98 |
2,6 |
5,92 |
4,33 |
7,68 |
9,8 |
9,47 |
10,64 |
12,9 |
Результаты расчета на компьютере:
r
= 0,94;
tнабл
= 6,17;
= 0,579 + 1,1354 ∙
х
Решение:
Н0: rген = 0; Н1: rген ≠ 0.
Найдем из таблицы tкрит = 2,31; α ≤ 0,05;
f = 10 - 2 = 8.
Сравним: tнабл > tкрит(α, f); 6,17 > 2,31.
Отвергается H0 принимается H1.
Имеется очень сильная линейная корреляционная связь между признаками r = 0,94 (α ≥ 0,05).
Построим корреляционное поле точек (рис. 13.5).
Рис. 13.5. График решения задачи 9
Рассчитаем должные величины:
при
x
= 0,
= -0,576;
при
х = 1,
= 0,556.
Нанесем линию регрессии на график.