8.2. Основные методы интегрирования

8.2.1. Формула Ньютона-Лейбница

Для вычисления определенного интеграла от непрерывной на отрезке [a;b] функции f(x) в том случае, когда может быть найдена ее первообразная F(x) служит формула Ньютона-Лейбница:

,

т.е. определенный интеграл равен разности значений любой первообразной при верхнем и нижнем пределах интегрирования.

При интегрировании четных и нечетных функций в симметричных пределах интегрирования используют формулу

Пример. Вычислить определенные интегралы.

1).

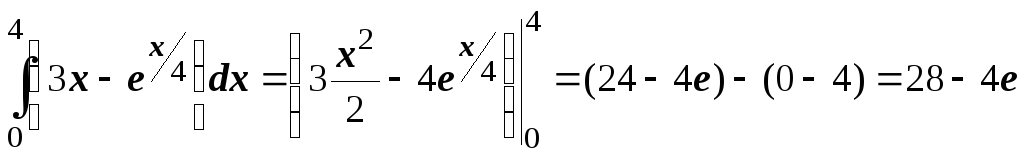2)

8.2.2. Метод подстановки

При вычислении определенного интеграла методом замены переменной (метод подстановки) данный интеграл преобразуется с помощью подстановки t=(x) или x=(t) в определенный интеграл относительно новой переменной интегрирования t. При этом старые пределы интегрирования a, b заменяются новыми переделами интегрирования  и  соответственно, которые находятся из исходной подстановки.

Из первой подстановки новые пределы интегрирования вычисляются непосредственно: =(a), =(b). Из второй подстановки новые пределы интегрирования находятся путем решения уравнений ()=a, ()=b относительно  и .

Таким образом, имеем

Здесь предполагается, что функции (t) и ΄(t) непрерывны на отрезке [; ], а функция f((t)) определена и непрерывна на отрезке  t  .

Пример. Вычислим методом подстановки интеграл .

Решение. Введем новую переменную интегрирования с помощью подстановки t=2x–1. Дифференцируя, получим dt=2dx, откуда dx=dt/2. Находим новые пределы интегрирования: подставляем в соотношение t=2x–1 значения x=2, х=3. Тогда получим α=3, β=5. Следовательно,

.

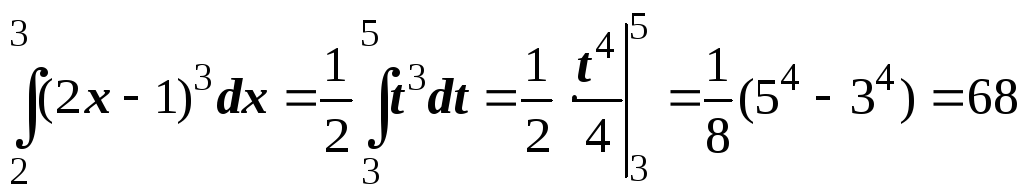В дальнейшем при решении методом подстановки будем использовать форму записи как в неопределенном интеграле, используя вертикальные скобки.

8.2.3. Интегрирование по частям

Если функции u=u(x) и v=v(x) имеют непрерывные производные на отрезке [a; b], то для вычисления определенного интеграла используют формулу , которая называется формулой интегрирования по частям для определенного интеграла.

Пример. Вычислить интеграл .

Решение. Положим Тогда По формуле интегрирования по частям имеем

.

8.3. Примеры

1. Используя формулу Ньютона-Лейбница, найти интегралы:

1. ;

2. ;

3. ;

4. .

Решение.

1. Для нахождения первообразной проведем преобразования, чтобы получить табличный интеграл (в подкоренном выражении выделим полный квадрат):

2. 

.

3. 

4. .

2. Вычислить интегралы методом подстановки:

1. ;

2. ;

3. ;

4. .

Решение.

1. 

2. 

3. 

4. 

.

3. Вычислить интегралы, применяя формулу интегрирования по частям:

1. ;

2. .

Решение.

1. 

2.