
- •2010 Реферат
- •Привод ленточного фильтра, вал быстроходный, вал промежуточный, вал тихоходный, редуктор.
- •Введение
- •1.2 Определение требуемой частоты вала электродвигателя
- •1.3 Выбор электродвигателя
- •1.5 Угловые скорости
- •1.6 Вращающие моменты на валах
- •3.1 Расчет тихоходной передачи
- •4.1 Предварительный расчет валов
- •4.2 Построение эпюр изгибающих и крутящих моментов
- •4.3 Расчет валов на усталостную прочностью
- •7 Выбор системы смазки и смазочных материалов
- •8 Расчет муфты
4.3 Расчет валов на усталостную прочностью
Материал валов – сталь марки 45, механические характеристики которой приведены в таблице 3.
Таблица 3 – Механические свойства стали 45
|
Марка стали |
Твердость НВ, не ниже |
Механические характеристики | |
|
σВ, МПа |
σТ, МПа | ||
|
Сталь 45 |
240 |
800 |
550 |
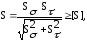 (4.3.1)
(4.3.1)
где
[S]
= 1,5 – допускаемый коэффициент запаса
на усталостную прочность;
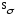 и
и
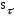 – коэффициенты запаса на усталость по
нормальным и касательным напряжениям:
– коэффициенты запаса на усталость по
нормальным и касательным напряжениям:
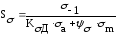 (4.3.2)
(4.3.2)
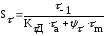 (4.3.3)
(4.3.3)
где σ-1 и τ-1 – пределы выносливости материала детали соответственно при симметричном изгибе и кручении, МПа;
КσД и КτД – коэффициенты концентрации напряжений, учитывающие влияние основных факторов на сопротивление усталости соответственно при изгибе и кручении,;
Ψσ и Ψτ - коэффициенты, характеризующие чувствительность материала к асимметрии цикла напряжений;
σа и τа – амплитуды напряжений цикла, МПа;
σm и τm – средние напряжения цикла, МПа.
Пределы выносливости вала в рассматриваемом сечении:
σ-1 = 0,43 . σВ (4.3.4)
τ-1 = 0,6 . σ-1 (4.3.5)
Напряжения в опасных сечениях:
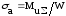 (4.3.6)
(4.3.6)
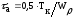 (4.3.7)
(4.3.7)
где

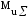 – результирующий изгибающий момент в
опасном сечении;
– результирующий изгибающий момент в
опасном сечении;
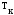 –крутящий
момент;
–крутящий
момент;
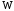 и
и
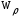 –
осевой и полярный моменты сопротивления
сечения вала.
–
осевой и полярный моменты сопротивления
сечения вала.
Значения КσД и КτД находят по зависимостям:
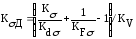 (4.3.8)
(4.3.8)
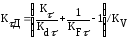 (4.3.9)
(4.3.9)
где Кσ и Кτ – эффективные коэффициенты концентрации напряжений;
Кdσ и Кdτ – коэффициенты, учитывающие размеры вала;
КFσ и КFτ – коэффициенты, учитывающие качество обработки поверхности;
КV– коэффициент, учитывающий вид поверхностного упрочнения.

Определение коэффициента запаса прочности для входного вала
Наиболее опасным сечением является сечение, в котором возникает наибольший изгибающий момент.
Результирующий изгибающий момент:
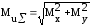 (4.3.10)
(4.3.10)
подставляя данные в формулу (4.3.10), получается:
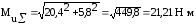
Крутящий момент Tк = 13,14Н·м.
Осевой момент сопротивления сечения:
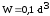 (4.3.11)
(4.3.11)
подставляя данные в формулу (4.3.11) получается:
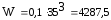 мм
мм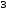
Полярный момент сопротивления сечения:
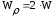 (4.3.12)
(4.3.12)
подставляя данные в формулу (4.3.12) получается:
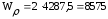 мм
мм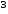
Напряжения в опасных сечениях:
подставляя данные в формулу (4.3.6) получается:
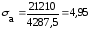 МПа
МПа
подставляя данные в формулу (4.3.7) получается:
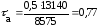 МПа
МПа
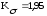 ;
;
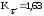 ;
;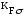 =
0,84;
=
0,84;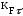 =0,9;
=0,9;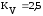
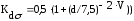 (4.3.13)
(4.3.13)
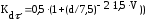 (4.3.14)
(4.3.14)
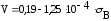 (4.3.15)
(4.3.15)
подставляя данные в формулу (4.3.15) получается:
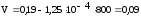
подставляя
данные в формулу (4.3.13) получается:
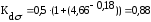
подставляя данные в формулу (4.3.14) получается:
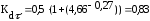
Тогда коэффициенты концентрации напряжений для данного сечения вала:
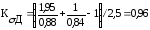
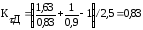
Пределы выносливости вала в рассматриваемом сечении:
подставляя данные в формулу (4.3.4) получается:
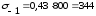 МПа
МПа
подставляя данные в формулу (4.3.5) получается:
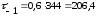 МПа.
МПа.
Коэффициенты запаса по нормальным и касательным напряжениям:
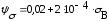 (4.3.16)
(4.3.16)
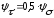 (4.3.17)
(4.3.17)
подставляя данные в формулу (4.3.16) получается:
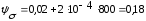
подставляя данные в формулу (4.3.17) получается:
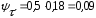
подставляя данные в формулу (4.3.2) получается:
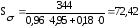
подставляя данные в формулу (4.3.3) получается:
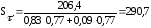
Тогда расчетный коэффициент запаса прочности:
подставляя данные в формулу (4.3.1) получается:
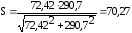
Условие усталостной прочности выполняется.
б) Определение коэффициента запаса прочности для промежуточного вала
Результирующий изгибающий момент:
подставляя данные в формулу (4.3.10), получается:
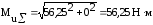
Крутящий момент Tк = 50,99 Н·м.
Осевой момент сопротивления сечения:
подставляя данные в формулу (4.3.11) получается:
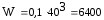 мм
мм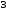
Полярный момент сопротивления сечения:
подставляя данные в формулу (4.3.12) получается:
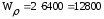 мм
мм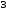
Напряжения в опасных сечениях:
подставляя данные в формулу (4.3.6) получается:
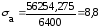 МПа
МПа
подставляя данные в формулу (4.3.7) получается:
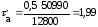 МПа
МПа
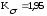 ;
;
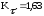 ;
;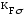 =
0,84;
=
0,84;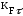 =0,9;
=0,9;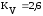
подставляя данные в формулу (4.3.15) получается:
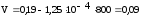
подставляя
данные в формулу (4.3.13) получается:
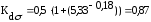
подставляя данные в формулу (4.3.14) получается:
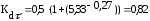
Коэффициенты концентрации напряжений для данного сечения вала:
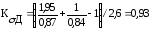
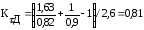
Пределы выносливости вала в рассматриваемом сечении:
подставляя данные в формулу (4.3.4) получается:
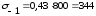 МПа
МПа
подставляя данные в формулу (4.3.5) получается:
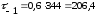 МПа.
МПа.
Коэффициенты запаса по нормальным и касательным напряжениям:
подставляя данные в формулу (4.3.16) получается:
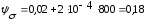
подставляя данные в формулу (4.3.17) получается:
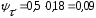
подставляя данные в формулу (4.3.2) получается:
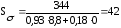
подставляя данные в формулу (4.3.3) получается:
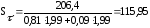

Тогда расчетный коэффициент запаса прочности:
подставляя данные в формулу (4.3.1) получается:
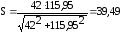
Условие усталостной прочности выполняется.
в) Определение коэффициента запаса прочности для выходного вала
Результирующий изгибающий момент:
подставляя данные в формулу (4.3.10), получается:
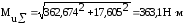
Крутящий момент Tк = 175,73 Н·м.
Осевой момент сопротивления сечения:
подставляя данные в формулу (4.3.11) получается:
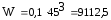 мм
мм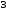
Полярный момент сопротивления сечения:
подставляя данные в формулу (4.3.12) получается:
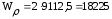 мм
мм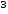
Напряжения в опасных сечениях:
подставляя данные в формулу (4.3.6) получается:
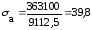 МПа
МПа
подставляя данные в формулу (4.3.7) получается:
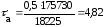 МПа
МПа
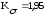 ;
;
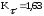 ;
;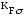 =
0,84;
=
0,84;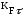 =0,9;
=0,9;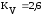
подставляя данные в формулу (4.3.15) получается:
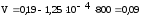
подставляя
данные в формулу (4.3.13) получается:
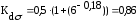
подставляя данные в формулу (4.3.14) получается:
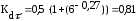
Коэффициенты концентрации напряжений для данного сечения вала:
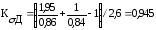
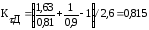
Пределы выносливости вала в рассматриваемом сечении:
подставляя данные в формулу (4.3.4) получается:
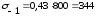 МПа
МПа
подставляя данные в формулу (4.3.5) получается:
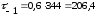 МПа.
МПа.
Коэффициенты запаса по нормальным и касательным напряжениям:
подставляя данные в формулу (4.3.16) получается:
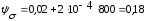
подставляя данные в формулу (4.3.17) получается:
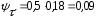
подставляя данные в формулу (4.3.2) получается:
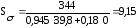
подставляя данные в формулу (4.3.3) получается:
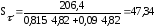

Тогда расчетный коэффициент запаса прочности:
подставляя данные в формулу (4.3.1) получается:
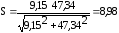
Условие усталостной прочности выполняется.
Расчет подшипников качения

Подшипники качения выполняют функцию опор вращающихся валов.
Входной вал
Задаемся шариковыми радиально-упорными однорядными подшипниками по ГОСТ 831-75 средней серии (46307)
Исходные данные:
d = 35 мм – внутренний диаметр подшипника;
D = 80 мм – наружный диаметр подшипника;
В = 21 мм – ширина подшипника;
r = 2,5 мм – высота фаски;
r1 = 1,2 мм – высота фаски;
Cr = 42,6 кН – динамическая грузоподъёмность;
Cor = 24,7 кН – статическая грузоподъёмность;
Fr1 = 653,55 H; Fr2 = 456,95 H – суммарные реакции в опорах;
Fa = 0 H – осевая нагрузка;
Ft = 725H – окружная нагрузка;
n = 2850 мин-1
α = 120 – номинальный угол контакта
Определение составляющих опорных реакций подшипников
Определение радиальных опорных реакций подшипников:
a = 0,5 . [В + 0,5(d + Д) . tg α] (5.1)
Подставляя данные в формулу (5.1) получаем
а = 0,5 . [21 + (35+80) . 0,21]= 22,57
Определение осевых опорных реакций подшипников:
Сила Famin - сила, которая должна действовать на радиально-упорный подшипник при заданной радиальной силе Fr
Famin = е΄ . Fr , (5.2)
где е΄ - коэффициент минимальной осевой нагрузки
Подставляя данные в формулу (5.2) получаем:
Famin1 = 0,35. 653,55 = 228,74 Н
Famin2 = 0,33 . 456,95 = 150,79 Н
Fa1 = Famin1;
Fa1 = 228,74 H
Fa2 = Fa+ Fa1
Fa2 = 0 + 228,74 = 228,74 H
Расчеты проводим по второму подшипнику. Направление Fa – слева направо.
Расчет подшипников на долговечность
Lh
= a1
.
a23
.
(С/Р)m
.
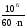
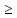 [Lh]
(5.3)
[Lh]
(5.3)
где Lh – расчетная долговечность подшипника, ч;
[Lh] – требуемая долговечность подшипника, ч;
n – частота вращения вала (корпуса), мин -1;
С – динамическая грузоподъемность подшипника, Н;
Р – эквивалентная динамическая нагрузка, Н;
m
– показатель степени, m
= 3;
a1 – коэффициент, учитывающий надежность работы
подшипника, a1=1;
a23 – обобщенный коэффициент совместного влияния
качества металла и условий эксплуатации, a23=0,75
Эквивалентная динамическая нагрузка Р для радиальных и радиально-упорных шарико– и роликоподшипников есть такая условная постоянная стационарная радиальная сила Рr, которая при приложении её к подшипнику с вращающимся внутренним кольцом и с неподвижным наружным обеспечивает такую же долговечность, какую подшипник имеет при действительных условиях нагружения и вращения.
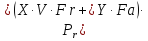 Kσ
Kσ
 Kt
(5.4)
Kt
(5.4)
где Fr и Fa – радиальная и осевая силы;
X, Y – коэффициент радиальной и осевой силы;
V – коэффициент вращения, зависящий от того, какое кольцо
подшипника вращается относительно внешней нагрузки,
V = 1;
Kσ – коэффициент безопасности, учитывающий характер
нагрузки;
Kt - температурный коэффициент, Kt = 1.
CΣ = 1,625 . C (5.5)
CΣ = 1,625 . 42600 = 69225 Н
Подставляя данные в формулу (5.4) получаем:
Pr = (0,45 . 456,95 + 1,81. 228,74) .2,2 . 1 = 1363,23 H
Подставляя данные в формулу (5.3) получаем
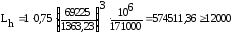 -
верно
-
верно
Подшипник проходит.
Расчет подшипников на статическую грузоподъемность

Fr ≤ Cor; Cor = 24700 H
Por = X0 . Fr + Y0 . Fa (5.6)
Подставляя данные в формулу (5.6) получаем
Por = 0,5 . 456,95 + 0,47 . 228,74 = 335,98 ≤ 24700 – верно
Подшипник проходит.
Промежуточный вал
Задаемся шариковыми радиально-упорными однорядными подшипниками по ГОСТ 831-75 средней серии (46308)
Исходные данные:
d = 40 мм – внутренний диаметр подшипника;
D = 90 мм – наружный диаметр подшипника;
В = 23 мм – ширина подшипника;
r = 2,5 мм – высота фаски;
r1 = 1,2 мм – высота фаски;
Cr = 50,0 кН – динамическая грузоподъёмность;
Cor = 30,1кН – статическая грузоподъёмность;
Fr1 = 1153,07 H; Fr2 = 1510,43 H – суммарные реакции в опорах;
Fa = 0 H – осевая нагрузка;
n = 712,5 мин-1
α = 120 – номинальный угол контакта
Определение составляющих опорных реакций подшипников
Определение радиальных опорных реакций подшипников:
Подставляя данные в формулу (5.1), получаем
а = 0,5 . [23 + (40+90) . 0,21] = 25,15
Определение осевых опорных реакций подшипников:
Сила Famin - сила, которая должна действовать на радиально-упорный подшипник при заданной радиальной силе Fr
Подставляя данные в формулу (5.2) получаем:
Famin1 = 0,36. 1153,07 = 415,1 Н
Famin2 = 0,37 . 1510,43 = 558,86 Н
Fa2 = Famin2;
Fa2 = 558,86 Н
Fa1 = Fa2 - Fa
Fa1 = 558,86 – 0 = 558,86 H
Расчеты проводим по второму подшипнику.
Расчет подшипников на долговечность
CΣ = 1,625 . C
CΣ = 1,625 . 50000 = 81250 Н
Подставляя данные в формулу (5.4) получаем:
Pr = (0,45 . 1510,43 + 1,7. 558,86) .2,2 . 1 = 3585,45 H
Подставляя данные в формулу (5.3) получаем
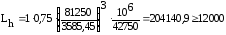 -
верно
-
верно
Подшипник проходит.
Расчет подшипников на статическую грузоподъемность

Fr ≤ Cor; Cor = 30100 H
Por = X0 . Fr + Y0 . Fa
Подставляя данные в формулу (5.6) получаем
Por = 0,5 . 1510,43 + 0,47 . 558,86 = 1017,86 ≤ 30100 – верно
Подшипник проходит.
Выходной вал
Задаемся шариковыми радиально-упорными однорядными подшипниками по ГОСТ 831-75 средней серии (46309)
Исходные данные:
d = 45 мм – внутренний диаметр подшипника;
D = 100 мм – наружный диаметр подшипника;
В = 24 мм – ширина подшипника;
r = 2,5 мм – высота фаски;
r1 = 1,2 мм – высота фаски;
Cr = 61,4 кН – динамическая грузоподъёмность;
Cor = 37 кН – статическая грузоподъёмность;
Fr1 = 3792,9 H; Fr2 = 6257,55 H – суммарные реакции в опорах;
Fa = 0 H – осевая нагрузка;
n = 200,7 мин-1
α = 120 – номинальный угол контакта
Определение составляющих опорных реакций подшипников
Определение радиальных опорных реакций подшипников:
Подставляя данные в формулу (5.1), получаем
а = 0,5 . [24 + (45+100) . 0,21] = 27,225
Определение осевых опорных реакций подшипников:
Сила Famin - сила, которая должна действовать на радиально-упорный подшипник при заданной радиальной силе Fr
Подставляя данные в формулу (5.2) получаем:
Famin1 = 0,42. 3792,9 = 1593 Н
Famin2 = 0,45 . 6257,55 = 2815,9 Н
Fa2 = Famin2;
Fa2 = 2815,9 Н
Fa1 = Fa2 - Fa
Fa1 = 2815,9 – 0 = 2815,9 H
Расчеты проводим по второму подшипнику.
Расчет подшипников на долговечность
CΣ = 1,625 . C
CΣ = 1,625 . 61400 = 99775 Н
Подставляя данные в формулу (5.4) получаем:
Pr = (0,45 . 6257,55 + 1,4. 2815,9) .2,2 . 1 = 14867,86 H
Подставляя данные в формулу (5.3) получаем
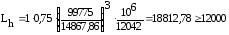 -
верно
-
верно
Подшипник проходит.
Расчет подшипников на статическую грузоподъемность

Fr ≤ Cor; Cor = 30100 H
Por = X0 . Fr + Y0 . Fa (5.6)
Подставляя данные в формулу (5.6) получаем
Por = 0,5 . 6257,55 + 0,47 . 2815,9 = 4452,2 ≤ 37000 – верно
Подшипник проходит.
Таблица 4 – Расчет подшипников
|
Вал |
Обозна-чение |
d, мм |
D, мм |
В, мм |
r, мм |
r1, мм |
Cr, кH |
Cor, кH |
Lh,ч |
Por, Н |
|
Входной |
46307 |
35 |
80 |
21 |
2,5 |
1,2 |
42,6 |
24,7 |
574511,36 |
335,98 |
|
Промежу- точный |
46308 |
40 |
90 |
23 |
2,5 |
1,2 |
50,0 |
30,1 |
204140,9 |
1017,8 |
|
Выходной |
46309 |
45 |
100 |
24 |
2,5 |
1,2 |
61,4 |
37,0 |
18812,78 |
4452,2 |
Расчет шпонок

Предварительный подбор шпонок
Таблица 5 - Предварительный подбор шпонок
|
Диаметр вала d |
Сечение шпонки |
Глубина паза |
Фаска s x 45° | ||
|
Вала t1 |
Втулки t2 | ||||
|
8 x 7 |
4,0 |
3,3 |
0,16 – 0,25 | |
|
12 x 8 |
5,0 |
3,3 |
0,25 – 0,40 | |
|
12 x 8 |
5,0 |
3,3 |
0,25 – 0,40 | |
|
14 x 9 |
5,5 |
3,8 |
0,25 – 0,40 | |
|
12 x 8 |
5,0 |
3,3 |
0,25 – 0,40 | |
Проверочный расчет шпонок
В
качестве материала для шпонок выбираем
Сталь 45. Шпонки проверяем на срез и
смятие рабочих поверхностей.
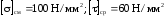
Условия прочности:
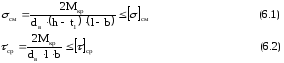
Длина шпонки l:
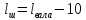 (6.3)
(6.3)
Быстроходный вал:
Первая шпонка:
Установлена
на участке входного вала диаметром
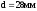 ,
,
крутящий
момент на котором
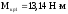
Подставляя данные в формулу (6.3) получаем
lш = 56 - 10=46 мм
Принимаем lш = 45 мм
Подставляя данные в формулу (6.1) получаем
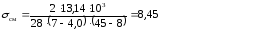
8,45 ≤ 100 – верно
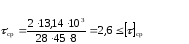

Условиям прочности удовлетворяет
Принимаем
шпонку
Промежуточный вал:
Первая шпонка:
Установлена под колесом быстроходной ступени на участке вала
диаметром
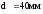
Подставляя данные в формулу (6.3) получаем
lш = 46 – 10 = 36 мм
Принимаем lш = 36 мм
Подставляя данные в формулу (6.1) получаем
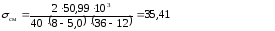
35,41 ≤ 100 – верно
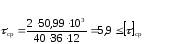
Условиям прочности удовлетворяет
Принимаем
шпонку
Вторая шпонка:
Установлена под шестерней тихоходной ступени на участке вала
Диаметром
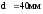 ,
крутящий момент на котором
,
крутящий момент на котором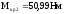 .
.
Подставляя данные в формулу (6.3) получаем
lш = 42 – 10 = 32 мм
Принимаем lш = 32 мм
Подставляя данные в формулу (6.1) получаем
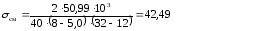
42,49 ≤ 100 – верно
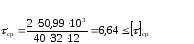
Условиям прочности удовлетворяет
Принимаем
шпонку
Тихоходный
вал:
Первая шпонка:
Установлена под колесом тихоходной ступени на участке вала
диаметром
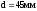 ,
крутящий момент на котором
,
крутящий момент на котором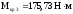 .
.
Подставляя данные в формулу (6.3) получаем
lш = 49 – 10 = 39 мм
Принимаем lш = 40 мм
Подставляя данные в формулу (6.1) получаем
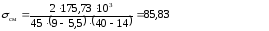
85,83 ≤ 100 – верно
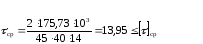
Условиям прочности удовлетворяет
Принимаем
шпонку
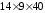
Вторая шпонка:
Установлена
на выходном участке вала диаметром
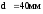 ,
,
крутящий
момент на котором
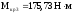 .
.
Подставляя данные в формулу (6.3) получаем
lш = 61,5 – 10 = 51,5 мм
Принимаем lш = 50 мм
Подставляя данные в формулу (6.1) получаем
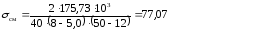
77,07 ≤ 100 – верно
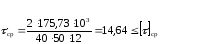
Условиям прочности удовлетворяет
Принимаем
шпонку
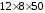
Таблица 6 – Расчет шпонок
|
Диаметр вала d |
Сечение шпонки |
Глубина паза |
Фаска s x 45° |
Длина шпонки, l | |||
|
Вала t1 |
Втулки t2 | ||||||
|
1 |
2 |
3 |
4 |
5 |
6 | ||
|
8 x 7 |
4,0 |
3,3 |
0,16 – 0,25 |
45 | ||
|
Продолжение
таблицы 6 | |||||||
|
1 |
2 |
3 |
4 |
5 |
6 | ||
|
12 x 8 |
5,0 |
3,3 |
0,25 – 0,40 |
36 | ||
|
12 x 8 |
5,0 |
3,3 |
0,25 – 0,40 |
32 | ||
|
14 x 9 |
5,5 |
3,8 |
0,25 – 0,40 |
40 | ||
|
12 x 8 |
5,0 |
3,3 |
0,25 – 0,40 |
50 | ||

