5. Побудова полінома найменшого степеня за відомими коренями.
Оберненою для сімейства задач про існування та визначення коренів поліномів є задача побудови поліному за відомими коренями.
Доведено, що поліноми
-го
степеня, визначені на множені комплексних
чисел
мають точно
коренів. Причому кількість
дійсних коренів буде
або співпадати із загальною кількістю
коренів
або буде
меншим за
на
парне число.
Виходячи з такого факту можна
зробити висновок, що
дійсних коренів належать до поліному
мінімального степеня
.
Спосіб побудови коефіцієнтів такого полінома дає теорема Вієта.
Для коренів
алгебраїчного рівняння
-го
степеня
Справедливі співвідношення:
…………………………….
Наведені формули називаються формулами Вієта.
Якщо поліном заданий на
множині
,
то крім
дійсних коренів поліном
може мати парну кількість
комплексних коренів і
тому загальний степінь полінома буде
більшим за
.
Отже, якщо
задати
дійсних коренів поліному, можна за
формулами Вієта побудувати зведений
(
)
поліном
-го
степеня
Умноживши зведений поліном
на довільну сталу
отримаємо сукупність асоційованих
поліномів найменшого степеня, тобто
поліномів, які можна отримати один з
одного множенням на сталу (поліном
нульового степеня).
Приклад
Відомо, що числа 1, 2, -1, 4, 3 є коренями полінома. Побудувати поліном найменшого степеня, який має такі корені. Побудувати усі асоційовані до нього поліноми.
Розв’язання.
Розглянемо формули Вієта для
п’яти коренів. Маємо
Кількість доданків повинна
дорівнювати кількості сполук з 5 по 2:
.
Вимога виконана.
Кількість доданків повинна
дорівнювати кількості сполук з 5 по 3:
.
Вимога виконана.
Кількість доданків повинна
дорівнювати кількості сполук з 5 по 4:
.
Вимога виконана.
У виведені формули підставимо корені. Отримаємо коефіцієнти зведеного поліному:
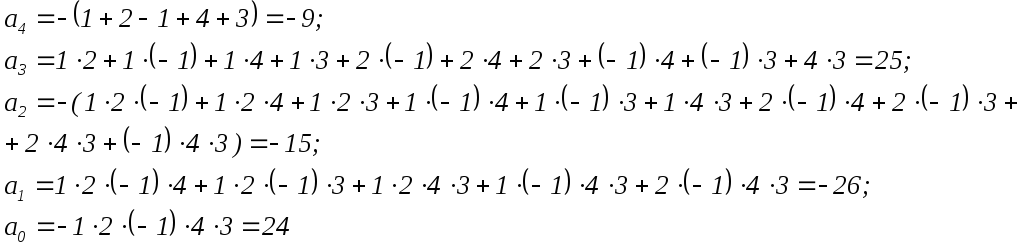
Запишемо зведений поліном:
Перевіримо, чи правильно знайдені коефіцієнти:
корінь
полінома;
корінь
полінома;
Корені -1, 4,3 пропонується студентам перевірити самостійно.
Зведений поліном найменшого степеня побудований правильно. Усі асоційовані поліноми можна записати так:
Індивідуальне завдання 4.
Використовуючи
формули Вієта побудувати зведений
поліном найменшого степеня у множині
за заданими коренями.
Перед
розв’язанням записати загальні формули
для такого поліному. Побудувати усі
поліноми, асоційовані із отриманим
зведеним.
|
Номер варіанту |
|
|
|
|
|
|
1 |
3 |
3 |
3 |
2 |
1 |
|
2 |
2 |
2 |
1 |
1 |
4 |
|
3 |
|
- |
1 |
1 |
1 |
|
4 |
1 |
1 |
1 |
2 |
3 |
|
5 |
3 |
3 |
2 |
2 |
1 |
|
6 |
|
- |
2 |
2 |
-3 |
|
7 |
2 |
2 |
2 |
1 |
4 |
|
8 |
1 |
1 |
3 |
3 |
2 |
|
9 |
2 |
2 |
2 |
1 |
1 |
|
10 |
|
- |
1 |
1 |
1 |
|
11 |
1 |
1 |
1 |
3 |
3 |
|
12 |
3 |
3 |
3 |
1 |
1 |
|
13 |
1 |
1 |
2 |
2 |
3 |
|
14 |
|
- |
2 |
2 |
-2 |
|
15 |
4 |
4 |
4 |
-1 |
-1 |
|
16 |
3 |
3 |
3 |
-2 |
-1 |
|
17 |
|
- |
1 |
1 |
3 |
|
18 |
2 |
2 |
-1 |
-1 |
1 |
|
19 |
-1 |
-1 |
-1 |
2 |
3 |
|
20 |
|
- |
-2 |
-2 |
-2 |
|
21 |
3 |
3 |
-2 |
-2 |
1 |
|
22 |
2 |
2 |
2 |
-1 |
-4 |
|
23 |
|
- |
-1 |
-2 |
-1 |
|
24 |
1 |
1 |
-3 |
-3 |
2 |
|
25 |
|
- |
-1 |
-1 |
-1 |
|
26 |
2 |
2 |
2 |
-1 |
-1 |
|
27 |
-1 |
-1 |
-1 |
3 |
3 |
|
28 |
-1 |
-1 |
2 |
2 |
-3 |
|
29 |
|
- |
-1 |
-1 |
2 |
|
30 |
5 |
3 |
-1 |
-1 |
-1 |
Докладніше дивись отримання кореня n-го степеня з довільного комплексного числа за допомогою значень кореня кубічного з 1. А.Г. Курош Курс высшей алгебры/ М: Наука, 1968, гл.4, §19, стор. 128