
- •Обов’язкова контрольна робота №2 поліноми
- •1 Кубічні рівняння.
- •Індивідуальне завдання 1.
- •2 Обчислення значення полінома та його похідних у точці.
- •1. Розкладання полінома за степенями бінома
- •2. Обчислення похідних полінома в даній точці .
- •Індивідуальне завдання 2.1
- •3 Подільність поліномів. Нсд двох поліномів. Знаходження нсд за алгоритмом Евкліда. Подання нсд через лінійну комбінацію поліномів.
- •Поліном нульового степеня є дільником будь якого полінома степеня .
- •Індивідуальне завдання 2.2
- •4 Розкладання полінома на кратні та незвідні множники.
- •Індивідуальне завдання 3.
- •5. Побудова полінома найменшого степеня за відомими коренями.
- •Індивідуальне завдання 4.
Індивідуальне завдання 2.2
Для поліномів
![]() та
та
![]() з індивідуального завдання 2.1
з індивідуального завдання 2.1
-
Визначити найбільший спільний дільник (НСД);
-
Використовуючи алгоритм Евкліда подати НСД поліномів через лінійну комбінацію цих поліномів. Визначити функції
 та
та
 з лінійного подання. Зробити перевірку
результату.
з лінійного подання. Зробити перевірку
результату.
4 Розкладання полінома на кратні та незвідні множники.
В алгебрі поліномів над довільними полями однією з важливих задач є задача розкладання полінома на незвідні множники. Розв’язання цієї задачі базується на таких твердженнях:
– будь який поліном першого степеня є незвідним;
– якщо поліном
![]() є незвідним, то незвідним буде будь який
поліном
є незвідним, то незвідним буде будь який
поліном
![]() ;
;
– якщо
![]() - довільний поліном, а
- довільний поліном, а
![]() - незвідний, то або
- незвідний, то або
![]() ділиться на
ділиться на
![]() ,
тобто
,
тобто
![]() ,
або поліноми
,
або поліноми
![]() та
та
![]() є взаємно простими, тобто
є взаємно простими, тобто
![]() ;
;
– якщо добуток двох поліномів
![]() та
та
![]() ділиться на незвідний поліном
ділиться на незвідний поліном
![]() ,
то обов’язково або
,
то обов’язково або
![]() або
або
![]() ділится на
ділится на
![]() .
.
Наслідком цих тверджень є таке:
Якщо поліном
![]() з дійсними коефіцієнтами двома способами
розкладено на незвідні множники
з дійсними коефіцієнтами двома способами
розкладено на незвідні множники
![]() то
то
–
![]() ;
;
– після відповідного впорядкування вірними будуть такі рівності:
![]()
Останнє твердження забезпечує
єдиність
розкладання полінома
![]() на незвідні множники. З
урахуванням того, що деякі незвідні
множники можуть входити до розкладання
полінома
на незвідні множники. З
урахуванням того, що деякі незвідні
множники можуть входити до розкладання
полінома
![]() не однократно, таке єдине подання буде
мати вигляд
не однократно, таке єдине подання буде
мати вигляд
![]() .
.
У зв’язку з тим, що в розкладанні врахована кратність входження незвідних поліномів, розв’язання задачі розкладання на незвідні множники почнемо з задачі розкладання на кратні множники.
Розглянемо алгоритм розкладання полінома на кратні множники.
Будемо вважати, що в розкладання
![]() поліноми входять з кратностями від 1
до n
включно. Позначимо
поліноми входять з кратностями від 1
до n
включно. Позначимо
– через
![]() добуток всіх поліномів, які входять у
добуток всіх поліномів, які входять у
![]() з кратністю 1. Поліноми, що входять до
з кратністю 1. Поліноми, що входять до
![]() можуть мати степені від 1 до n;
можуть мати степені від 1 до n;
– через
![]() добуток всіх поліномів, які входять у
добуток всіх поліномів, які входять у
![]() з кратністю 2.
з кратністю 2.
…………………………………
– через
![]() добуток всіх поліномів, які входять у
добуток всіх поліномів, які входять у
![]() з кратністю
з кратністю
![]() .
.
Тоді початкове розкладання
полінома
![]() на кратні множники буде виглядати так:
на кратні множники буде виглядати так:
![]()
На першому етапі знайдемо
максимальну кратність поліномів, що
входять до розкладання
![]() .
Позначимо її
.
Позначимо її
![]() .
.
Етап І.
1. а) Знаходимо
похідну від
![]() за змінною
за змінною
![]() :
:
![]() ,
,
де
![]() - поліном, який залишився в дужках після
виносу спільного множника.
- поліном, який залишився в дужках після
виносу спільного множника.
б) Знаходимо НСД між
![]() і
і
![]() :
:
![]()
Степінь
![]() менша за степінь
менша за степінь
![]() .
.
2. а) Знаходимо
похідну від
![]() за змінною
за змінною
![]() :
:
![]()
б) Знаходимо НСД між
![]() і
і
![]() :
:
![]()
Степінь
![]() менша за степінь
менша за степінь
![]() .
.
…………………………………….
S. .
а) Знаходимо похідну від
![]() за змінною
за змінною
![]() :
:
![]()
б) Знаходимо НСД між
![]() і
і
![]() :
:
![]()
Процес знаходження спільних дільників закінчено.
Максимальна кратність
входження поліномів у розкладання
![]() становить
становить
![]() .
.
Розкладання можна записати більш точно
![]()
При цьому
![]() - добуток ненульових поліномів нульового
степеня.
- добуток ненульових поліномів нульового
степеня.
Етап 2.
Виділяємо із знайдених
спільних дільників добуток складових
![]() в
першому степені.
в
першому степені.
1.

2.

…………………………….
S-1.

S.
![]()
На останньому кроці другого
етапу знайшли поліном, який є добутком
поліномів, які входять в розкладання
![]() з кратністю
з кратністю
![]() -
-
![]() .
.
Етап 3.
Діленням
![]() знаходимо складові
знаходимо складові
![]() в розкладанні полінома
в розкладанні полінома
![]() на кратні множники.
на кратні множники.
1.
![]()
2.
![]()
…………………………….
S-1.
![]()
Розкладання на кратні множники
відбулося. Залишилось перевірити, чи є
поліноми
![]() незвідними для
незвідними для
![]() .
.
Приклад.
Відокремити кратні множники поліному.
![]()
Розв’язання.
Етап І.
1. а) Знаходимо
похідну від
![]() за змінною
за змінною
![]() :
:
![]()
![]()
б) Знаходимо НСД між
![]() і
і
![]() :
:
-
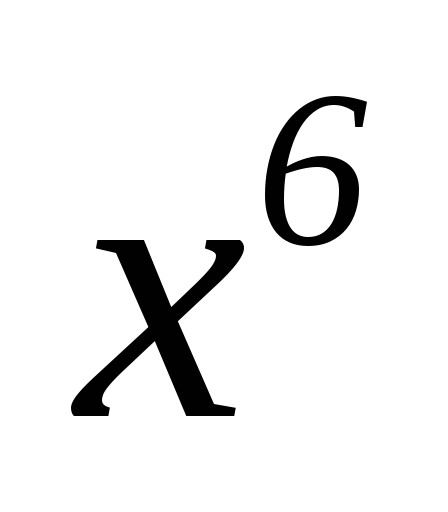


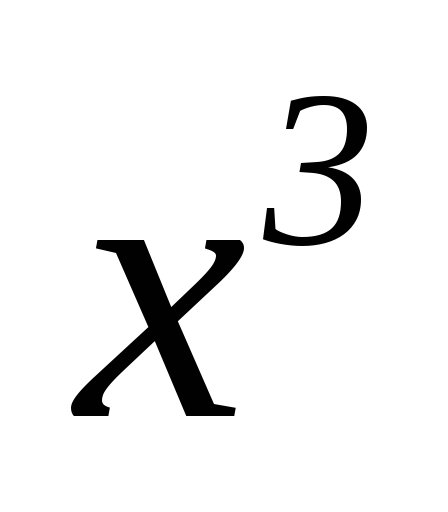









_1
0
-6
-4
9
12
4
1
0
-4
-2
3
2
1
0
-4
-2
3
2
0
1
:(-2)
-2
-2
6
10
4
1
1
-3
-5
-2
Перша остача
![]()
-


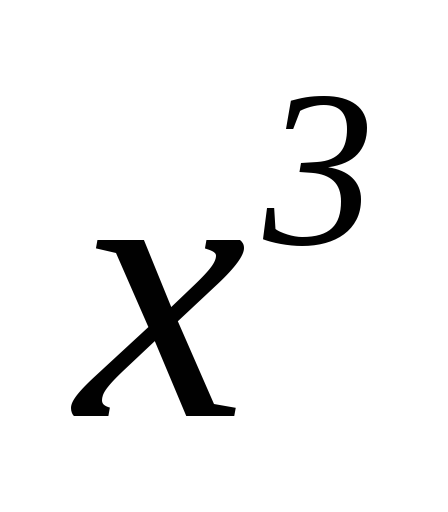





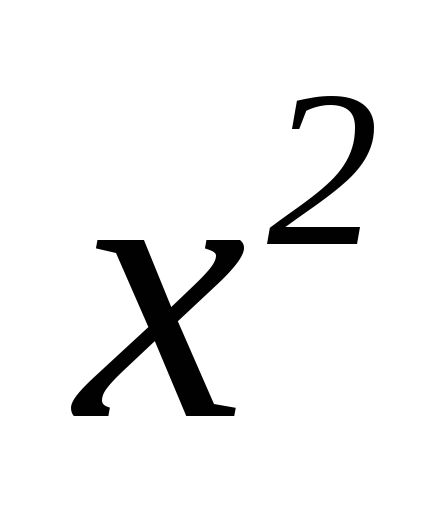


_1
0
-4
-2
3
2
1
1
-3
-5
-2
1
1
-3
-5
-2
0
1
-1
_-1
-1
3
5
2
-1
-1
3
5
2
0
0
0
0
0
![]()
![]()
2. а) Знаходимо
похідну від
![]() :
:
![]()
б) Знаходимо НСД між
![]() і
і
![]() :
:
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
-3 |
-5 |
-2 |
4 |
3 |
-6 |
-5 |
|
4 |
_4 |
4 |
-12 |
-20 |
-8 |
1 |
1 |
|
|
|
|
4 |
3 |
-6 |
-5 |
0 |
|
|
|
|
|
|
0 |
1 |
-6 |
-15 |
-8 |
|
|
|
|
|
|
4 |
_4 |
-24 |
-60 |
-32 |
|
|
|
|
|
|
|
4 |
3 |
-6 |
-5 |
|
|
|
|
|
|
|
0 |
-27 |
-54 |
-27 |
|
|
|
|
|
|
|
:(-27) |
1 |
2 |
1 |
|
|
|
|
Перша остача
![]()
|
|
|
|
|
|
|
|
|
_4 |
3 |
-6 |
-5 |
1 |
2 |
1 |
|
4 |
8 |
4 |
|
4 |
-5 |
|
|
|
_-5 |
-10 |
-5 |
|
|
|
|
|
-5 |
-10 |
-5 |
|
|
|
|
|
0 |
0 |
0 |
|
|
|
![]()
![]()
3. а) Знаходимо
похідну від
![]() :
:
![]()
![]()
б) Знаходимо НСД між
![]() і
і
![]() :
:
![]()
4. а)
Знаходимо похідну від
![]() за змінною
за змінною
![]() :
:
![]()
б) Знаходимо НСД між
![]() і
і
![]() :
:
![]()
Процес знаходження спільних дільників закінчено.
Максимальна кратність
входження поліномів у розкладання
![]() становить
становить
![]() .
.
Розкладання можна записати більш точно
![]()
При цьому
![]() - добуток ненульових поліномів нульового
степеня.
- добуток ненульових поліномів нульового
степеня.
Етап 2.
Виділяємо із знайдених
спільних дільників добуток складових
![]() в
першому степені.
в
першому степені.
1. Ділимо поліном на перший НСД.
![]() на
на
![]() .
.
-












1
0
-6
-4
9
12
4
1
1
-3
-5
-2
1
1
-3
-5
-2
1
-1
-2
0
-1
-3
1
11
12
4



-1
-1
3
5
2
0
0
-2
-2
6
10
4
-2
-2
6
10
4
0
0
0
0
0

2. Ділимо
![]() на
на
![]() .
.
-







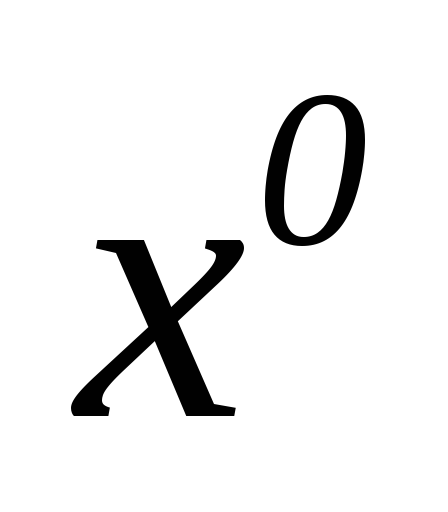
1
1
-3
-5
-2
1
2
1
1
2
1
1
-1
-2
0
-1
-4
-5
-2



-1
-2
-1
0
0
-2
-4
-2
-2
-4
-2
0
0
0

3.

4.
![]()
Незвідний поліном
![]() входить до розкладання поліному у 4-му
степені.
входить до розкладання поліному у 4-му
степені.
Етап 3.
Діленням
![]() знаходимо складові
знаходимо складові
![]() в розкладанні полінома
в розкладанні полінома
![]() на кратні множники.
на кратні множники.
1.
![]() ; 2.
; 2.
![]()
3.
![]()
Розкладання на кратні множники відбулося.
![]()
Поліном розклали і на кратні, і на незвідні множники, оскільки біноми, на які відбулося розкладання, є незвідними поліномами.
Коренями даного поліному
будуть числа
![]()
