
- •Обов’язкова контрольна робота №2 поліноми
- •1 Кубічні рівняння.
- •Індивідуальне завдання 1.
- •2 Обчислення значення полінома та його похідних у точці.
- •1. Розкладання полінома за степенями бінома
- •2. Обчислення похідних полінома в даній точці .
- •Індивідуальне завдання 2.1
- •3 Подільність поліномів. Нсд двох поліномів. Знаходження нсд за алгоритмом Евкліда. Подання нсд через лінійну комбінацію поліномів.
- •Поліном нульового степеня є дільником будь якого полінома степеня .
- •Індивідуальне завдання 2.2
- •4 Розкладання полінома на кратні та незвідні множники.
- •Індивідуальне завдання 3.
- •5. Побудова полінома найменшого степеня за відомими коренями.
- •Індивідуальне завдання 4.
Індивідуальне завдання 2.1
Для поліномів
![]() та
та
![]() використовуючи схему
Горнера знайти значення поліномів та
їх похідних в точці
використовуючи схему
Горнера знайти значення поліномів та
їх похідних в точці
![]() ,
разкласти поліноми за степенями біному
,
разкласти поліноми за степенями біному
![]() .
.
-
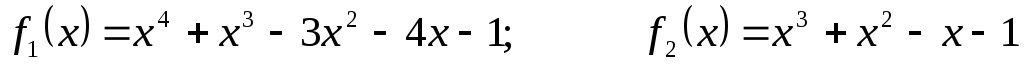 ;
;
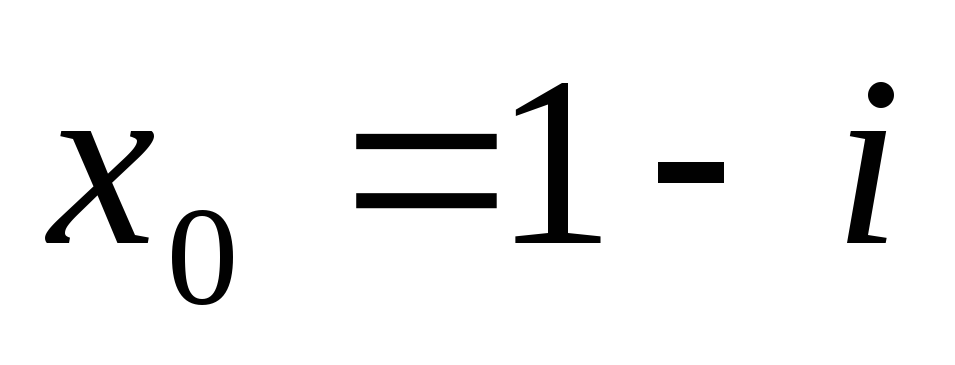
-
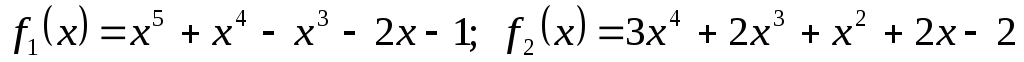 ;
;
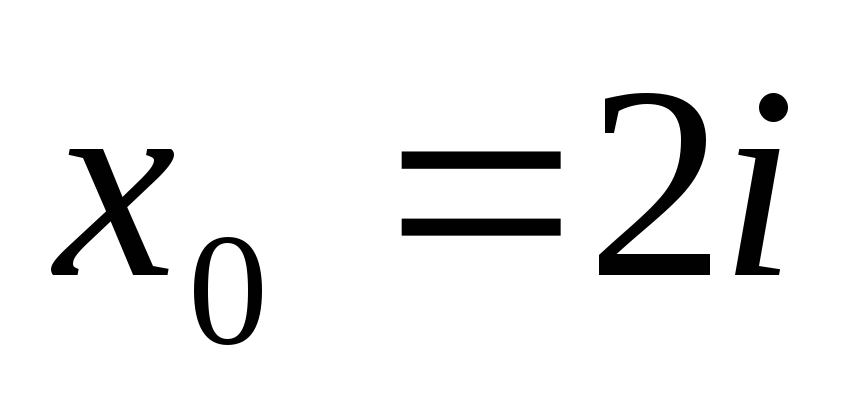
-
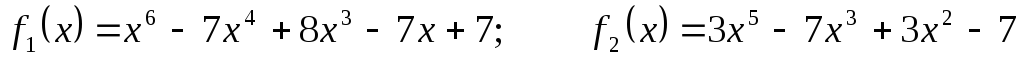 ;
;
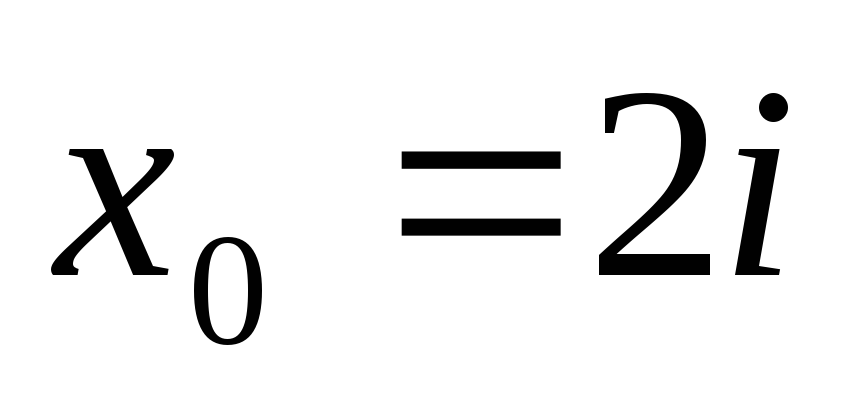
-
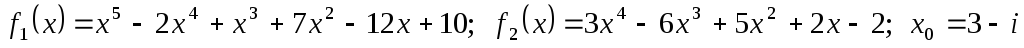
-
 ;
;
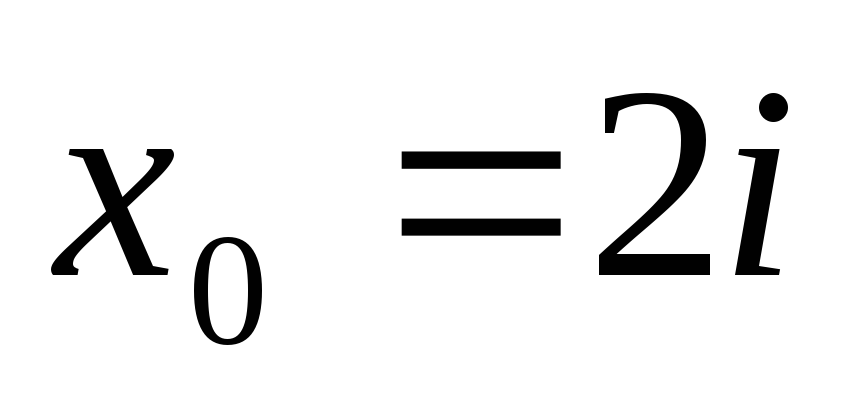
-
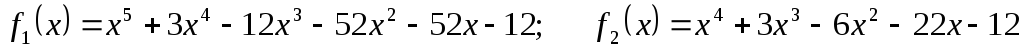 ;
; -
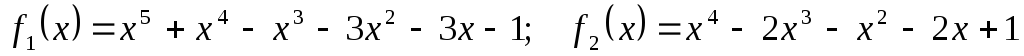 ;
;
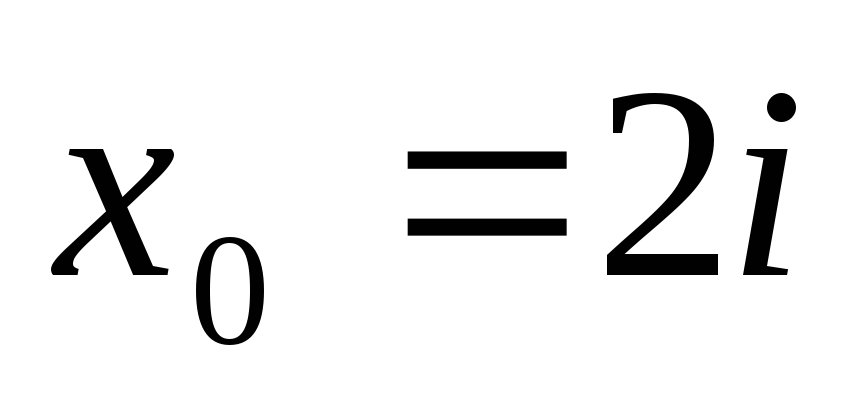
-
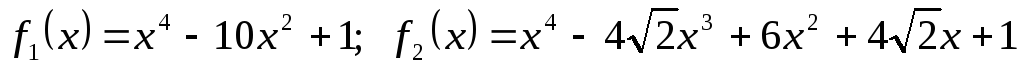 ;
;
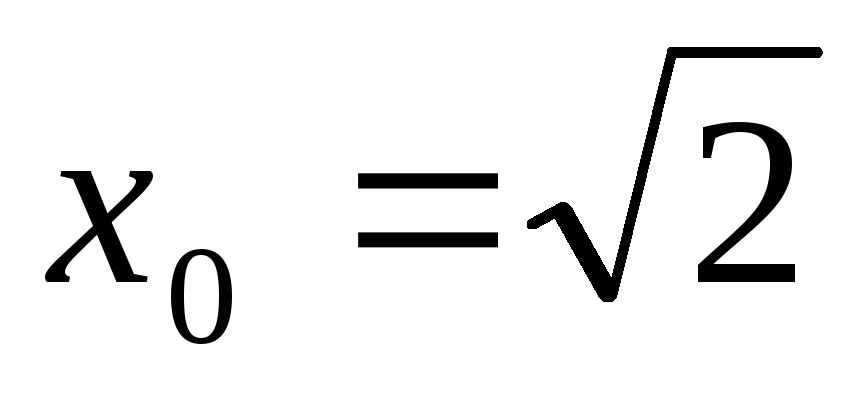
-
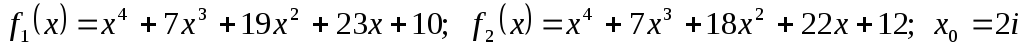
-
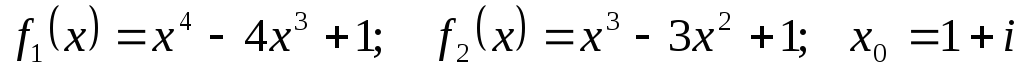
-
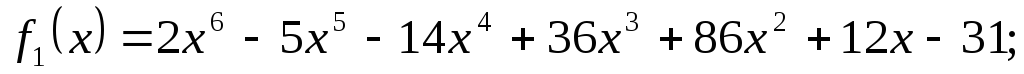
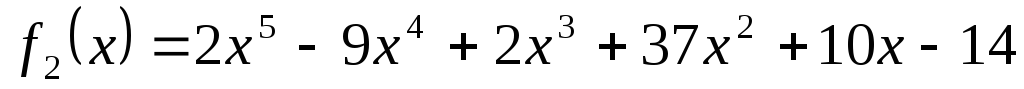 ;
;
-
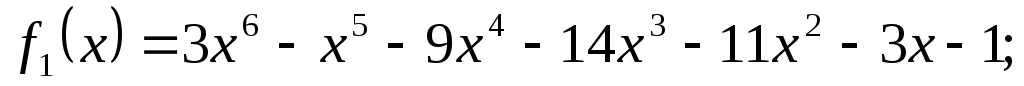
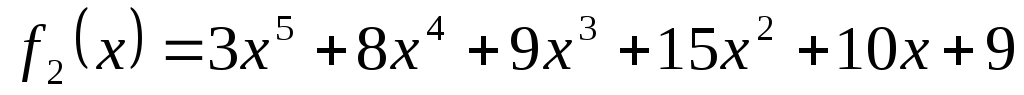
-
 ;
;
-
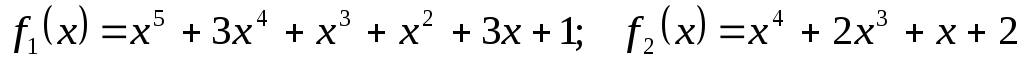 ;
;
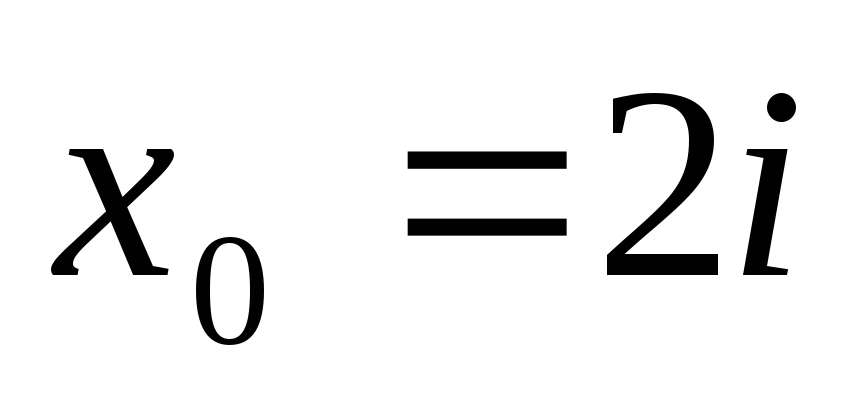
-

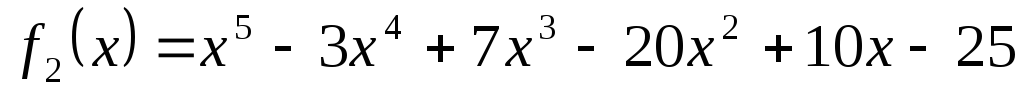 ;
;
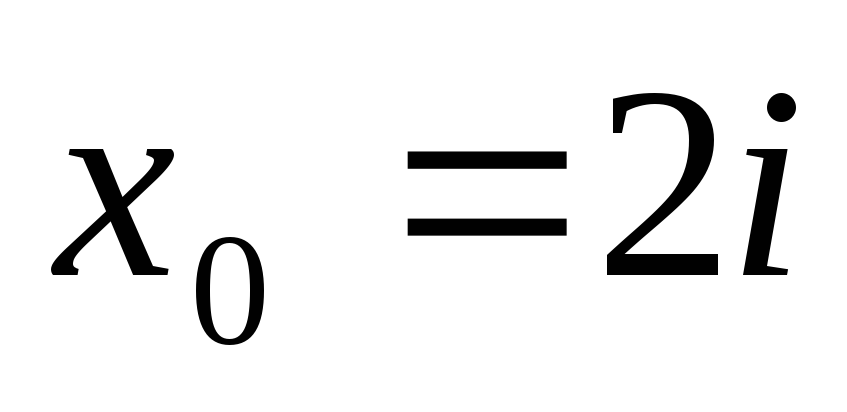
-
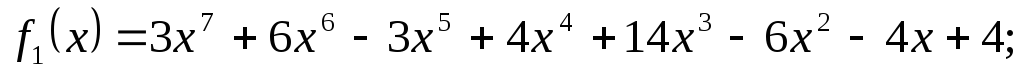
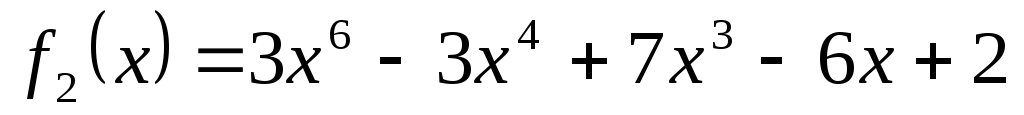 ;
;
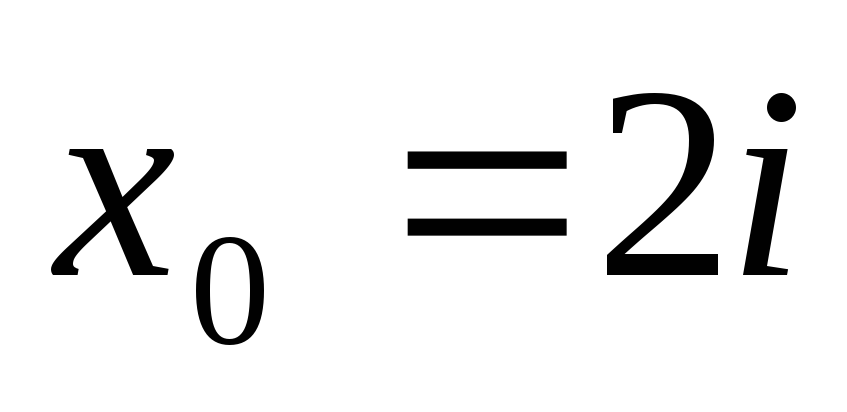
-

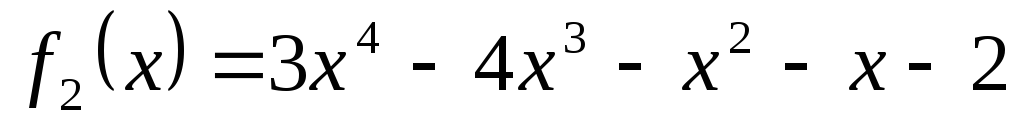 ;
;
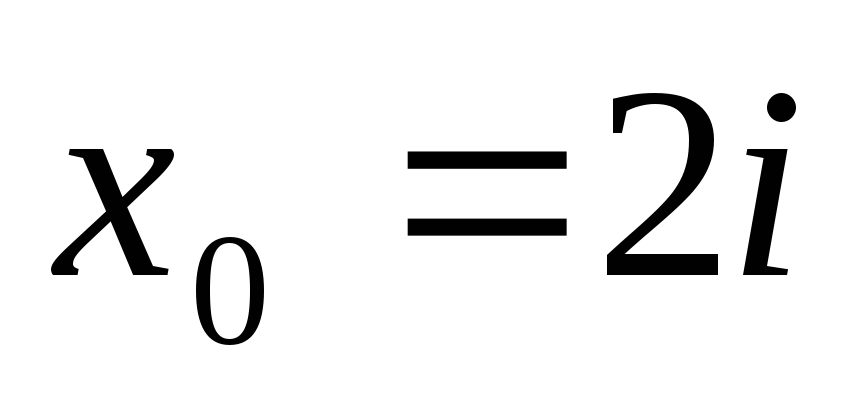
-
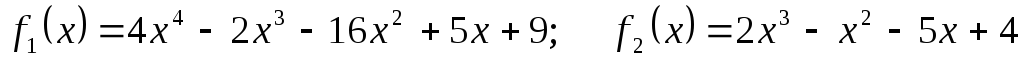 ;
;

-
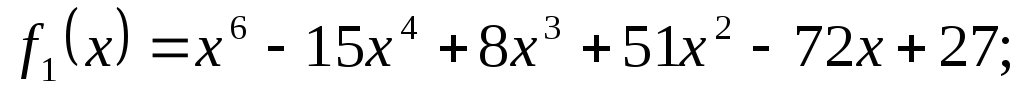
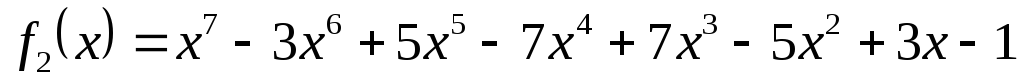 ;
;
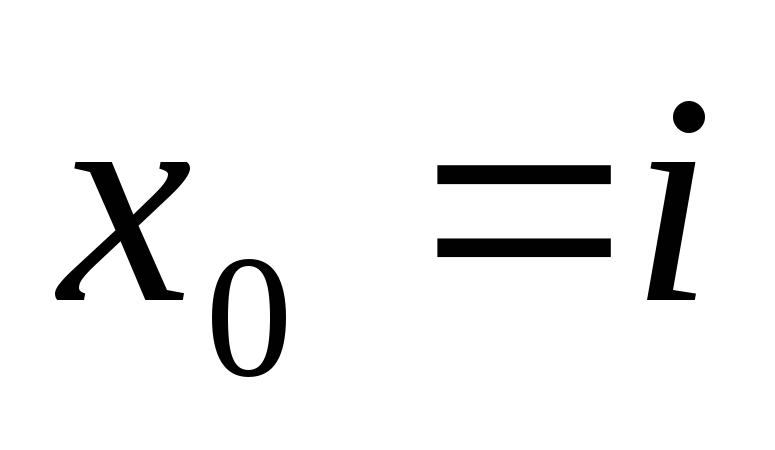
-
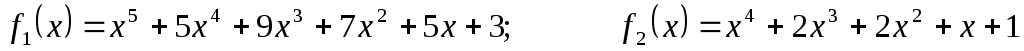
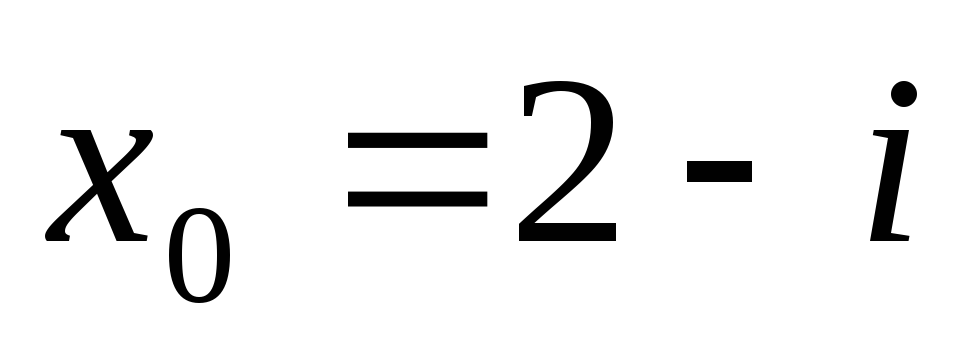 ;
; -
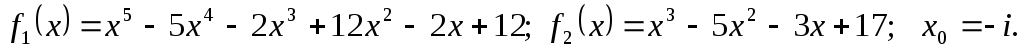
-
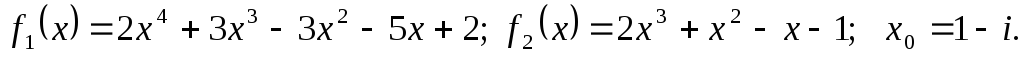
-

-
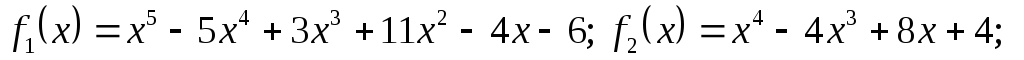

-
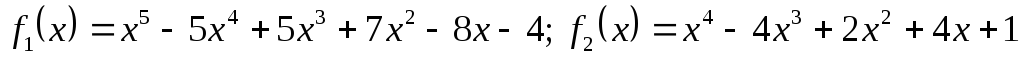
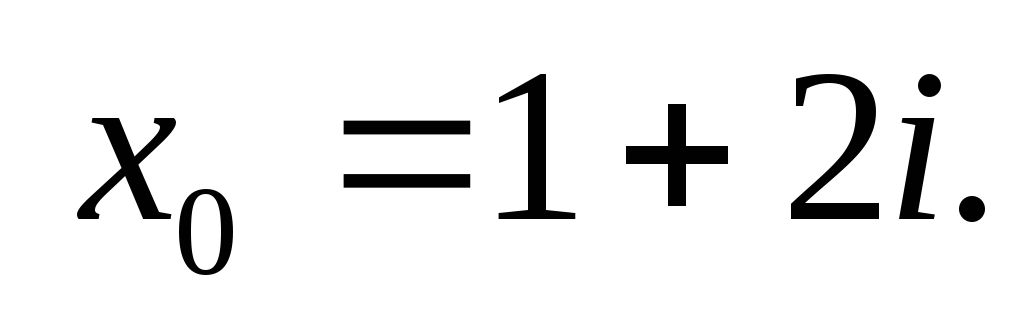
-
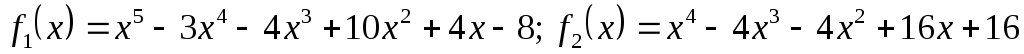
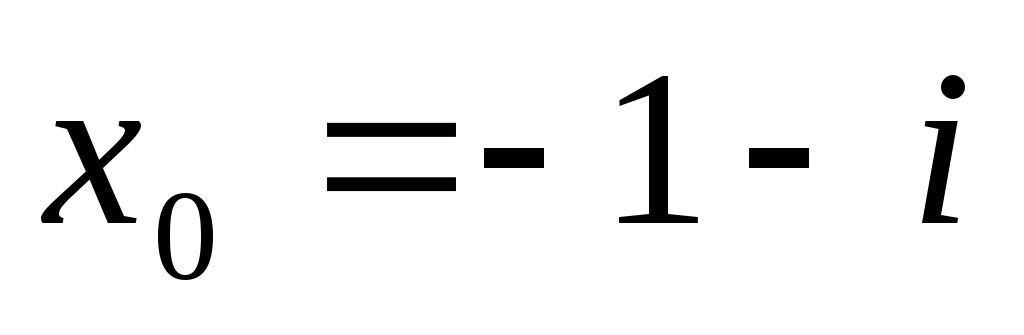
-

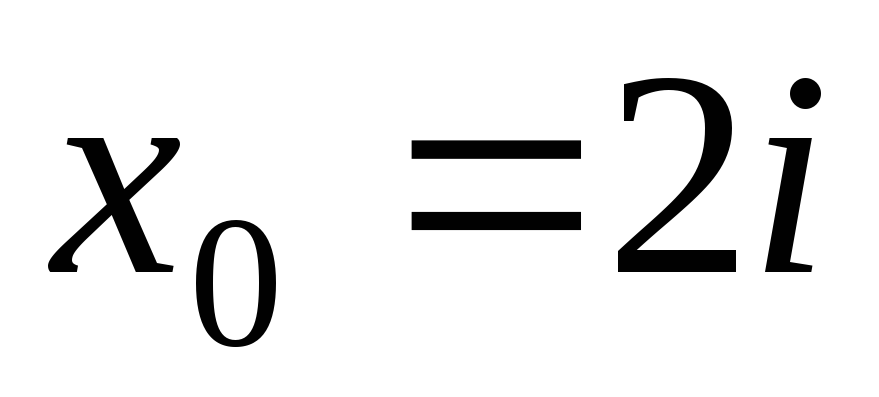
-
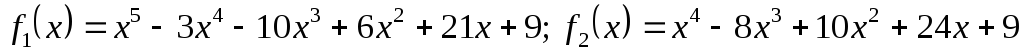

-

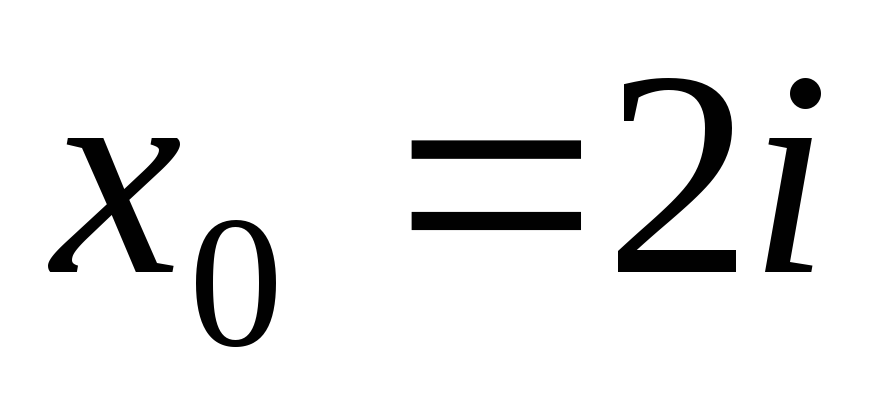
-
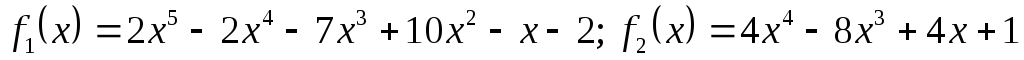
3 Подільність поліномів. Нсд двох поліномів. Знаходження нсд за алгоритмом Евкліда. Подання нсд через лінійну комбінацію поліномів.
Означення.
Розглядаються два ненульові
полінома
![]() та
та
![]() з дійсними коефіцієнтами степенів
з дійсними коефіцієнтами степенів
![]() та
та
![]() відповідно,
нехай
відповідно,
нехай
![]() .
.
Поліном
![]() ділиться без остачі на поліном
ділиться без остачі на поліном
![]() тоді і тільки тоді, якщо існує єдиний
поліном
тоді і тільки тоді, якщо існує єдиний
поліном
![]() такий, що
такий, що
![]() .
В цьому випадку поліном
.
В цьому випадку поліном
![]() називається дільником,
називається дільником,
![]() - часткою від
ділення полінома
- часткою від
ділення полінома
![]() на
поліном
на
поліном
![]() .
.
Якщо
![]() не ділить без остачі
не ділить без остачі
![]() ,
то завжди знайдуться такі поліноми
,
то завжди знайдуться такі поліноми
![]() та
та
![]() такі, що
такі, що
![]() подається єдиним образом у вигляді
подається єдиним образом у вигляді
![]() ,
,
![]() .
Таке подання називається діленням
полінома
.
Таке подання називається діленням
полінома
![]() з остачею.
Поліном
з остачею.
Поліном
![]() називається неповною
часткою, поліном
називається неповною
часткою, поліном
![]() - остачею від ділення
- остачею від ділення
![]() на
на
![]() .
.
Властивості подільності поліномів.
-
Якщо поліном
 ділиться на поліном
ділиться на поліном
 ,
а поліном
,
а поліном
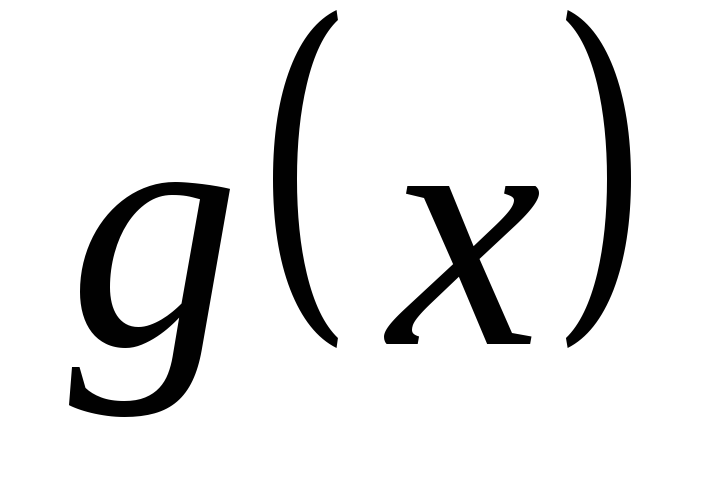 у свою чергу ділиться на поліном
у свою чергу ділиться на поліном
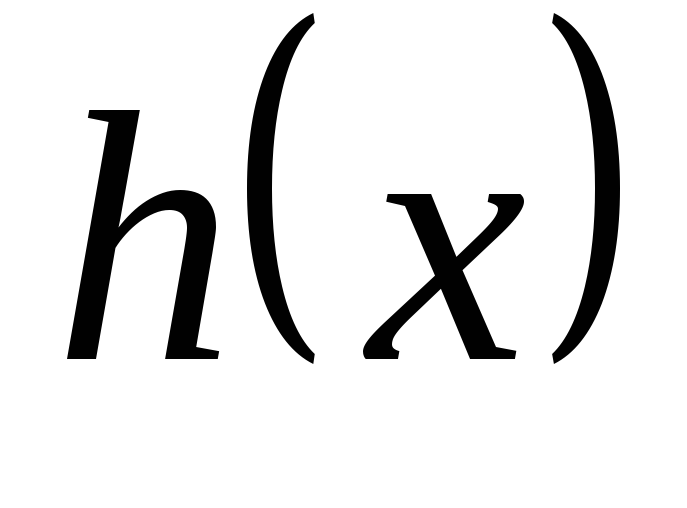 ,
то поліном
,
то поліном
 також ділиться на поліном
також ділиться на поліном
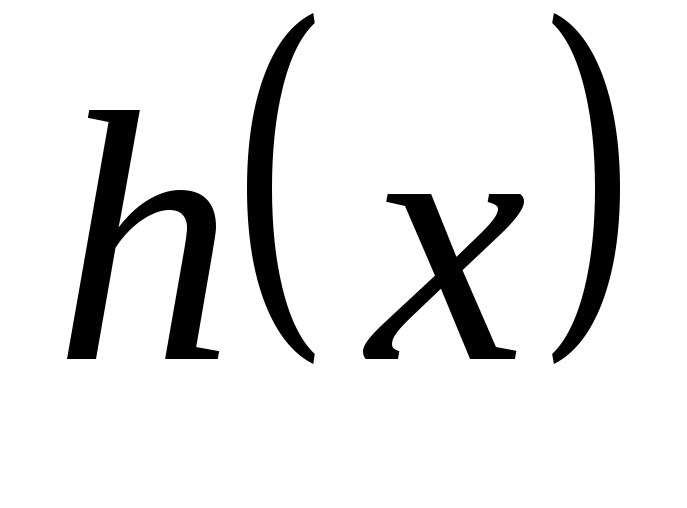
![]() .
.
-
Якщо поліноми
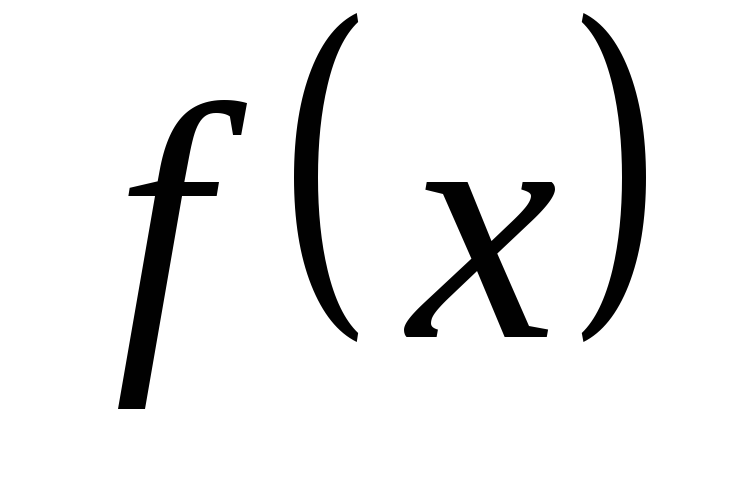 і
і
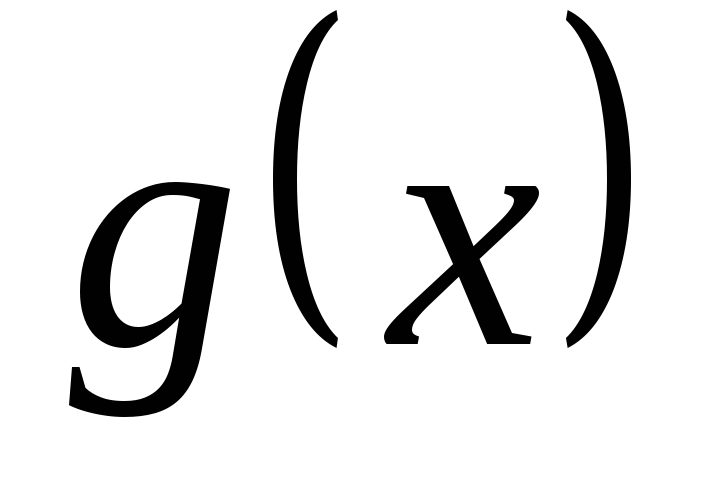 діляться на поліном
діляться на поліном
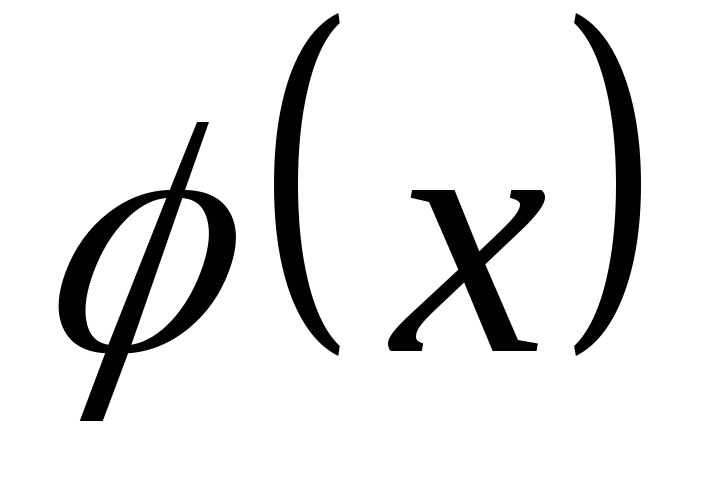 ,
то сума та різниця цих поліномів теж
ділиться на
,
то сума та різниця цих поліномів теж
ділиться на
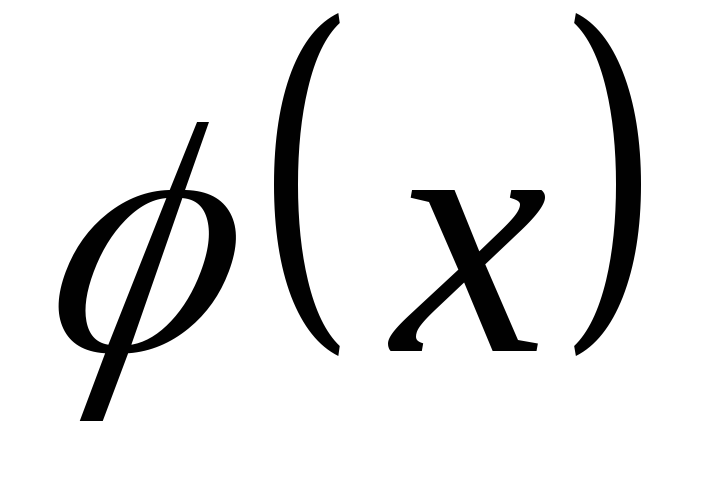
![]() .
.
-
Якщо поліном
 ділиться на поліном
ділиться на поліном
 ,
то добуток
,
то добуток
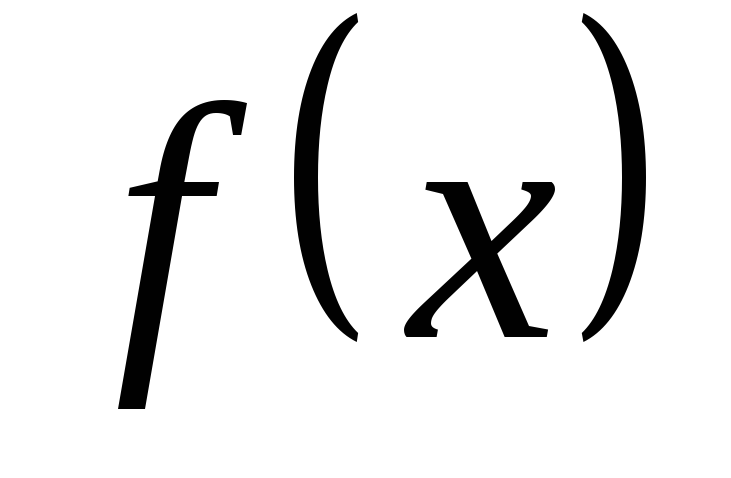 на довільний поліном
на довільний поліном
 теж ділиться на
теж ділиться на
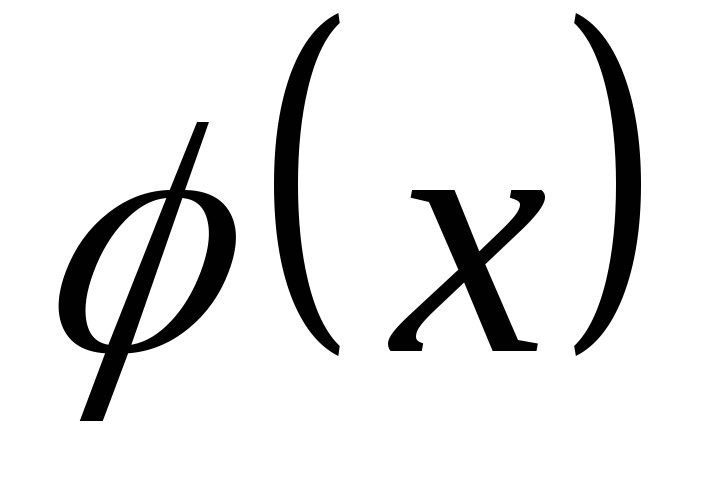
![]() .
.
-
Якщо кожний з поліномів
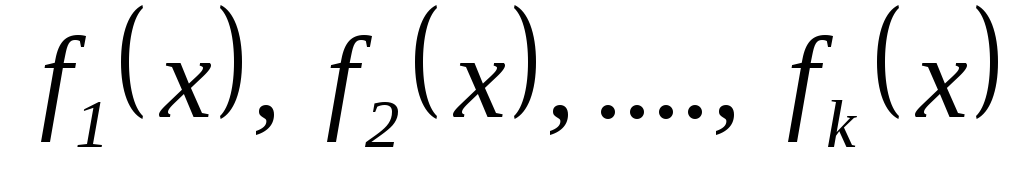 ділиться на поліном
ділиться на поліном
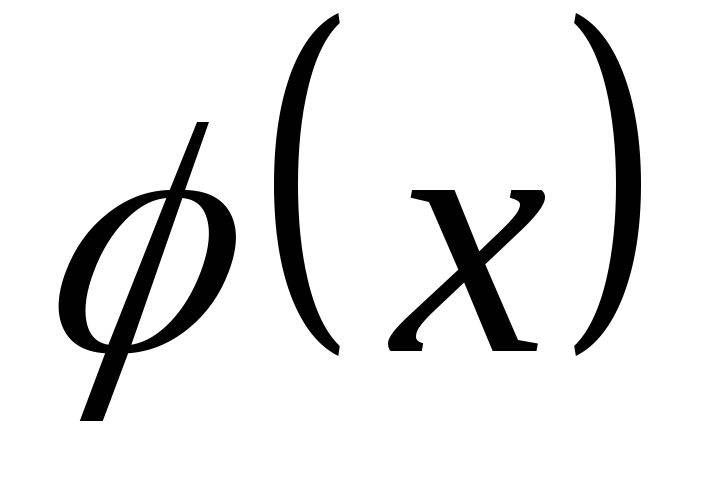 ,
то на
,
то на
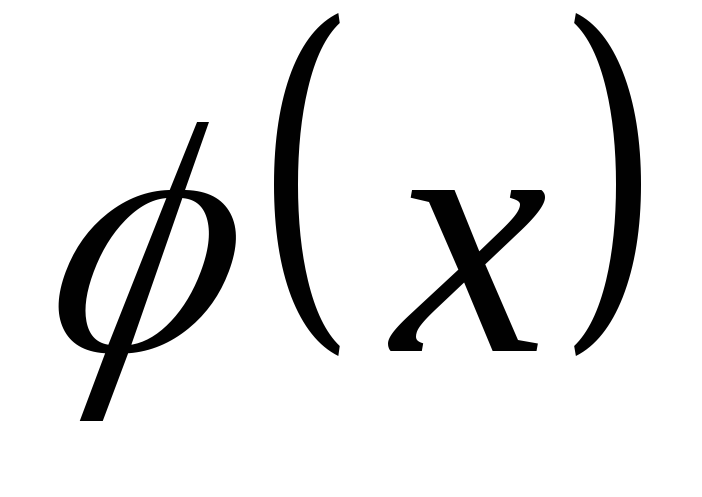 ділиться лінійна комбінація цих
поліномів
ділиться лінійна комбінація цих
поліномів
![]()
-
Поліном нульового степеня є дільником будь якого полінома степеня .
Означення
Поліном
![]() степеня
степеня
![]() ,
який ділиться тільки
на поліноми нульового степеня, на себе
самого та на поліном
,
який ділиться тільки
на поліноми нульового степеня, на себе
самого та на поліном
![]() називається незвідним
поліномом. Якщо
називається незвідним
поліномом. Якщо
![]() ділиться націло хоча б на один поліном
степеня
ділиться націло хоча б на один поліном
степеня
![]() ,
то такий поліном називається звідним.
,
то такий поліном називається звідним.
Означення
Поліном
![]() називається спільним
дільником поліномів
називається спільним
дільником поліномів
![]() та
та
![]() якщо він є дільником для кожного з цих
поліномів.
якщо він є дільником для кожного з цих
поліномів.
Очевидно, що два полінома завжди будуть мати за спільний дільник будь який поліном 0-го степеня.
Якщо ненульові поліноми
![]() та
та
![]() мають декілька спільних дільників із
ненульовими степенями, то серед них
можна обрати найбільший дільник.
мають декілька спільних дільників із
ненульовими степенями, то серед них
можна обрати найбільший дільник.
Означення
Поліном
![]() називається найбільшим
спільним дільником ненульових поліномів
називається найбільшим
спільним дільником ненульових поліномів
![]() та
та
![]() (НСД) якщо він є спільним
дільником цих поліномів і в свою чергу
ділиться на усі інші дільники цих
поліномів. Позначається НСД
(НСД) якщо він є спільним
дільником цих поліномів і в свою чергу
ділиться на усі інші дільники цих
поліномів. Позначається НСД
![]() .
.
Якщо ненульові поліноми
![]() та
та
![]() мають за спільні дільники тільки поліноми
0-го степеня, то такі поліноми називаються
взаємно простими.
мають за спільні дільники тільки поліноми
0-го степеня, то такі поліноми називаються
взаємно простими.
Алгоритм Евкліда для
знаходження НСД двох ненульових поліномів
![]() та
та
![]() .
.
Розглядаємо два ненульових
полінома
![]() та
та
![]() степенів
степенів
![]() та
та
![]() відповідно,
нехай
відповідно,
нехай
![]() .
.
1. Ділимо
![]() на
на
![]() .
.
Якщо
![]() ,
то
,
то
![]() - НСД знайдено,
- НСД знайдено,
інакше
![]() .
.
В останньому випадку з
властивості 4 подільності поліномів
спільний дільник поліномів
![]() та
та
![]() є також дільником остачі
є також дільником остачі
![]() .
Тобто НСД між
.
Тобто НСД між
![]() та
та
![]() співпадає з НСД між
співпадає з НСД між
![]() та
та
![]() .
Можна зробити перехід
до розшуку НСД між
.
Можна зробити перехід
до розшуку НСД між
![]() та
та
![]() .
При цьому степінь поліномів зменшується.
.
При цьому степінь поліномів зменшується.
2. Ділимо
![]() на
на
![]() .
.
Якщо
![]() ,
то
,
то
![]() - НСД знайдено,
- НСД знайдено,
інакше
![]() .
.
Переходимо до розшуку НСД
між
![]() та
та
![]() .
При цьому степінь поліномів знову
зменшується.
.
При цьому степінь поліномів знову
зменшується.
3. ![]() .
.
………………….
k-1. ![]() .
.
k. ![]() .
.
k+1. ![]() .
.
Оскільки степінь поліномів
![]() на кожному кроці зменшується, то процес
поетапного ділення завжди буде скінченим,
граничним значення остач буде поліном
0-го степеня.
на кожному кроці зменшується, то процес
поетапного ділення завжди буде скінченим,
граничним значення остач буде поліном
0-го степеня.
З останнього кроку видно, що
![]() .
.
Простежуючи поступово вгору
ланцюжок ділень, можна зробити висновок,
що
![]()
Отже, можна зробити висновок,
що в алгоритмі Евкліда
НСД між поліномами
![]() та
та
![]() буде дорівнювати останній ненульовій
остачі
буде дорівнювати останній ненульовій
остачі
![]() з
ланцюжка поступових ділень.
з
ланцюжка поступових ділень.
Якщо НСД між поліномами
![]() та
та
![]() є поліном 0-го степеня - число
є поліном 0-го степеня - число
![]() ,
то з урахуванням властивості 5 подільності
поліномів можна стверджувати, що в
такому випадку НСД між
,
то з урахуванням властивості 5 подільності
поліномів можна стверджувати, що в
такому випадку НСД між
![]() та
та
![]() дорівнює 1.
дорівнює 1.
Застосувавши властивість 5
подільності поліномів, до
![]() - полінома степеня, більшого за 0, можна
- полінома степеня, більшого за 0, можна
![]() подати таким чином:
подати таким чином:
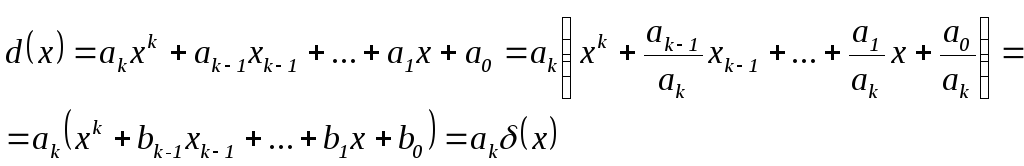
Скоротивши НСД на
![]() згідно властивості подільності поліномів
5, отримаємо, що
згідно властивості подільності поліномів
5, отримаємо, що
![]()
Висновки:
1. Алгоритм Евкліда є завжди скінченим.
2. За алгоритмом Евкліда знаходимо НСД двох поліномів з точністю до числа.
3.
![]() ,
де
,
де
![]() - поліном з коефіцієнтом біля старшого
степеня
- поліном з коефіцієнтом біля старшого
степеня
![]() .
.
4. Два полінома взаємно прості
тоді і тільки тоді, коли
![]() .
.
Приклад 1
За алгоритмом Евкліда найти
НСД між
![]() та
та
![]()
Розв’язання.
1. Ділимо
![]() на
на
![]() .
.
-

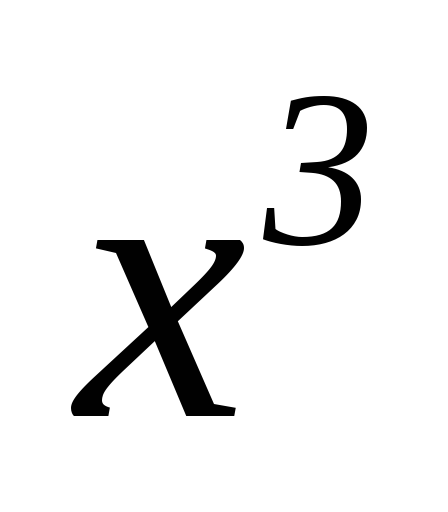
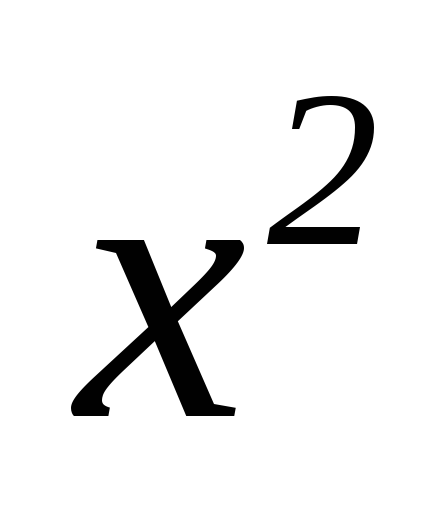
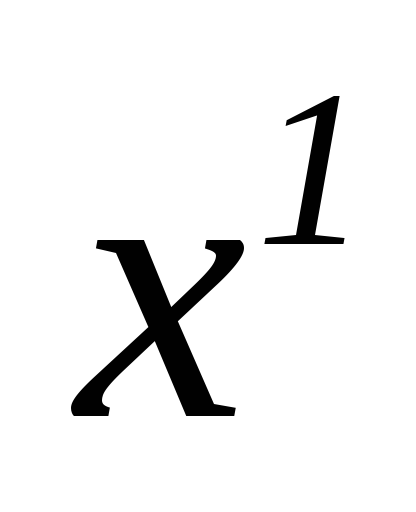
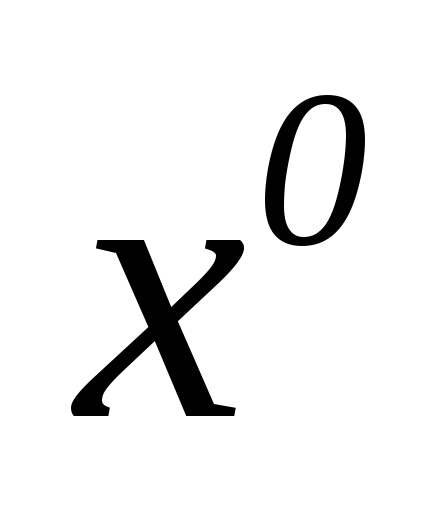
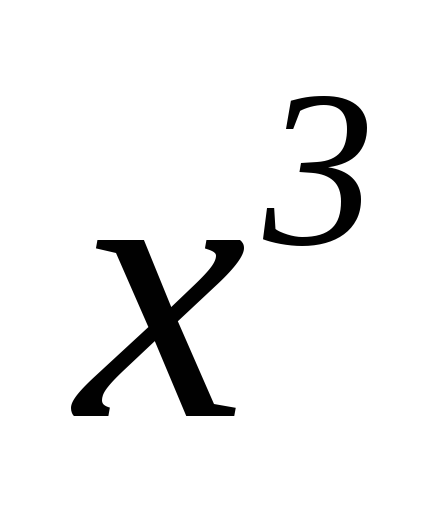
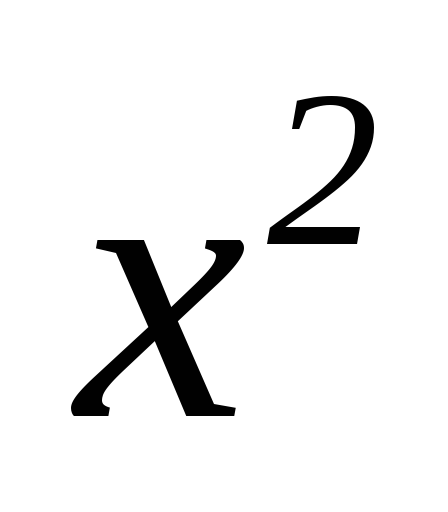
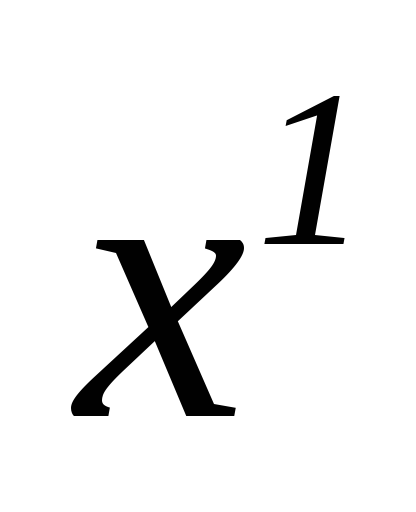
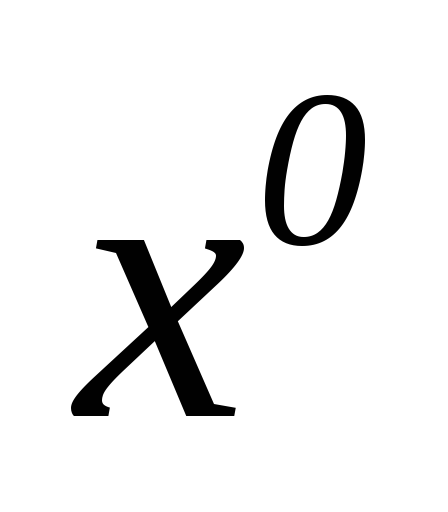
3
1
3
-1
-4
-3
3
10
2
-3
_ 3
9
-3
-12
-9
1
-1
3
10
2
-3
3
-1
-5
-9
-9
_-3
-15
-27
-27
-3
-10
-2
3
: (-5)
-5
-25
-30
1
5
6
![]() можна
подати так:
можна
подати так:
![]() ,
тобто
,
тобто
![]() ,
степінь остачі менша за степінь
,
степінь остачі менша за степінь
![]()
![]()
Оскільки нас цікавить НСД з точністю до числа, то ми можемо в процесі ділення множити поліном, що ділиться, на число а залишок скоротити на спільний для всіх його коефіцієнтів дільник.
Отже, за
![]() можна взяти
можна взяти
![]()
2. Ділимо
![]() на
на
![]() .
.
-
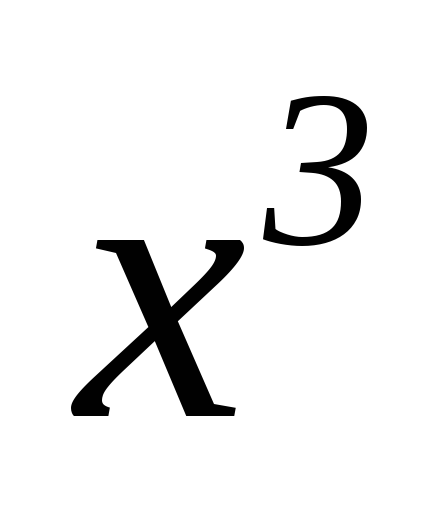
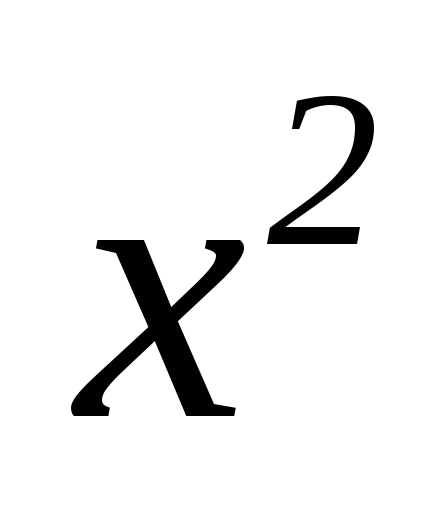
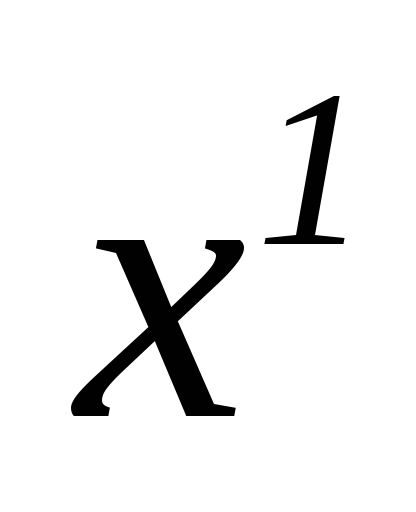
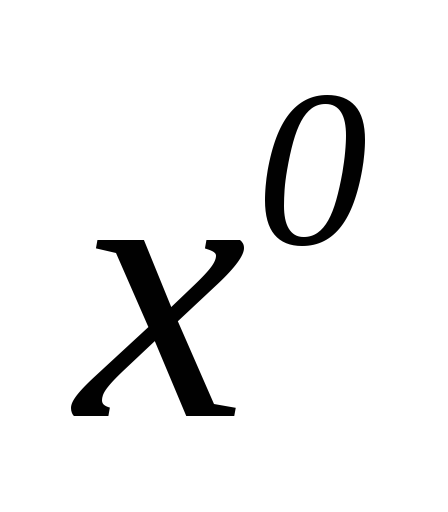

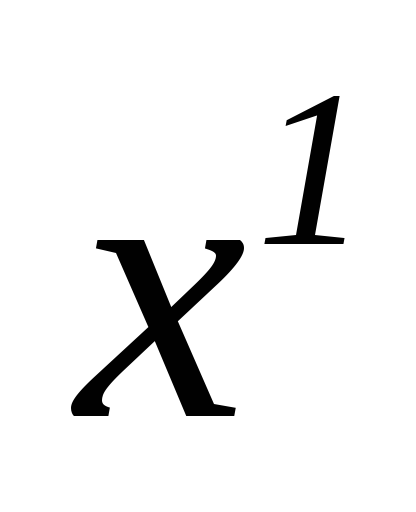
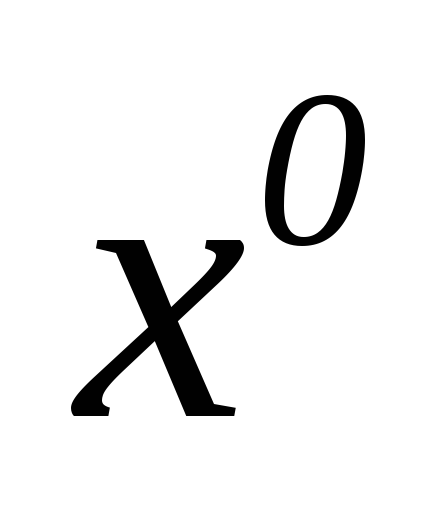
_ 3
10
2
-3
1
5
6
3
15
18
3
-5
_-5
-16
-3
-5
-25
-30
: 9
9
27
1
3
![]() можна подати так:
можна подати так:
![]() ,
тобто
,
тобто
![]() ,
степінь остачі менша за степінь
,
степінь остачі менша за степінь
![]()
![]()
3. Ділимо
![]() на
на
![]() .
.
-
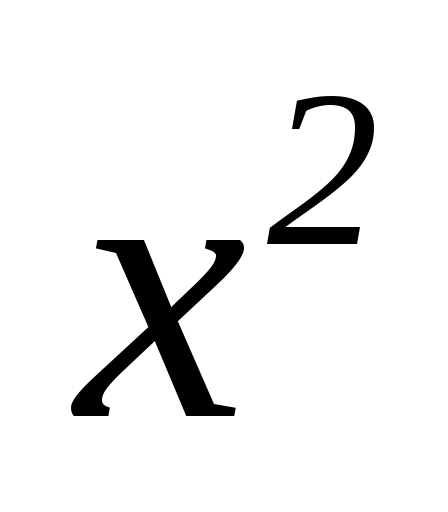

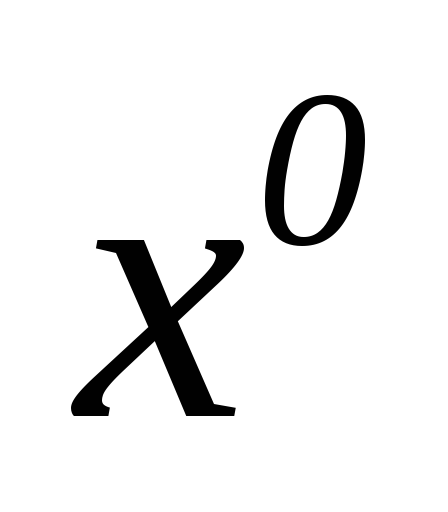
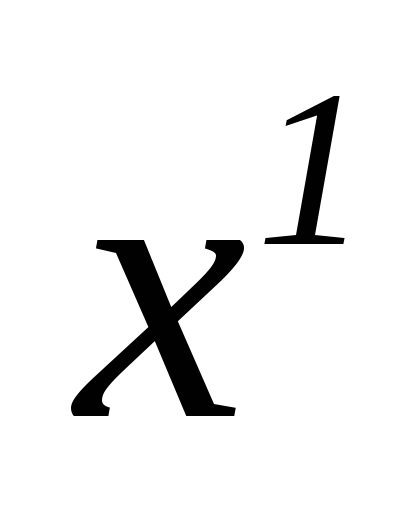
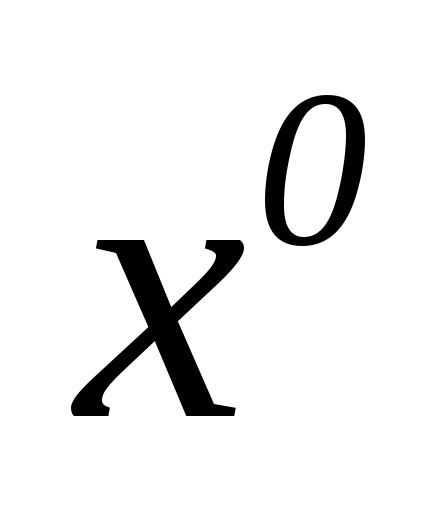
_ 1
5
6
1
3
1
3
1
2
_ 2
6
2
6
0
0
![]() можна подати так:
можна подати так:
![]() ,
тобто
,
тобто
![]() .
.
Процес поступового ділення
можна зупинити. Останній ненульовий
залишок ланцюжка ділень є
![]() .
.
Отже, за алгоритмом Евкліда
НСД між
![]() та
та
![]() дорівнює
дорівнює
![]() .
.
Відповідь.
![]()
Теорема про подання НСД двох поліномів лінійною комбінацією цих поліномів.
Якщо
![]() є найбільшим спільним дільником поліномів
є найбільшим спільним дільником поліномів
![]() та
та
![]() ,
то завжди можна знайти такі поліноми
,
то завжди можна знайти такі поліноми
![]() та
та
![]() ,
що
,
що
![]()
Якщо степені поліномів
![]() та
та
![]() більші за 0, то степінь полінома
більші за 0, то степінь полінома
![]() хоча б на 1 менший від степеня
хоча б на 1 менший від степеня
![]() ,
а степінь
,
а степінь
![]() на 1 менший від степеня
на 1 менший від степеня
![]() .
.
Доведення.
Довести цю теорему можна,
побудувавши поліноми
![]() та
та
![]() з
використанням ланцюжка ділень в алгоритмі
Евкліда.
з
використанням ланцюжка ділень в алгоритмі
Евкліда.
Будемо послідовно отримувати
вираз для
![]() ,
починаючи з передостаннього ділення.
,
починаючи з передостаннього ділення.
Відмітимо, що
![]() ,
де с
– коефіцієнт біля старшого степеня в
поліномі
,
де с
– коефіцієнт біля старшого степеня в
поліномі
![]() .
Використовуючи попередні ділення будемо
виключати з виразу для
.
Використовуючи попередні ділення будемо
виключати з виразу для
![]() всі остачі так, щоб у кінцевій формулі
залишилися тільки поліноми
всі остачі так, щоб у кінцевій формулі
залишилися тільки поліноми
![]() та
та
![]()
![]() ,
,
![]() ,
,
![]()
Поступово підставляючи в
вираз для
![]() значення остач
значення остач
![]() ,
отримаємо наприкінці ланцюжка зворотних
підстановок вираз
,
отримаємо наприкінці ланцюжка зворотних
підстановок вираз
![]() ,
або
,
або
![]() ,
що і потрібно було побудувати для
доведення теореми.
,
що і потрібно було побудувати для
доведення теореми.
Зауваження. Звернемо
увагу на те, що для побудови лінійного
подання НСД двох поліномів необхідні
не викривленні значення неповних часток
![]() .
Тому в ланцюжку ділень в алгоритмі
Евкліда
.
Тому в ланцюжку ділень в алгоритмі
Евкліда
- неможна множити на число поліном, що ділиться в середині процесу ділення;
- якщо на початку ділення є необхідність умножити на число поліном, що ділиться, це число необхідно урахувати при зворотному проходженні ланцюжка.
Приклад 2
Використовуючи ланцюжок
ділень з попереднього прикладу подати
лінійною комбінацією НСД поліномів
![]() та
та
![]() .
.
Розв’язання.
Розглянемо ланцюжок ділень з попереднього прикладу.
1. Ділення
![]() на
на
![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1 |
3 |
-1 |
-4 |
-3 |
3 |
10 |
2 |
-3 |
|
|
_3 |
9 |
-3 |
-12 |
-9 |
1 |
- 1/3 |
|
|
|
|
3 |
10 |
2 |
-3 |
|
|
|
|
|
|
|
|
_ -1 |
-5 |
-9 |
-9 |
|
|
|
|
|
|
|
-1 |
-3 1/3 |
- 2/3 |
1 |
|
|
|
|
|
: (-1 2/3) |
|
|
-1 2/3 |
-8 1/3 |
-10 |
|
|
|
|
|
|
|
|
1 |
5 |
6 |
|
|
|
|
Поліном
![]() подається так:
подається так:
![]()
Тобто
![]()
![]()
2. Ділення
![]() на
на
![]() .
.
![]()
![]()
![]()
3. Ділення
![]() на
на
![]() .
.
![]() ,
тобто
,
тобто
![]() ,
,
![]()
Отже,
![]()
Виконаємо обернену прогонку.
З ділення 2
маємо
![]() .
Підставимо до виразу для
.
Підставимо до виразу для
![]() :
:
![]()
З ділення 1
маємо
![]() .
Підставимо до виразу для
.
Підставимо до виразу для
![]() :
:

Отже маємо лінійне подання
НСД поліномів
![]() та
та
![]() :
:
![]()
Тобто, отримали, що
![]()
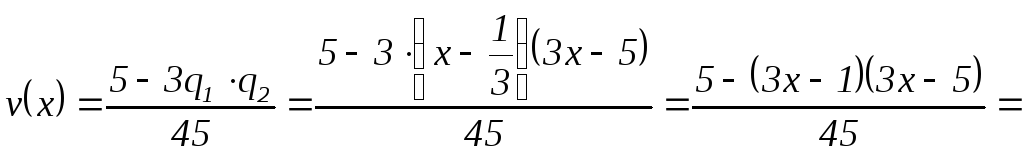
![]()
Перевірка
![]()
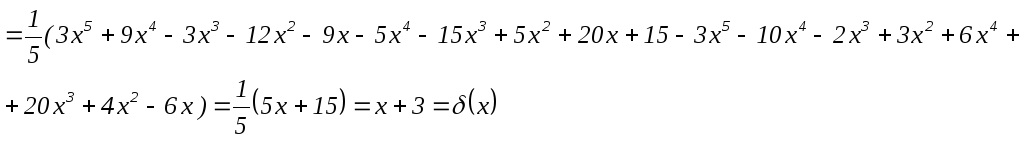
Висновок.
Перевірка показала, що отримана
лінійна комбінація поліномів дає НСД
поліномів
![]() та
та
![]() .
.
Значення функцій в розкладанні
НСД:
![]() .
.
