
- •Обов’язкова контрольна робота №2 поліноми
- •1 Кубічні рівняння.
- •Індивідуальне завдання 1.
- •2 Обчислення значення полінома та його похідних у точці.
- •1. Розкладання полінома за степенями бінома
- •2. Обчислення похідних полінома в даній точці .
- •Індивідуальне завдання 2.1
- •3 Подільність поліномів. Нсд двох поліномів. Знаходження нсд за алгоритмом Евкліда. Подання нсд через лінійну комбінацію поліномів.
- •Поліном нульового степеня є дільником будь якого полінома степеня .
- •Індивідуальне завдання 2.2
- •4 Розкладання полінома на кратні та незвідні множники.
- •Індивідуальне завдання 3.
- •5. Побудова полінома найменшого степеня за відомими коренями.
- •Індивідуальне завдання 4.
Індивідуальне завдання 1.
Знайти корені кубічного
рівняння
![]() за формулами Кардано
за формулами Кардано
Коефіцієнти
![]() ,
,
![]() ,
,
![]() наведені у таблиці
наведені у таблиці
-
Вариант
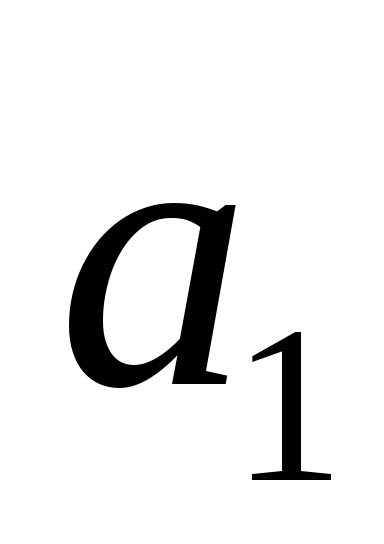
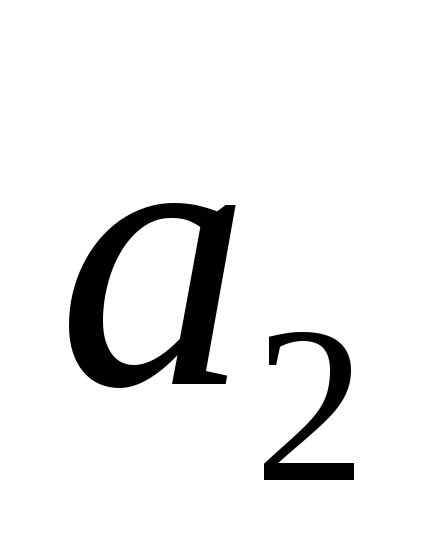

1
6
6
-13
2
6
3
-38
3
3
12
-16
4
-3
-9
-5
5
3
21
38
6
12
42
49
7
-9
24
-20
8
3
12
36
9
-6
6
-5
10
-6
18
-13
11
-12
45
-54
12
12
54
95
13
3
-9
-27
14
-3
21
-38
15
3
27
-31
16
9
24
16
17
-9
36
-28
18
3
-3
-14
19
-6
9
-4
20
-12
42
-31
21
3
-15
-52
22
9
18
28
23
6
30
25
24
6
6
5
25
12
45
50
26
-6
30
-63
27
-9
9
62
28
-3
-3
-4
29
-9
18
-28
30
-6
21
-52
2 Обчислення значення полінома та його похідних у точці.
Означення
Поліномом (многочленом, багаточленом) степеня n називається функція виду
![]() , (1)
, (1)
де
![]() ,
,
![]() - змінна, n
– максимальний степінь
входження змінної х
з ненульовим коефіцієнтом у функцію.
- змінна, n
– максимальний степінь
входження змінної х
з ненульовим коефіцієнтом у функцію.
Якщо коефіцієнти полінома є
дійсними числами, то кажуть, що поліном
заданий у множині
![]() .
Якщо коефіцієнти комплексні, то – у
множині
.
Якщо коефіцієнти комплексні, то – у
множині
![]() .
.
Для уособлення функції поліном
її часто позначають
![]() ,
де n
– показник степеня полінома.
,
де n
– показник степеня полінома.
Коренем
полінома
називається значення змінної
![]() ,
якщо
,
якщо
![]()
Основна теорема алгебри
Комплексний поліном степеня n > 0 має рівно n комплексних коренів, з урахуванням кратності.
Інакше кажучи, його можна розкласти на n лінійних множників
![]() - корені полінома. (2)
- корені полінома. (2)
Якщо
![]() є коренем полінома, то
є коренем полінома, то
![]() ,
тобто поліном
,
тобто поліном
![]() без остачі ділиться на біном
без остачі ділиться на біном
![]() .
Поліном
.
Поліном
![]() носить назву частка від
ділення
носить назву частка від
ділення
![]() на
на
![]()
В разі, коли деяке значення
змінної
![]() не є коренем полінома, ділення полінома
приймає вигляд
не є коренем полінома, ділення полінома
приймає вигляд
![]() , (3)
, (3)
де
![]() - неповна частка від
ділення
- неповна частка від
ділення
![]() на
на
![]() ,
,
![]() –
число, остача від ділення
–
число, остача від ділення
![]() на
на
![]() ,
,
![]() .
.
Розглянемо (3) більш докладно.
![]() (4)
(4)
Для обчислення значення
поліному у точці
![]() достатньо підставити це значення у
поліном. З правої частини (4) видно, що
достатньо підставити це значення у
поліном. З правої частини (4) видно, що
![]() .
.
Отже, значення
полінома в довільній точці
![]() дорівнює остачі від ділення полінома
дорівнює остачі від ділення полінома
![]() на біном
на біном
![]() .
.
Для знаходження остачі
![]() і коефіцієнтів поліному
і коефіцієнтів поліному
![]() розкриємо дужки у (4) і
прирівняємо коефіцієнти при рівних
степенях у правій і лівій частинах
рівності.
розкриємо дужки у (4) і
прирівняємо коефіцієнти при рівних
степенях у правій і лівій частинах
рівності.

Схематично такі розрахунки записуються у вигляді схеми Горнера
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
Приклад 1
Обчислити значення полінома
![]() в точці
в точці
![]() .
.
Розв’язання.
Маємо поліном п’ятого степеня. Коефіцієнти полінома є такими:
![]() .
.
Складемо схему Горнера ділення
![]() на біном
на біном
![]() :
:
|
|
3 |
0 |
0 |
-2 |
0 |
6 |
|
-2 |
3 |
(-2)·3+0=-6 |
(-2)·(-6)+0=12 |
(-2)·12+(-2)=-26 |
(-2)·(-26)+0=52 |
(-2)·52+6=-98 |
Отже,
![]()
Неповна частка від ділення
![]() на
на
![]() буде
буде
![]()
Отже можна записати
![]()
Застосування схеми Горнера.
