-25-

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

КАФЕДРА ТЕХНИЧЕСКОЙ КИБЕРНЕТИКИ И ИНФОРМАТИКИ

Автоматизация управления двигателем постоянного тока с независимым возбуждением

Пояснительная записка к курсовому проекту

по курсу «Технические средства автоматизации управления»

Выполнил:

студент группы УИТ-22

Левин Е.Г.

Проверил:

доцент кафедры ТКИ

Ушакова О.В.

Саратов 2012

Цель работы:определение параметров и характеристик переходного процесса заданного двигателя постоянного тока независимого возбуждения при автоматизации пуска и торможения с последующей разработкой схемы автоматического управления.

Курсовая работа направлена на закрепление теоретических знаний, полученных при изучении дисциплины Технические средства автоматизации и управления и приобретении практических навыков при решении конкретных технических задач.

Содержание

ЗАДАНИЕ

1. РАСЧЕТ ОСНОВНЫХ ПАРАМЕТРОВ СИСТЕМЫ

2. РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПРИ ПУСКЕ И ДИНАМИЧЕСКОМ ТОРМОЖЕНИИ

3. РАЗРАБОТКА ПРИНЦИПИАЛЬНОЙ ЭЛЕКТРИЧЕСКОЙ СХЕМЫ УПРАВЛЕНИЯ ДВИГАТЕЛЕМ

ЗАКЛЮЧЕНИЕ

СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ

Задание Вариант №18

Р_2Н=0,76кВт

U_H=220B

I_яН=4,5А

n_H=1000об/мин

R=5,32Ом

L=35мГн

J=40,8·10-3кг·м²

а=50%

1. Расчет основных параметров системы

1. . Математическая модель электромеханической системы

Рассмотрим электромеханическую систему, состоящую из двигателя постоянного тока с независимым возбуждением и исполнительного механизма ИМ. Приведем математическую модель этой системы. При составлении системы будем считать, что двигатель работает в ненасыщенном режиме.

Рассмотрим переходные процессы при пуске двигателя независимого возбуждения, подразумевая под пуском подключение якоря к сети постоянного тока U. Так как обмотка возбуждения такого двигателя постоянно включена под напряжение, то угловая скорость и направление вращения вала зависят лишь от значения и полярности напряжения, подаваемого к якорю.

Дифференциальное уравнение, описывающее поведение двигателя независимого возбуждения при переходном процессе запишется в следующем виде:

(1.1.1)

где L – индукция якоря;

- ток якоря.

Напряжение U уравновешивается ЭДС самоиндукции якоря , падением напряжения на активном сопротивленииR_Я и противо-ЭДС , возникающей в якоре при вращении.

В исполнительных двигателях с независимым возбуждением щетки расположены, как правило, на геометрической нейтрали, поэтому продольная реакция отсутствует. Если к тому же пренебречь влиянием поперечной реакции якоря, то можно считать, что противо-ЭДС якоря

(1.1.2)

где k_ЭМ =kФ – единый электромагнитный коэффициент.

а электромагнитный момент двигателя

(1.1.3)

Дифференциальное уравнение движения вала двигателя имеет вид

(1.1.4)

Предположим, что нагрузка имеет инерционный характер и моментом сопротивления, так же как и моментом трения, можно пренебречь. При разгоне двигателя на холостом ходу () выражение (1.1.4) с учетом (1.1.3) примет вид

(1.1.5)

Подставив в (1.1.1) значения тока из (1.1.5) и ЭДСиз (1.1.2), введя обозначения:- электромеханическая постоянная времени двигателя и- электромагнитная постоянная времени якоря, получим дифференциальное уравнение для угловой скорости вала двигателя:

(1.1.6)

Частное решение этого уравнения представляет собой установившее­ся значение угловой скорости (при равных нулю производных скорости от времени) _уст =U/k_ЭМ. Как правило, в двигателях соблюдается усло­вие 4Тя < Т_м, поэтому корни характеристического квадратного уравне­ния - действительные и разные. В этом случае общее решение однород­ного уравнения имеет вид:

(1.1.7)

где

(1.1.8)

-корни характеристического уравнения ТмT_Яр² + T_мр +1=0.

Решение уравнения (1.1.6) равно, как известно, сумме частного и обще­го решений:

Значения постоянных A₁ и А₂ найдем из начальных условий:

1.  =  _нач в момент t=0;

2. d/dt=0 в момент t=0.

Первое условие означает, что в момент включения вал двигателя неподвижен, второе объясняется тем, что в первый момент вследствие индуктивности якоря ток якоря равен нулю, а следовательно, равен нулю вращающий момент (1.1.3) и ускорение (1.1.5) двигателя.

Подставив начальные условия в (1.1.8) и в производную от (1.1.8) по времени d/dt =₁A₁e^1t+₂A₂e^2t, получим систему уравнений:

₁A₁+₂A₂=0

решая которую, найдем

Подставив значения A₁ и А₂ в (1.1.8), определим окончательное выра­жение для угловой скорости вала двигателя независимого возбуждения при включении якоря под напряжение:

Найдем дифференциальное уравнение для тока якоря в процессе раз­гона вала двигателя. Продифференцировав выражение (1.1.6) и подставив в него из (1.1.5) значения первой, второй и третьей производных от угловой скорости по времени получим дифференциальное уравнение, определяющее изменение тока , во время переходных процессов. При пуске наi-й ступени оно имеет вид:

(1.1.9)

Решение этого уравнения имеет вид:

(1.1.10)

где- корни характеристического уравнения, одинакового для (1.1.6) и (1.1.9). ПостоянныеB₁ и B₂ находим из начальных условий:

1) в моментt=0;

2) U=L_Я(di_Я/dt) в момент t=0.

Первое условие уже объяснялось, второе означает, что в момент включения, когда ток и угловая скорость якоря равны нулю, в левой ча­сти равенства (1.1.1) второе и третье слагаемые также равны нулю, и на­пряжение U уравновешивается только ЭДС самоиндукции якоря.

Подстановка начальных условий в уравнение (1.1.10) и его производ­ную приводит к системе

B₁+B₂=0

₁B₁+₂B₂=U/I_Я

решая которую, находим

Подставив значения B₁ и В₂ в (1.1.10), определим окончательное выра­жение для тока якоря при включении его под напряжение:

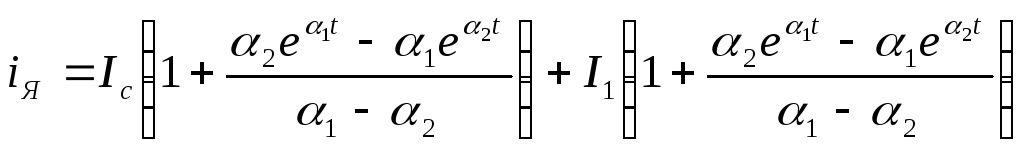
Отметим, что - отрицательны, поэтомуприt, что соответствует идеальному холостому ходу двигателя при M_C=0, когда

Если , то переходной процесс будет колебательным, а функции и i_Я определяются так:

Здесь корни интегрирования получаются комплексно сопряженными и равны:

,