4 Расчет закрытой зубчатой цилиндрической передачи

Вращающий момент на валу шестерни Т₂=118 Н*м при частоте вращения , передаточное числоU₂=5.

Требуемый ресурс передачи (три года при двухсменной работе.). Передача нереверсивная, т.е. работа зубьев одной стороной). Типовой режим нагруженияI (тяжелый). Расположение зубчатых колес относительно опор симметричное.

4.1 Назначение материала шестерни и колеса

Для изготовления зубчатых колес выбираем сталь 45 с термообработкой- улучшение ГОСТ 1054-74 [5, т. 9].

Корпус выполнен из серого чугуна СЧ 18 ГОСТ 1412-70 [5, т. 59]

Принимаем:

для шестерни твердость [4, т. 12.1] при диаметре заготовки

для колеса твердость[4, т. 12.1] в предположении, что наибольшая толщина заготовки колеса

Тогда

4.2 Ориентировочное значение межосевого расстояния находится по формуле при к=10.

Где Т₂- вращающий момент на валу шестерни, U₂-передаточное отношение второй передачи.

4.3 Окружная скорость зубчатого колеса

Где - ориентировочное значение межосевого расстояния;U₂-передаточное отношение второй передачи; n₂- частота вращения вала шестерни

4.4 Допускаемые контактные напряжения:

4.4.1 Интерполированием находим число циклов напряжений, соответствующих перелому кривой усталости(пределу выносливости):

Для шестерни [4, т. 12.8]

Для колеса [4, т. 12.8]

4.4.2 Число циклов нагружения зубьев за все время работы при :

Шестерни :

Колеса

Где n₂- частота вращения вала шестерни; -требуемый ресурс передачи ;U₂-передаточное отношение второй передачи; N_k1- число циклов нагружения зубьев за все время шестерни.

Эквивалентное число циклов нагружения зубьев находим по формуле, значение коэффициента [4, т. 12.2]:

Шестерни:

Колеса

Где N_k1, N_k2- число циклов нагружения зубьев за все время шестерни, колеса.

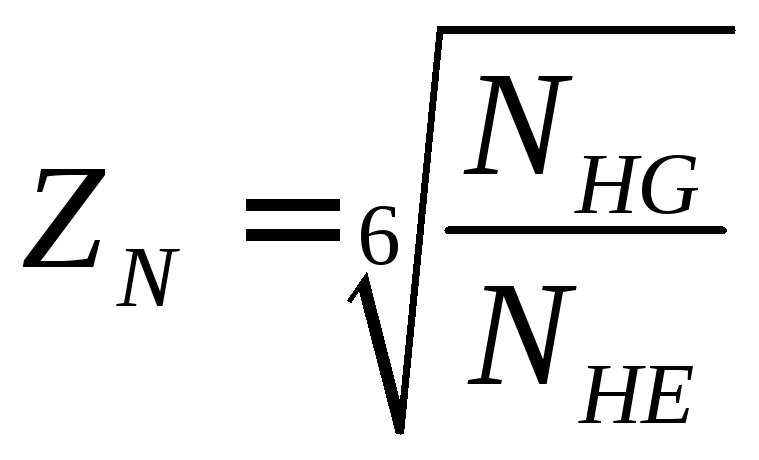4.4.3 Т.к. ,то по условию формулыпри условиипринимаем коэффициент долговечности.

В предположении параметра шероховатости сопряженных поверхностей зубьев с отклонениями профиля неровностей принимаем.

Принимаем значение коэффициента [4, т. 12.9].

Коэффициент запаса прочности для улучшенных колес

4.4.4 Пределы контактной выносливости:

Для шестерни : [4, т. 12.7]

Для колеса [4, т. 12.7]

Где - среднее значение твердости шестерни и колеса.

4.4.5 Допускаемые контактные напряжения

Для шестерни: ;

Для колеса ;

Для расчета прямозубой передачи принимаем меньшее значение: ;

Где - пределы контактной выносливости для шестерни и колеса.

4.5 Допускаемые напряжения изгиба.

4.5.1 Базовое число циклов напряжений соответствует пределу выносливости зубьев при изгибе

4.5.2 Эквивалентное число циклов нагружения зубьев находим по формуле, значение коэффициента [4, т. 12.2], приq_F=6:

Шестерни:

Колеса

Где N_k1, N_k2- число циклов нагружения зубьев за все время шестерни, колеса.

4.5.3 Т.к. ,то по условию формулыпри условиипринимаем коэффициент долговечности.

Полагая шероховатость переходной поверхности между зубьями при зубофрезировании с отклонениями высоты микронеровностей принимаем.

При нереверсивной работе [4, т. 12.9].

Коэффициент запаса прочности

4.5.4 Пределы контактной выносливости зубьев при изгибе :

Для шестерни : [4, т. 12.10]

Для колеса [4, т. 12.10]

Где - среднее значение твердости шестерни и колеса.

4.5.5 Допускаемые напряжения изгиба:

Для шестерни: ;

Для колеса .

4.6 коэффициенты нагрузки

4.6.1 Ориентируясь на передачи общего машиностроения назначаем 8-ю степень точности передач [4, т. 11.2]

Затем интерполированием получаем [4, т.12,5; т. 12.6]

4.6.2 Принимаем коэффициент ширины венца для симметрично расположенных относительно опор колес

По формуле высчитаем коэффициент:

,

Где U₂-передаточное отношение второй передачи.

Выбираем значение коэффициента неравномерностей распределения нагрузки в начальный период работы

Коэффициент К_w находим по таблице для зубчатого колеса (колеса с меньшей твердостью) : К_w=0,38 [4, т. 12.4].

Тогда значения коэффициента после приработки зубьев:

;

Значение коэффициента находим по формуле приG_F=0.91:

4.6.3 Находим значение коэффициента распределения нагрузки между зубьями для назначенной 8-ой степени точности:

4.6.4 Находим значение коэффициентов нагрузки при К_А=1:

4.7 Межосевое расстояние: уточняем межосевое расстояние :

,

Где U₂-передаточное отношение второй передачи; Т₂- момент вращения на валу шестерни; К_Н- коэффициент нагрузки; коэффициент ширины венца для симметрично расположенных относительно опор колес ;-допускаемое контактное напряжение.

Принимаем по ГОСТ а_w=220 мм.

4.8 Ширина венца колеса и шестерни

Где коэффициент ширины венца для симметрично расположенных относительно опор колес;a_w- межосевое расстояние.

4.9 Нормальный модуль зубьев:

Минимальное значение:

мм;

Максимальное значение:

мм;

Где U₂-передаточное отношение второй передачи; Т₂- момент вращения на валу шестерни; a_w- межосевое расстояние; b₂-ширина венца колеса; K_F- коэффициент нагрузки; -допускаемые напряжения изгиба для колеса.

Принимаем m=3 мм [4, т.11.1]

4.10 Число зубьев колес

Суммарное число зубьев:

Число зубьев шестерни и колеса:

Где a_w- межосевое расстояние; U₂-передаточное отношение второй передачи; m- нормальный модуль зубьев.

4.11 Фактическое передаточное число:

Где число зубьев шестерни и колеса.

Для дальнейших расчетов принимаем .

4.12 Проверочный расчет на контактную прочность.

;

Что меньше допускаемого значения . Контактная прочность зубьев обеспечена, поэтому рассчитанные параметры передачи принимают за окончательные.

Где К_Н- коэффициент нагрузки; U₂-передаточное отношение второй передачи; Т₂- момент вращения на валу шестерни; b₂-ширина венца колеса; a_w- межосевое расстояние.

4.13 Сила в зацеплении

Окружная сила:

Где U₂-передаточное отношение второй передачи; Т₂- момент вращения на валу шестерни; a_w- межосевое расстояние.

Радиальная сила: ;

Где F_t- окружная сила.

4.14 Проверочный расчет на прочность при изгибе

Принимаем значения коэффициентов и концентрации напряжений для немодифицированного зацепления(х=0):

Для шестерни: [4, т. 13.1];

Для колеса [4, т. 13.1].

Принимаем расчетные коэффициенты: .

Расчетные напряжения изгиба в основании ножки зуба

Колеса:

шестерни

где b₂-ширина венца колеса; m- нормальный модуль зубьев; K_F- коэффициент нагрузки.

Прочность зубьев обеспечена.

4.15 Основные геометрические размеры передачи

4.15.1 Делительные диаметры шестерни и колеса:

Где m- нормальный модуль зубьев; - число зубьев шестерни и колеса.

4.15.2 Диаметры вершин шестерни и колеса:

Где m- нормальный модуль зубьев; d₁,d₂- делительные диаметры шестерни и колеса.

4.15.3 Диаметры впадин шестерни и колеса

Где m- нормальный модуль зубьев; d₁,d₂- делительные диаметры шестерни и колеса.

4.15.4 Межосевое расстояние

.

4.15.5 Диаметр вала:

;

Где Т₃-крутящий момент на ведомом валу закрытого цилиндрического зубчатого редуктора; - допускаемое напряжение при кручении.

4.16 Дополнительные размеры для цилиндрической передачи.

4.16.1 Диаметр ступицы шестерни

;

Где d_в- диаметр ведущего вала второй передачи.

4.16.2 Длина ступицы

;

Т.к. ,то принимаем.

Где d_в- диаметр ведущего вала второй передачи; b₁-ширина венца шестерни.

4.16.3 Толщина обода цилиндрических колес

; принимаем ;

Где m- нормальный модуль зубьев.

4.16.4 Фаска

.

Где m- нормальный модуль зубьев.

4.17.Выбор соединения с валом по ГОСТ-23360-78

Возьмем соединение шпоночное призматическое. Справочные данные:

Ширина шпонки b [1, т.4.1] 8 мм

Высота шпонки h [1, т.4.1] 7 мм

Глубина паза в валу t₁ [1, т.4.1] 4 мм

Глубина паза во втулку t₂ [1, т.4.1] 3.3 мм

4.17.1 Расчет шпонки на прочность

Шпонка рассчитывается на прочность при смятии:

Шпонка рассчитывается на прочность при смятии: (9), где

l_Р=l_Ш-b (10) и l_Ш=L_ст-10 (11),

где: σ_СМ-напряжение при смятии; d_вала-диаметр вала двигателя; l_Р-рабочая длина шпонки; h-высота шпонки; t₁-глубина паза в валу; l_Ш-длина шпонки;; [σ_см]-допускаемое напряжение при смятии; T₃-крутящий момент на ведомом валу закрытого цилиндрического зубчатого редуктора.

Определим данные: d_вала=29 мм [1, т. 5.1]; [σ_СМ]=60…100 МПа [из лек.];

Подставим известные значения в (11)→(10)→ (9)

по ГОСТ l_Ш=36 мм [примечание к [1, т.4.1]]

l_Р=l_Ш-b=36-8=28 мм;

и < 100 МПа

Найденное значение меньше допустимого