Література

1. ОНД—86. Методика расчета концентраций в атмосферном воздухе вредных веществ, содержащихся в выбросах предприятий. — Л.: Гидрометеоиздат, 1987.

2. Берлянд М.Е., Генихович Е.А., Оникул И.Р. // Тр. ГГО. — Вып. 158 .— 1968. — С. 3 —21.

3. Бызова Н.Л. Методические пособия по расчету рассеяния примеси в пограничном слое атмосферы по метеорологическим данным. — М.: Гидрометеоиздат, 1973.

4. Учет дисперсионных параметров атмосферы при выборе площадок для атомных электростанций. Руководство по безопасности АЭС. — Вена: МАГАТЭ, 1980.

5. Techniques and decision making in the assessment of off-site consequences of an accident in a nuclear facility. Safety series № 86. — Vienne: IAEA, 1987.

6. Гильденскольд Р.С., Недогибченко М.К., Пинигин М.А. Санитарная охрана атмосферного воздуха. — М.: Медицина, 1976

Тема 2 Методика та структура екологічного нормування. Формування державної системи екологічного нормування Практичне заняття 2 (№ зан. 5) Моделі оцінки стану атмосферного повітря

Виявлення тенденцій забруднення навколишнього середовища, як у певний момент часу, так і за період часу, від джерел забруднення приземного шару атмосфери являє собою значний інтерес при рішенні різних проблем, що мають відношення до еколого-гігієнічної безпеки. Тут особливе місце займає завдання прогнозування процесів забруднення атмосфери на певний період попередження. Дослідження фізичних і хімічних процесів у приземному шарі в більшості випадків не дозволяє проводити натурний експеримент. Тому великого значення набуває можливість проведення обчислювального експерименту, для якого необхідна побудова математичних моделей, досить адекватних досліджуваним природним процесам і реалізованих на сучасній обчислювальній техніці. На сьогодні чітко простежується необхідність створення інформаційної системи, одним з компонентів наповнення якої були б дані, отримані в результаті імітаційного моделювання поширення шкідливих речовин в атмосфері в результаті діяльності джерел викидів.

Вихідною інформацією для розробки математичних моделей є оперативна інформація про забруднення (вибірка даних, що представляють собою виміри концентрації забруднюючих речовин у місцях установки контрольно-вимірювальних станцій), метеорологічні параметри (швидкість вітру в приземному шарі, напрямок вітру), а також дані, які визначають структуру поверхні, температуру, фізико-хімічні параметри забруднюючих речовин, різні коефіцієнти.

Існує проблема побудови математичних моделей, що дозволяють досить адекватно описувати поширення домішок. Особливо складно створювати моделі, які могли б моделювати поширення домішок на середні відстані 100-500 км. Для таких моделей потрібне створення спеціальних алгоритмів чисельної реалізації, що дають можливість проводити обчислювальні експерименти одночасно в сотнях тисяч крапок.

Розглянемо один з варіантів побудови математичної моделі поширення домішки в приземному шарі атмосфери.

Завдання розрахунку концентрації q(x,y,z,t) забруднень в атмосфері внаслідок їхнього викиду й переносу можуть бути представлені у вигляді крайового завдання для рівняння [1]:

(1)

де (x₁,x₂,x₃)=(x,y,z) - декартові координати, площина XOY яких відповідає земній поверхні, t - тимчасова координата, (u₁,u₂,u₃) - компоненти поля вітру, - коефіцієнт розпаду речовини, що враховує хімічні перетворення речовини й вимивання його часток опадами, і - коефіцієнти турбулентного переносу, - стала швидкість гравітаційного осідання часток речовини, f=f(x,y,z,t) - відома функція, що описує щільність розподілу джерел забруднення.

Початкові умови звичайно формулюються у вигляді відомої концентрації речовини в досліджуваній області при t=0:

q(x,y,z,0)= q0(x,y,z). (2)

Крайові умови, по-перше, повинні правильно відбивати досліджуваний процес, а по-друге, забезпечувати коректність поставленого завдання. Для рішення розглянутого завдання, область дослідження обмежена, тобто має, наприклад, вид паралелепіпеда: . На бічних границях

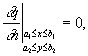(3)

На верхній границі області можливе моделювання різних процесів:

- рівність нулю концентрації речовини:

- відсутність дифузійного переносу за умови, що вертикальна складова швидкості повітря дорівнює нулю:

- наявність потоку речовини через верхню границю:

(4)

Процеси, що відбуваються на поверхні, що підстилає, також можна моделювати різним образом. Наприклад, уважається, що звичайно домішки слабко взаємодіють із поверхнею ґрунту й, потрапивши на неї, не накопичуються, а з турбулентними вихрами знову несуться в атмосферу. Оскільки такі вихри в поверхні невеликі, то можна покласти:

. (5)

Однак при моделюванні таких процесів як формування плям підвищеної концентрації домішки на поверхні, що підстилає, вторинний підйом й осадження часток умова (5) стає незадовільним. Пропонується така умова на поверхні, що підстилає:

(6)

де Q(x,y,t) - концентрація наземного поля домішки, z₀=z*+z, z* - рівень шорсткості, z - товщина шаруючи сальтации. Оскільки ця концентрація може мінятися в часі, то умова (6) доповнюється співвідношенням

(7)

де - швидкість сухого осідання домішки; - інтенсивність вітрового підйому. Використання умов (6), (7) вимагає, у свою чергу, завдання початкової концентрації домішки на поверхні:

Q(x,y,0) = Q₀(x,y). (8)

Якщо поверхня, що підстилає, являє собою дзеркало водного простору, те, припускаючи, що вода поглинає всієї домішки, одержуємо крайову умову

Коректність постановки крайових завдань для рівнянь типу (1) доведена при певних обмеженнях, що накладають на коефіцієнти дифузії й конвекції й для деяких комбінацій крайових умов[3].

Труднощі, що супроводжують реалізацію таких математичних моделей – вибір методу рішення й коректності відповідного різницевого завдання (при застосуванні різницевих методів рішення), забезпечення практичної обчислювальної стійкості алгоритму, необхідність роботи з великими масивами даних. Багато дослідників намагаються вирішити ці проблеми шляхом спрощення моделі, найчастіше за рахунок зменшення розмірності завдання.

Розглянемо математичну модель, що може бути представлена тривимірним крайовим завданням про еволюції наземного поля домішок Q(x,y,t) і поля домішок приземному шарі атмосфери q(x,y,z,t) [2]. Це завдання описується рівнянням (1) при 0, f(x,y,z,t)₀ при заданій початковій концентрації полів домішки (2), (8) і крайових умов (3), (4), (6). Остання крайова умова доповнюється співвідношенням (7). З урахуванням останнього співвідношення завдання про перенос домішки при наявності вітрового підйому й сухого осадження є істотно нестаціонарної, причому динамічна рівновага між концентраціями домішки на поверхні й у приповерхньому шарі виникає через досить тривалий час (t₀ -1), оскільки , згідно [4], досить мале число.

З урахуванням (7) перепишемо крайову умову (6) у вигляді:

або

(9)

Позначивши , перепишемо рівняння (1) у розгорнутому виді:

(10)

Таким чином, за основу математичної моделі обране рівняння (10) з умовами (2) - (4), (8), (9). При побудові чисельного алгоритму для рішення завдання (10), (2) - (4), (8), (9) був використати різницевий метод, запропонований в [4] і була побудована різницева схема, що є монотонної, тобто для неї виконується сітковий аналог принципу максимуму без обмежень на кроки сітки по просторовим змінним. Однієї з особливостей розглянутого завдання являється відсутність модельних прикладів, що дозволяють переконатися в правильності роботи обчислювального алгоритму. У якості однієї зі схем перевірки можна запропонувати наступне. Припустимо, що перенос домішки уздовж однієї з координатних осей, наприклад, уздовж осі OY відсутній, тобто 20, u20. Тоді наше завдання вироджується у двовимірну, для рішення якої розроблені й апробовані надійні алгоритми. Проводячи розрахунки по цих алгоритмах і по запропонованому алгоритмі розрахунку тривимірного завдання й порівнюючи результати, при їхньому збігу з необхідною точністю можна вважати запропонований алгоритм прийнятним.

Програмна реалізація описаного алгоритму була здійснена мовою PASCAL і дозволяє навіть на ЕОМ типу Pentіum з обсягом оперативної пам'яті 32Мб у захищеному режимі вирішувати завдання на сітці розміром до 700 000 вузлів. Алгоритм рішення дозволяє за короткий час одержувати результати чисельного моделювання. При цьому час рахунку залежить як від тимчасового проміжку, протягом якого моделюються процеси, так і від потужності комп'ютера.

Проведено чисельне моделювання для великої кількості варіантів при різних початкових і граничних умов, а також різних значеннях параметрів.

Як приклад розглянемо область (Рис.1), що представляє собою одиничний куб, у початковий момент концентрація домішки нульова, крім крапки (0.136, 0.26, 0.05), де концентрація дорівнює 100.

Поверхня, що підстилає, у початковий момент часу також чиста. Значення інших фізичних параметрів: ; vs =0.4 vd = 0.3; = 0.004; = 0.0; f 0.0; vx = 4.0; vy = 2.0; vz = 0.

Параметри різницевої схеми:. hx = hy = hz = 0.026; = 1/60; = 1.0.

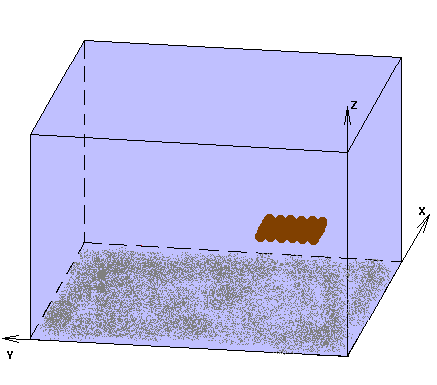
Рис.1.

Рис. 2

Після проведених численних чисельних експериментів, можна говорити про те, що запропонована математична модель, а також алгоритм чисельної реалізації дозволяють ефективно моделювати процеси поширення домішок, і в тому числі на середні відстані.

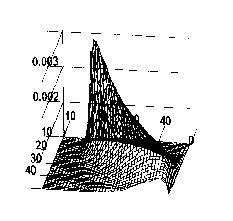
Рис.3

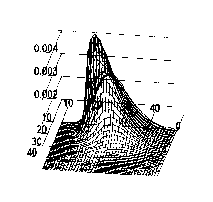
Рис. 4

Таким чином, комп'ютерне моделювання, що базується на запропонованій математичній моделі, дозволяє одержувати інформацію про розподіл домішки в приземному шарі атмосфери від джерел забруднення. При цьому можна одержати інформацію як на майбутнє, при певних початкових даних, так і минулому.

Використовувані засоби графічної візуалізації дозволяють стежити за поширенням домішок у процесі чисельного експерименту, що актуально як при оцінці екстремальних ситуацій, так і при довгостроковому прогнозуванні стану навколишнього середовища.