
- •Методические основы. Определение внутренних сил и напряжений. (сопротивление материалов)
- •Растяжение и сжатие.
- •Растяжение и сжатие.
- •Сдвиговая деформация
- •Поперечный изгиб
- •Сложное сопротивление.
- •Детали машин.
- •Динамика точки и системы.
- •Опоры и направляющие.
- •2. Расчет болта нагруженного поперечной силой и установленного без зазора.
- •3. Расчет резьбы на смятие.
- •Валы и оси
- •Кинематический анализ.
- •Уравнение равновесия системы сил, произвольно расположенных на плоскости.
- •Статика Понятия и определения
- •Аксиомы статики
- •Связи и реакции связи
- •Уравнение равновесия пространственной системы сил
- •1.1. Задачи сопротивления материалов
- •Сопротивление материалов
- •Кинематика
- •Основы динамики точки и тела. Динамика механизмов.
Поперечный изгиб
Чистый изгиб и его особенности
Брусья, работающие на изгиб, называются балками.
Прямым поперечным изгибом называется изгиб, когда внешняя сила перпендикулярна продольной оси балки и проходит через ось симметрии.
(Сила Р вызывает прямой поперечный изгиб, а сила Р1 – косой изгиб).
Косой
изгиб
реализуется, когда силы образуют угол
с плоскостью симметрии величиной
отличающейся от
![]() ,
и проходят через ось балки.
,
и проходят через ось балки.
В поперечных сечениях балки при изгибе возникают два внутренних фактора: поперечные силы и изгибающие моменты.
Если поперечная сила равна нулю, и действует только изгибающий момент, то такой изгиб называют чистым изгибом.
Допущения
Плоские поперечные сечения остаются плоскими и поворачиваются на некоторый равный угол, одно относительно другого, при действии изгибающего момента.
Плоские продольные сечения искривляются.
Слои на вогнутой стороне балки сжимаются, а на выгнутой – растягиваются. Нейтральный слой не изменяет своей длины, а следовательно является ненагруженным.
Определение внутренних силовых факторов.
Внутренние силовые факторы:
- внутренняя сила,
- изгибающий момент,
зависят от внешней нагрузки и изменяются по длине балки.
Для составления уравнений, определяющих значения и , и построения
соответствующих эпюр, принимают следующий правила:
рис.1
Для изгибающих моментов:
Если балка изгибается под действием моментов выпуклостью вниз, то внутренний силовой фактор – момент, действующий в данном сечении балки, принято считать положительным и наоборот; если изгиб происходит выпуклостью вверх, то момент, действующий в сечении балки, будет отрицателен.
Для поперечных сил:
Поперечная сила будет положительна, если внешние силы стремятся приподнять левую часть балки относительно правой, или опустить правую часть балки относительно левой, и наоборот.
Определение значений:
Поперечные силы:
Поперечная сила определяется как алгебраическая сумма сил, расположенных по одну сторону от данного сечения.
Изгибающие моменты:
Изгибающий момент в любом сечении балки равен алгебраической сумме моментов внешних сил, действующих по одну сторону от данного сечения.
q – распределенная сила.
![]()
2) Определение поперечной силы, действующей в сечении х.
![]()
3)Определение изгибающего момента, действующего в сечении х.
![]()
Теорема Журавского (для Рис.3)
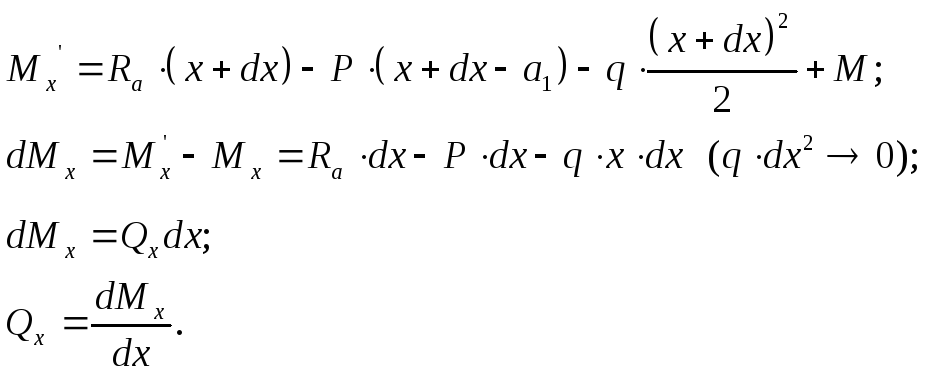 В
соответствии с теоремой Журавского,
поперечная сила является производной
от момента, действующего в сечении, на
расстоянии х.
В
соответствии с теоремой Журавского,
поперечная сила является производной
от момента, действующего в сечении, на
расстоянии х.
Нормальные напряжения при изгибе.
Нормальные напряжения при изгибе вызываются изгибающим моментом, действующим в данном сечении.
В
соответствии с законом Гука
![]() ,
,
Относительное
удлинение при растяжении, которое
реализуется, входе деформации изгиба
-
![]() .
.
Дуга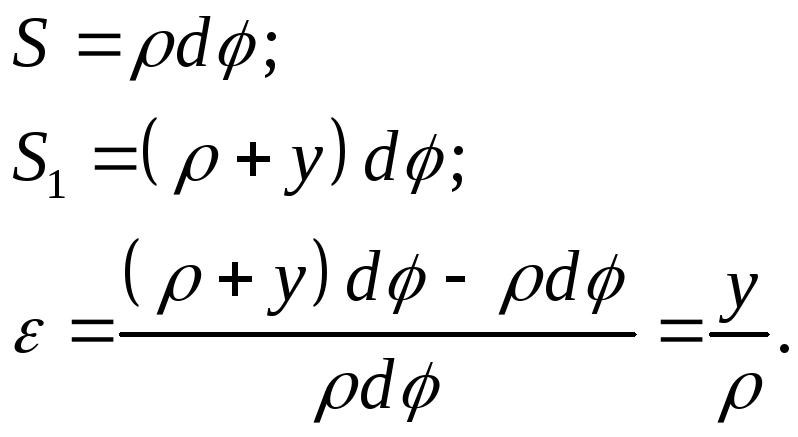
рис.2
Тогда
закон Гука примет вид
![]() .
.
![]()
![]() -
момент инерции относительно нейтральной
оси
-
момент инерции относительно нейтральной
оси
![]()
![]()
![]() если
если
![]()
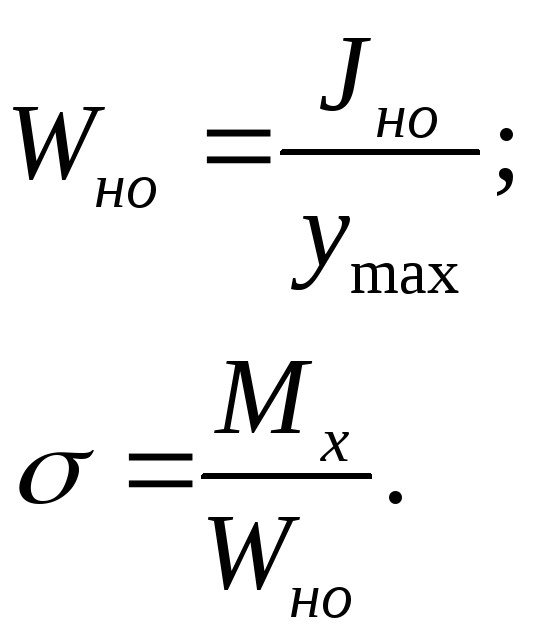
Касательные напряжения при изгибе вызванные действием поперечных сил.
рис.1
![]()
Касательное напряжение - функция статического момента площади.
с учетом (2)
A=b(h/2-y) (3)
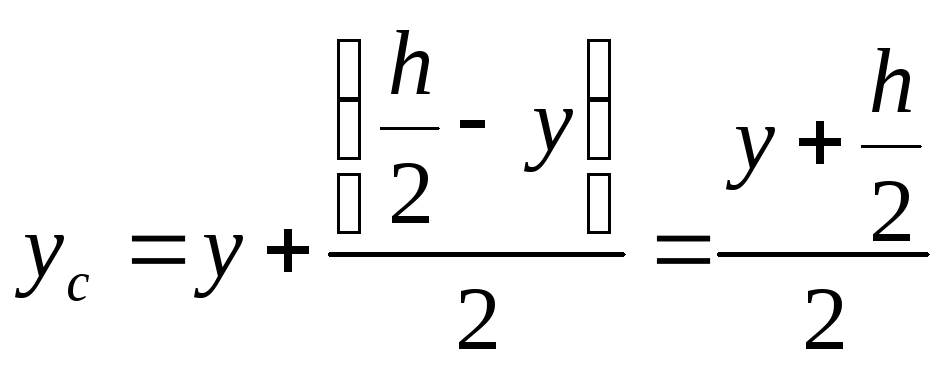 (4)
(4)
с учетом (3) и (4)
![]()
Рассмотрим граничные условия:
При y=h/2 S=0 τ=0
y=-h/2 s=0 τ=0
y=0
![]()
Для сложных форм сечения фигуру разбивают на отдельные части и рассчитывают суммарный статический момент площади поэлементно.
Расчеты на прочность при изгибе
Рассмотрим различные напряженные состояния и возможные условия прочности.
1.
В точках 1 и 4 касательные напряжения
равны нулю, а нормальные напряжения
максимальны и могут быть определены
зависимостью
![]() ≤[σ]
≤[σ]
2. точка 3. Нормальные напряжения равны нулю, касательные напряжения максимальны и определяются уравнением:
![]()
точка 2.
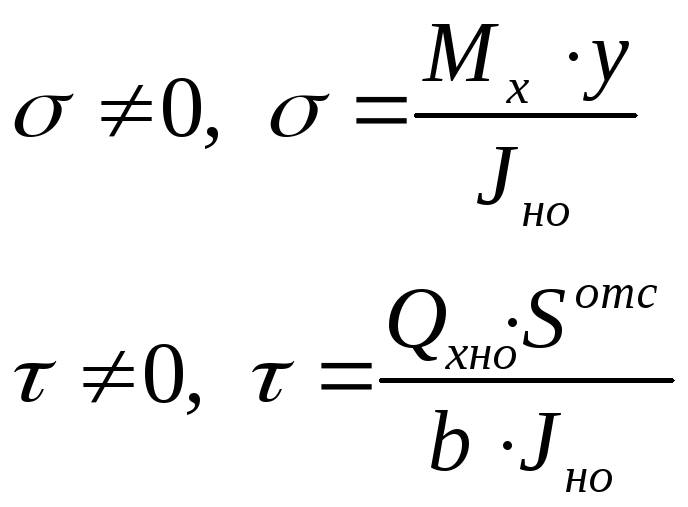
В
соответствии с третьей теорией прочности
![]()
Условие прочности для хрупких материалов:
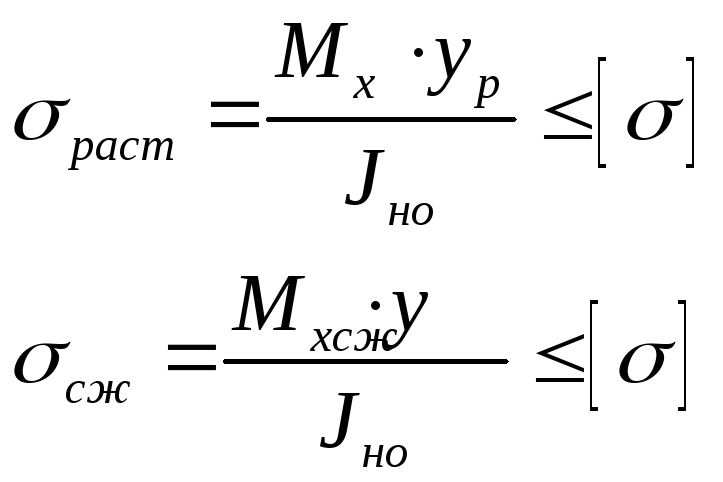 ,
где
,
где
![]() -
расстояние до растягивающихся или
сжимаемых волокон.
-
расстояние до растягивающихся или
сжимаемых волокон.
Б15: Определение перемещений при изгибе.
Перемещения при изгибе. Понятия и определения.
![]()
Прогиб – это перемещение, перпендикулярное исходной оси балки в заданной точке А (у или f).
Угол поворота сечения-α
Имеет место перемещение двух типов:
Линейные (прогиб), и угловые (перемещение перпендикулярно исходной оси балки в заданной точке)
α-определяется положением касательной к точке А1.
Искривленная при повороте ось балки называется упругой линией балки.
Существует несколько методов определения перемещения при изгибе.
Приближенное дифференциальное уравнение упругой линии
![]()
![]()
y’=α – угол наклона.
у=f – прогиб.
![]()
После первого интегрирования получаем выражение для угла поворота сечения.
![]()
Интегрируя повторно, получаем выражение для определения прогиба.
![]()
Постоянные интегрирования находятся из граничных условий (в данном случае опирания балки).
![]()
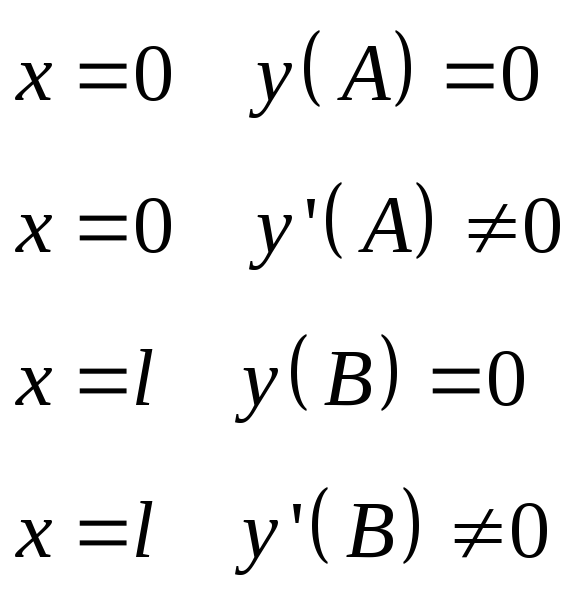
Если
Р посередине, то 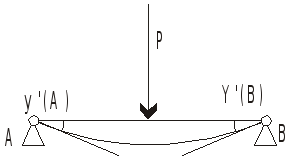
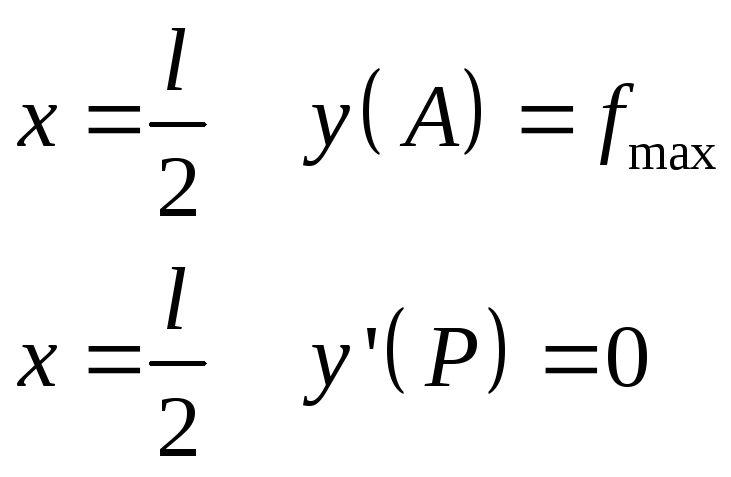
Пример:![]()
За ноль точку А не имеет смысла брать, ввиду того, что в этой точке появляется две реакции – поперечная сила и изгибающий момент.
Если мы идем справа, и за начало принимаем точку В, то момент в сечении х определяется лишь действием распределенной нагрузки Q.
![]()
Тогда
![]()
После интегрирования получаем:
![]()
Нужно получить постоянную интегрирования.
Если
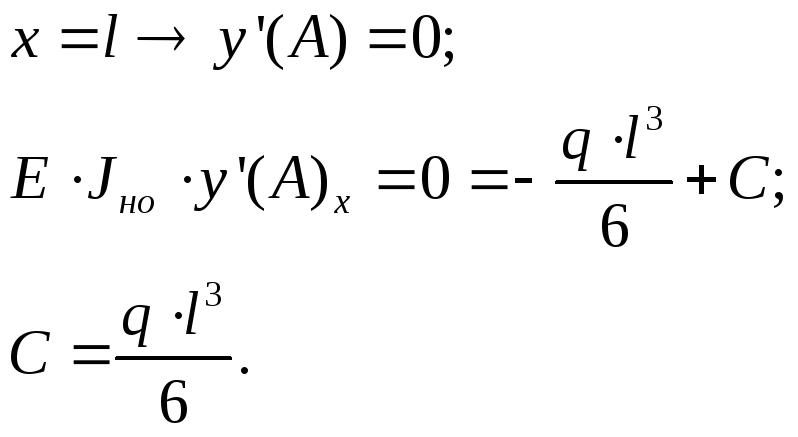
Получаем
![]()
Интегрируя второй раз по аналогии, определяем уравнение для отыскания прогиба, и сам прогиб в точке В.
![]()
при x=l y(0)
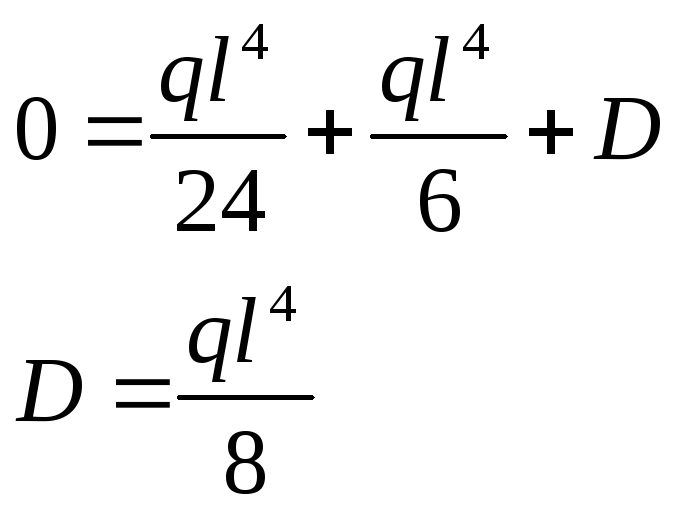
В
итоге
![]()
Универсальное уравнение упругой линии
Для вывода универсального уравнения упругой линии воспользуемся приведенной схемой.
Где:
М – сосредоточенный момент;
Р – сосредоточенная сила;
q – распределенная нагрузка.
![]()
![]()
Интегрируя
выражение 1 с учетом зависимости 2
получаем: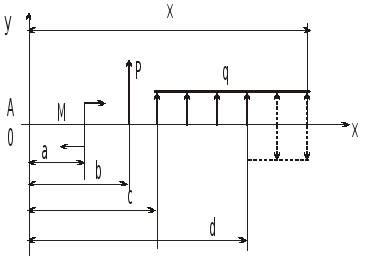
![]()
Интегрируя второй раз получаем:
![]()
При х=0, подставим это в 3 и 4
![]()
![]()
![]()
![]()
Для случая многократного повторения рассмотренных видов нагрузок, универсальные уравнения для определения прогиба и угла поворота в любой точке х принимают следующий вид:
Уравнение для угла поворота в общем виде.
![]()
Уравнение для определения прогиба в общем виде.
![]()
Б16: Сложное сопротивление. Гипотезы прочности. Эквивалентные напряжения.
Б17: Сложное сопротивление. Расчеты на прочность при совместном действии изгиба и кручения.
