Расчет тяги.

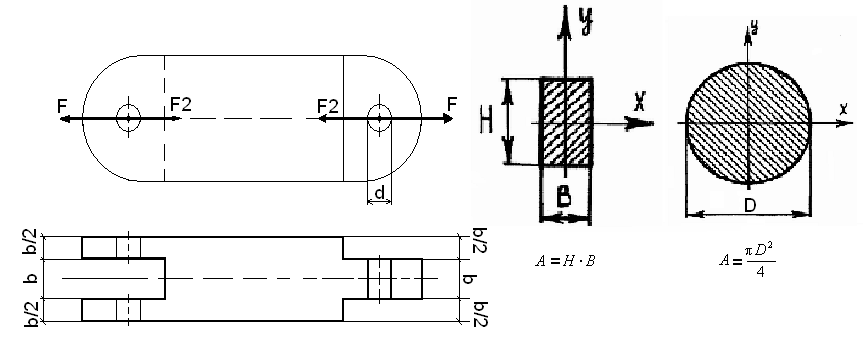
1. К тяге приложено растягивающее усилие F.

Стержень тяге воспринимает продольную нагрузку, под действием которой растягивается. При этом величина абсолютного удлинения определяется по развернутому закону Гука:

σ_р=Eε. ,σ_р=F/A, , σ_р=F/A<=[ σ_р]= σ_T / n -

условие прочности тяги при растяжении, (A=H*B, A=).

Проушины в результате взаимодействия с пальцем сминаются по площади контакта.

Условие прочности при смятии:

σ_см=F/A<=[σ_см]= 2σ_T / n , A=d*b.

Пальцы рассчитываются на срез от взаимодействия с проушинами:

τ_ср=F/A<=[τ_ср]= 0,5σ_T / n; A=*i, i - количество платежей среза (i=2).

2. К тяге приложено сжимающее усилие F2.

Стержень тяги работает на сжатие. Величина абсолютного укорочения определяется так же по закону Гука:

σ_с=F/A<=[σ_с]=[σ_р]=σ_T / n. – Для коротких стержней тяги.

Длинный стержень – когда длина превышает в 3 раза один из размеров поперечного сечения. Здесь существует вероятность мгновенного изгиба стержня тяги.

σ_с=<=[σ_с]=[σ_р]=σ_T / n, φ – коэффициент продольного изгиба, величина табличная – зависит от материала, гибкости стержня и характера закрепления концов стержня.

Проушину и пальцы рассчитывают аналогично предыдущему расчету.

Расчет тонкостенных сосудов.

К тонкостенным сосудам относятся гидро- и пневмо- цилиндры, ресиверы, трубопроводы и т.д.

В зависимости от формы сосуды бывают:

цилиндрические (гидро- и пневмо- цилиндры, некоторые типы ресиверов, трубопроводы);

шаровые (некоторые типы ресиверов, днища и крышки цилиндрических сосудов, мембраны и т.д.);

торовые (криволинейные участки трубопроводов, чувствительные элементы стрелочных манометров).

Во всех сосудах под действием внутренних сил жидкости или газа в стенках возникают напряжения в продольном и поперечном сечении.

Цилиндрические сосуды.

Т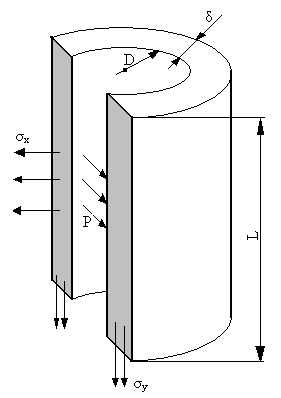онкая цилиндрическая оболочка нагружена внутренним давлением Р.

В стенках сосуда возникают поперечные напряжения σ_x и продольные напряжения σ_y.

Оба напряжения растяжения. Эти напряжения можно определить из условия равновесия рассматриваемой системы.

Условие равновесия: сумма внешних сил, создаваемых давлением Р на соответствующую площадь равна сумме внутренних сил на соответствующих площадях поперечного или продольного сечений.

А) Поперечное сечение:

.

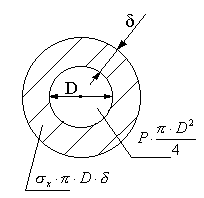
Б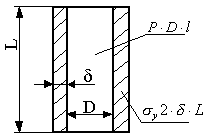) Продольное сечение:

P*D*L=_y2**L .

Шаровые сосуды.

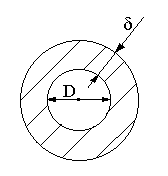- Рассчитываются как поперечное сечение цилиндра.

Торовые сосуды.

Они рассчитываются как искривленные цилиндрические.

15.10.04 Расчет напряжений, возникающих при изменении температуры.

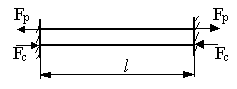
При колебаниях температуры деталь, закрепленная между жесткими опорами, испытывает деформацию сжатия или растяжения. При повышении (понижении) температуры на t стержень должен удлиниться (укоротиться) на величину абсолютного удлинения (укорочения):

l=_t*l*t, где _t – температурный коэффициент линейного расширения (для стали 12*10^-6 С^-1), тогда величина абсолютного удлинения (укорочения): Δε_t= Δl_t / l = α_t*t, но т.к. стержень закреплен жестко, то он не может удлиниться (укоротиться), поэтому в его материале возникнут напряжения сжатия (растяжения), значения которых определяются по закону Гука:

σ_с,р=Е*ε_t=E*α_t*Δt.

На основании закона Гука проводят расчет биметаллических элементов, состоящих из 2-х пластин, спаянных между собой:

^A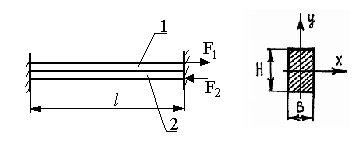₁^=A₂

l₁=l₂=l

Для первой пластины: E₁, α₁, [σ₁]; для второй: E₂, α₂, [σ₂].

Т.к. пластины связаны между собой по всей поверхности, то их линейные деформации должны быть одинаковыми.

Из закона Гука: ε₁=σ₁/Е₁, ε₂=σ₂/Е₂.

При изменении температуры на величину Δt, относительные деформации соответственно изменятся на величину: ε_t1= α₁*Δt; ε_t2= α₂*Δt.

Тогда полная относительная деформация пластин равна:

ε_∑1= ε₁+ ε_t2= σ₁/Е₁+ α₁*Δt

ε_∑2= ε₂+ ε_t2= σ₂/Е₂+ α₂*Δt.

Т.к. ε_∑1= ε_∑2, тогда σ₁/Е₁+ α₁*Δt= σ₂/Е₂+ α₂*Δt.

Напряжения σ₁ и σ₂ эквивалентны следующим силам: F₁= σ₁*A и F₂= σ₂*A, но т.к. биметаллический элемент не подвергается воздействию внешних сил, то условие равновесия системы: F₁=-F₂ . тогда σ₁=-σ₂.

Решая уравнение по абсолютному значению, т.е. σ₁=|σ₂|, получаем:

σ₁/Е₁- σ₂/Е₂= α₂*Δt- α₁*Δt

σ_1,2=(1/Е₁-1/Е₂)= Δt*(α₂- α₁)

σ_1,2=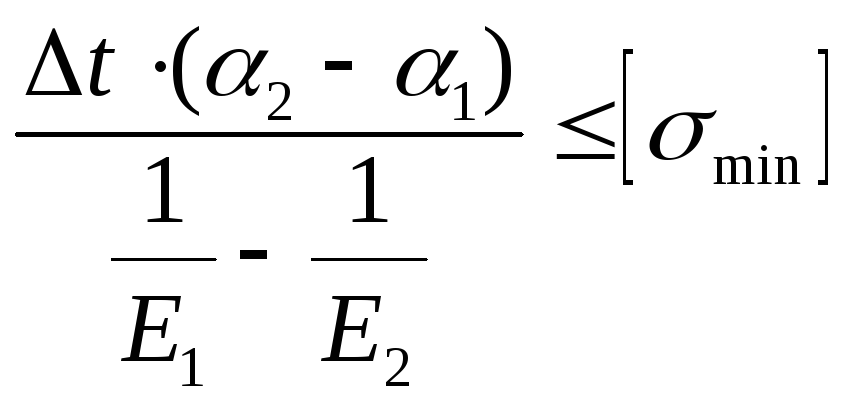- по условию прочности.

При известных марках материалов можно выяснить, на изменение какой температуры работает данный биметаллический элемент, тогда

.
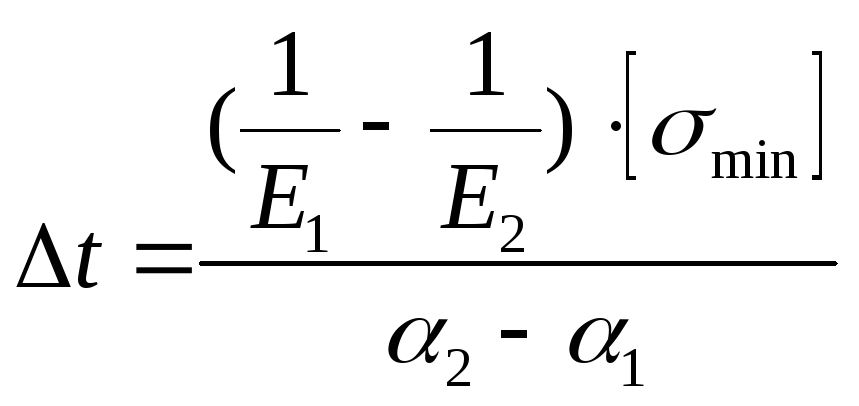