Расчет деталей по коэффициенту запаса прочности.

После расчета деталей на прочность по допускаемым напряжениям проводят расчет на надежность по коэффициенту запаса по прочности. Расчетный коэффициент запаса прочности должен превышать допускаемое значение. n>=[n], где [n] зависит от вида детали, применения и материала.

При одноименных напряжениях, действующих на деталь, соответственно рассчитывают коэффициент запаса прочности по нормальным напряжениям nили по касательным напряжениям

При этом учитывается материал, из которого изготовлена деталь, влияние концентрации напряжений и цикличность нагрузки.

При разноименных напряжениях общий коэффициент запаса прочности находят из зависимости:

>=[n].

(1.10.04) Геометрические характеристики плоских поперечных сечений

При равномерном распределенном напряжении по сечению геометрической характеристикой является площадь поперечного сечения (при деформациях: растяжениях, сжатиях, смятиях, сдвиге, срезе), при неравномерном распределении напряжений геометрическими характеристиками являются осевой момент инерции и осевой момент сопротивления (при деформации изгиба) полярный момент инерции и полярный момент сопротивления (при деформации кручения).

Осевым моментом инерции называется, взятая по всему сечению сумма, произведений элементарных площадок на квадрат расстояния до некоторой оси, лежащей в плоскости рассматриваемого сечения. Величина осевого момента инерции служит характеристикой способности балки сопротивляться деформации изгиба.

J – Осевой момент инерции

J_x=

J_y=

Осевым моментом сопротивления называется отношение осевого момента инерции к расстоянию до наиболее удаленных от нейтральной оси волокон сечения.

W – Осевой момент сопротивления.

W_x = ,W_у =

Полярным моментом инерции называется, взятая по всему сечению, сумма произведений элементарных площадок на квадраты их расстояний до центра тяжести сечения .т.е. до пересечения осей координат.

Полярный момент инерции характеризует способность детали сопротивляться деформации кручения.

- Полярный момент инерции.

= .

Полярным моментом сопротивления называется отношение полярного момента инерции к расстоянию до наиболее удаленных точек сечения от центра тяжести рассматриваемого сечения.

- Полярный момент сопротивления

=.

1. Прямоугольное сечение.

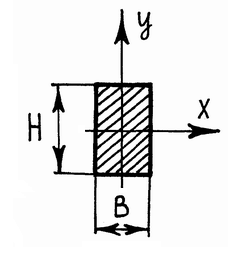
Y=, X=

J_y = (мм⁴), J_x = (мм⁴)

W_x= (мм³), W_y= (мм³)

2. Круглое сечение

x=y=d/2

J_x = J_y = (мм⁴), = (мм⁴)

W_y= W_x= (мм³), = (мм³)

3. Кольцевое сечение

J_x = J_y = - = (мм⁴) , α=d/D

W_y= W_x= (мм³)

= (мм⁴)

= (мм³)

4. Коробчатое сечение.

J_x = =(мм⁴)

J_y = =(мм⁴)

W_x= (мм³)

W_y= (мм³)

Расчеты деталей при равномерном распределении напряжений.

К этому типу деталей относятся тяги с проушинами и пальцами, а так же гидро- и пневмо- цилиндры и другие сосуды, работающие под давлением, биметаллические элементы (термореле).