
- •Рабочая программа, методические указания и контрольные задания
- •Рецензия
- •Пояснительная записка
- •Тематический план для заочной формы обучения
- •Содержание учебной дисциплины
- •Раздел 1. Механика
- •1.1. Кинематика
- •1.2. Динамика
- •1.3. Законы сохранения в механике
- •Раздел 2. Молекулярная физика и термодинамика
- •2.1 Основы мкт
- •2.2 Основы термодинамики
- •2.3 Агрегатные состояния вещества и фазовые переходы
- •Раздел 3. Основы электродинамики
- •3.1. Электрическое поле
- •3.2. Законы постоянного тока
- •3.3 Электрический ток в различных средах
- •3.4. Магнитное поле
- •3.5 Электромагнитной индукции
- •Раздел 4. Колебания и волны
- •4.1 Механические колебания и волны
- •4.2 Электромагнитные колебания и волны
- •Волновая оптика
- •Раздел 5. Квантовая физика
- •5.1 Квантовая оптика
- •5.2. Физика атома и атомного ядра
- •5.3. Термоядерный синтез
- •Раздел 6. Современная научная картина мира
- •Методические указания
- •Контрольные задания контрольная работа №1
- •Контрольная работа №2
- •Самостоятельная работа студентов заочной формы обучения
- •Контрольные вопросы по дисциплине
- •Литература
- •Методические указания к выполнению контрольной работы
- •Содержание
Литература
Основная:
-
Пинский А.А., Граковский Г.Ю. Физика: Учебник / Под общ. ред. Ю.И. Дика, Н.С. Пурышевой. – М.: ФОРУМ: ИНФРА-М, 2005;
-
Смирнов С.А., Глушаков И.Е., Граковскимй Г.Ю. Сборник задач по физике. / Под общ. ред. Смирнова А.В. – М.: ФОРУМ: ИНФРА-М, 2005.
Рекомендуемая:
-
Дмитриева В.Ф. Физика: Учебное пособие для средних спец. учеб. заведений. – М.: Акакдемия, 2007;
-
Энциклопедия элементарной физики: Кн. для учащихся / С.В. Громов. – М.: Просвещение, 2007;
-
Физика для школьников старших классов и поступающих в вузы: учеб. пособие / Б.М. Яворский, А.А. Детлаф. – М.: Дрофа, 2005;
-
Физика. Тесты: Учебно-методическое пособие/Н.К. Гладышева, И.И. Нурминский, А.И. Нурминский и др. – М.: Дрофа, 2003;
-
Самойленко П.И., Сергеев А.В. Физика (учебник для средних спец. учеб, заведений) - Москва: Академия, 2007.
-
Самойленко П.И., Сергеев А.В. Сборник задач и вопросов по физике. – М.: Академия, 2007.
Методические указания к выполнению контрольной работы
Пример 1.
Самолет летел со скоростью 216 км/ч и стал двигаться с ускорением 9 м/с2 в течение 20 секунд. Какое расстояние пролетел самолет за это время и какой скорости он достиг?
|
Дано: υ0 = 216 км/ч а = 9 м/с2 t = 20 с |
СИ 60 м/с |
Решение Движение самолета равноускоренное, ах > 0.
Перемещение
самолета можно определить по формуле:
S
= υ0
t
+ (движение прямолинейное, направление скорости, ускорения и оси Ох совпадают, поэтому индекс «х» в формуле можно не писать). |
|
S - ? υ - ? |
S
= 60 м/с · 20 с +
![]() = 3000 м = 3 км
= 3000 м = 3 км
Конечную скорость самолета можно определить по формуле:
υ = υ0 + аt
υ = 60 м/с + 9 м/с2 · 20 с = 240 м/с.
Ответ: S = 3 км; υ = 240 м/с.
Пример 2.
Определите модуль скорости и центростремительного ускорения точек земной поверхности на экваторе. Радиус Земли принять равным 6400 км.
|
Дано: R = 6400 км Т=24ч |
СИ 6,4 • 106 м 8,64·104с |
Решение Точки земной поверхности на экваторе движутся по окружности радиуса R, поэтому модуль их скорости
|
|
|
υ
=
![]() = 4,65 · 102
м/с = 465 м/с.
= 4,65 · 102
м/с = 465 м/с.
Центростремительное ускорение можно найти:
![]()
ацс
=
![]() = 3,4 · 10-2
м/с2
= 3,4 · 10-2
м/с2
![]()
Пример 3.
Шар массой m1, движущийся горизонтально с некоторой скоростью 1, столкнулся с неподвижным шаром массой m2. Шары абсолютно упругие, удар прямой, центральный. Какую долю своей кинетической энергии первый шар передал второму?
|
Дано: m1 1 m2 |
Решение Доля энергии, переданной первым шаром второму, выразится соотношением
|
|
= ? |
где Т1 - кинетическая энергия первого шара до удара; u2 и Т2 - скорость и кинетическая энергия второго шара после удара.
Как видно из формулы, для определения надо найти u2 закона сохранения: 1) закон сохранения импульса и 2) закон сохранения механической энергии. Пользуясь этими законами, найдём u2. По закону сохранения импульса, учитывая, что второй шар до удара покоился, получим
![]() .
.
По закону сохранения механической энергии
![]() .
.
Решая совместно эти два уравнения, найдём
 .
=>
.
=>
 .
.
Из полученного соотношения видно, что доля переданной энергии зависит только от масс сталкивающихся шаров. Доля передаваемой энергии не изменится, если шары поменяются местами.
Ответ:
=
![]()
Пример 4.
Парашютист раскрывает парашют спустя 2 с после отделения от самолета. Какое расстояние он проходит по вертикали и какова конечная скорость в конце этого промежутка времени?
|
Дано: υ0= 0 t =2 с g = 10 м/с2 у0 = 0 |
Р Направим ось Оу вертикально вниз, началом отсчета будем считать момент отделения парашютиста от самолета. Тогда уравнение движения парашютиста имеет вид:
|
|
S - ? υ - ? |
с учетом направления оси Оу и векторов скорости и ускорения свободного падения.
По условию v0 = 0 и у0 = 0. Следовательно, перемещение парашютиста по вертикали:
![]()
S
=
![]() = 20 м.
= 20 м.
Скорость в конце 2 с движения найдем по формуле:
![]() =>
=>![]()
υ = 10 м/с2 · 2 с = 20 м/с.
![]()
Пример 5.
Лыжник массой 50 кг движется со скоростью 20 м/с по вогнутому, а затем выпуклому участкам дороги с радиусом кривизны 20 м. Определить вес лыжника в средней точке каждого участка.
|
Дано: т = 50 кг; υ = 20 м/с; R = 80 м; g = 9,8 м/с2
|
Решение Движение лыжника по выпуклому и вогнутому участкам дороги можно рассматривать как движение по дуге окружности. Систему отсчета свяжем с-Землей, выберем прямоугольную систему координат хОу. Ось у направим к центру окружности, а ось х — по касательной к ней.
|
|
Р1 - ? Р2 - ? |
За начало отсчета можно принять точку, в которой в данный момент находится лыжник, — среднюю точку каждого участка.
В
обоих случаях на лыжника действует сила
тяжести F=
mg
и сила реакции опоры N.
Для описания движения запишем второй
закон Ньютона в векторной форме:
![]() Движение
с центростремительным ускорением.
Движение
с центростремительным ускорением.
1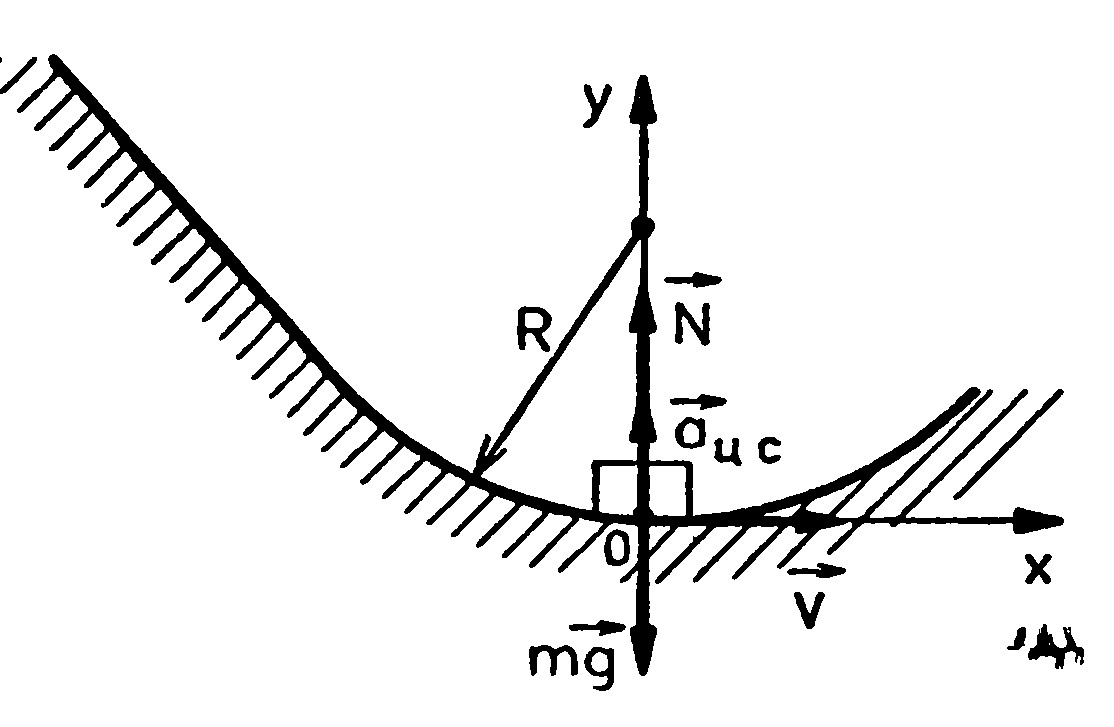 )
На вогнутом участке дороги. ускорение
лыжника направлено к центру окружности
по радиусу и направление вектора
)
На вогнутом участке дороги. ускорение
лыжника направлено к центру окружности
по радиусу и направление вектора
![]() совпадает с направлением оси у.
В проекциях на ось у
второй закон Ньютона имеет вид: Оу: N
– mg = maцс
=> N = mg + maцс
= m(g + aцс)
совпадает с направлением оси у.
В проекциях на ось у
второй закон Ньютона имеет вид: Оу: N
– mg = maцс
=> N = mg + maцс
= m(g + aцс)
Центростремительное ускорение находят по формуле
![]() =>
N = m(g +
=>
N = m(g +
![]() ).
).
По
третьему закону Ньютона модуль силы
реакции опоры равен весу лыжника, то
есть
![]() =
=![]() => Р1
= m(g +
=> Р1
= m(g +
![]() ).
).
Р1
= 50 кг (9,8 м/с2
+
![]() )
= 740 Н.
)
= 740 Н.
2 )
На выпуклом участке дороги ускорение
лыжника также направлено к центру
окружности по радиусу, но направление
вектора ускорения противоположно оси
у, поэтому его проекция на ось у, будет
отрицательна. Второй закон Ньютона в
проекциях на ось у имеет вид:
)
На выпуклом участке дороги ускорение
лыжника также направлено к центру
окружности по радиусу, но направление
вектора ускорения противоположно оси
у, поэтому его проекция на ось у, будет
отрицательна. Второй закон Ньютона в
проекциях на ось у имеет вид:
Оу:
N – mg = – maцс
=> N = mg – maцс
= m(g – aцс)
=> N = m(g –
![]() ).
).
По
третьему закону Ньютона:
![]() =
=![]() => Р2
= m(g –
=> Р2
= m(g –
![]() ).
).
Р2
= 50 кг (9,8 м/с2
–
![]() )
= 240 Н.
)
= 240 Н.
Ответ: Р1 = 740 Н, Р2 = 240 Н.
Пример 6.
Автомобиль массой 5 т движется с постоянной скоростью по прямой горизонтальной дороге. Коэффициент трения шин о дорогу равен 0,03. Определите силу тяги, развиваемую двигателем.
|
Дано: т = 5т μ = 0,03 υ = const g = 9,8м/с2 |
СИ 5 • 103 кг |
Р На автомобиль действуют четыре силы: сила тяги, сила трения, сила тяжести и сила реакции опоры (дороги). |
|
Fтяг = ? |
Для описания движения выберем прямоугольную систему координат 0ху. Применяя второй закон Ньютона, получим:
![]()
В проекциях на оси:
0х: 0 + Fт + 0 – Fтр = 0, при υ = const
0у: N + 0 – mg + 0 = 0
=> N = mg, Fт = Fтр => Fтр = μ N = μ mg => Fт = μ mg
Fт = 0,03 · 5 · 103 кг · 9,8 м/с2 = 1470 Н.
Ответ: Fт = 1470 Н.
Пример 7.
Груз массой 0,4 кг, подвешенный к невесомой пружине, совершает 30 колебаний в минуту. Чему равна жесткость пружины?
|
Дано: m = 0,5 кг N = 20 t = 1 мин |
СИ
60 с |
Решение
Период
колебаний математического маятника
Т = 2π
зависит от длины нити и ускорения свободного падения.
Период
колебаний: Т =
|
|
k = ? |
=>
![]() = 4π2
= 4π2
![]() =>
k
=
=>
k
=
![]()
k
=
![]() =
2,2 Н/м
=
2,2 Н/м
Ответ: k = 2,2 Н/м
Пример 8.
Предельно допустимая концентрация молекул паров ртути в воздухе равна 3· 1016 м-3. При какой массе паров ртути в одном кубическом метре воздуха появляется опасность отравления?
|
Дано: n = 3•1016 м-3 V= 1 м3 μ= 201 • 10-3 кг/моль NA = 6,02 • 1023 моль-1 |
Решение
Концентрация
частиц: n
=
Массу
паров ртути можно определить: m = ν ·
μ =
Число
частиц: N
= n
· V
=> m
=
|
|
m = ? |
m
=
![]() = 10-8
кг
= 10-8
кг
Ответ: m = 10-8 кг
Пример 9.
В сосуде находится газ. Какое давление он производит на стенки сосуда, если масса газа 5 г, его объем 1 л, средняя квадратичная скорость молекул 500 м/с?
|
Дано: m = 10 г V = 2 л
|
СИ 10 · 10-3 кг 2 · 10-3 м3 60 с |
Решение
Используем
основное уравнение МКТ идеального
газа: р =
р
=
|
|
р = ? |
р
=
![]()
![]() ≈ 4,2
· 105
Па
≈ 4,2
· 105
Па
Ответ: р = 4,2 · 105 Па.
Пример 10.
В сосуде вместимостью 500 см3 содержится 0,89 г водорода при температуре 17°С. Определите давление газа.
|
Дано: m = 1 г V = 500 см3 t = 17 °С R = 8,31Дж/моль · К μ = 2 • 10-3 кг/моль |
СИ 1 · 10-3 кг 5 · 10-4 м3 290 К |
Решение Воспользуемся уравнением Менделеева-Клапейрона:
рV
=
р
=
|
|
р = ? |
Ответ: р = 2,4 МПа
Пример 11.
Воздух под поршнем насоса имел давление 10 Па и объем 200 см3. При каком давлении этот воздух займет объем 130 см3, если его температура не изменится?
|
Дано: m = const V1 = 300 см3 V1 = 150 см3 Р1 = 105 Па Т1 = Т2 = const |
СИ
3 · 10-4 м3 1,5 · 10-4 м3
|
Решение Этот процесс можно рассматривать как изотермический. По закону Бойля-Мариотта::
р1V1
= р2
V2
=> р2
=
р2
=
|
|
Р2 = ? |
Ответ: р2 = 2 · 105 Па
Пример 12.
С какой силой взаимодействуют два заряда по 1 Кл каждый на расстоянии 1 км друг от друга в вакууме?
|
Дано: q1 = q2 = 1Кл r = 1 км k = 9·109Н·м2/Кл2 |
СИ
10-3 м
|
Решение
С
закону
Кулона: F
= k |
|
F = ? |
F
= 9 · 109
Н·м2/Кл2![]() = 9 · 103
Н = 9 кН
= 9 · 103
Н = 9 кН
Заряды
отталкиваются, так как одноименные
заряды отталкиваются, сила
![]() = -
= -![]() ,
то есть сила, с которой заряд q1
действует на заряд q2,
равна по модулю и противоположна
по направлению силе, с которой заряд q2
действует на заряд q1.
,
то есть сила, с которой заряд q1
действует на заряд q2,
равна по модулю и противоположна
по направлению силе, с которой заряд q2
действует на заряд q1.
Ответ: F = 9 кН.
Пример 13.
Чему равно сопротивление участка цепи, состоящего из трех резисторов сопротивлением по 4 Ом каждый, если они соединены 1) последовательно, 2) параллельно?
|
Дано: R1 = R2 = R3 = 4 Ом |
Р 1) Полное сопротивление участка при последовательном |
|
Rоб = ? |
соединении: Rоб = R1 + R2 + R3
R об
= 3 · 4 Ом
= 12 Ом.
об
= 3 · 4 Ом
= 12 Ом.
2) Полное сопротивление участка при параллельном соединении можно рассчитать, зная, что:
![]() =
=
![]() +
+
![]() +
+
![]() =
=
![]() => Rоб
=
=> Rоб
=
![]()
Rоб
=
![]() = 1,7 Ом
= 1,7 Ом
Ответ: Rоб = 12 Ом; Rоб = 1,7 Ом.
Пример 14.
На дифракционную решетку в направлении нормали к её поверхности падает монохроматический свет. Период решётки d=2 мкм. Какого наибольшего порядка дифракционный максимум даёт эта решётка в случае красного света (1=0,7 мкм) и в случае фиолетового (2=0,41 мкм)?
|
Дано: d=2 мкм 1=0,7 мкм 2=0,41 мкм |
СИ 2 · 10-6 м 0,7 · 10-6 м 0,41 · 10-6 м
|
Решение На основании формулы дифракционной решётки запишем следующее выражение порядка дифракционного максимума:
|
|
т = ? |
Т![]() ак
как sin
не может
быть больше 1, то число m
не может быть больше d/l,
то есть
ак
как sin
не может
быть больше 1, то число m
не может быть больше d/l,
то есть
=>
для
красных лучей m ≤![]() = 2,86,
= 2,86,
для
фиолетовых лучей m ≤![]() = 4,88.
= 4,88.
Если учесть, что порядок максимумов является целым числом, то найдём, что для красного света mмакс=2 и для фиолетового mмакс=4.
Ответ: красного света mмакс=2, для фиолетового mмакс=4.
Пример 15.
Вычислить дефект массы и энергию связи ядра 3Li7 .
|
Дано: 3Li7 |
Решение Дефект массы ядра ( m ) – разность между суммой масс свободных нуклонов (протонов и нейтронов) и массой ядра, т.е. ∆m = Z· mp + N· mn – Mя; |
|
∆т= ? Есв = ? |
Mя = Mа – Z · mе =>
=> ∆m = Z· mp + N· mn – (Mа – Z · mе ) = Z· (mp + mе) + N· mn – Mа,
где mp + mе = MН,
MH – масса атома водорода, окончательно найдём
∆m = Z· MH + N· mn – Mа
∆m = 3· 1,00783 а.е.м. + 4 · 1,00876 а.е.м. – 7,01601 а.е.м. = 0,04216 а.е.м.
В соответствии с законом пропорциональности массы и энергии:
Eсв = ∆mc2
Eсв = 0,04216 а.е.м · 931 МэВ/а.е.м. = 39,2 МэВ
Ответ: ∆m =0,04216 а.е.м.; Eсв = 39,2 МэВ.


 ешение
ешение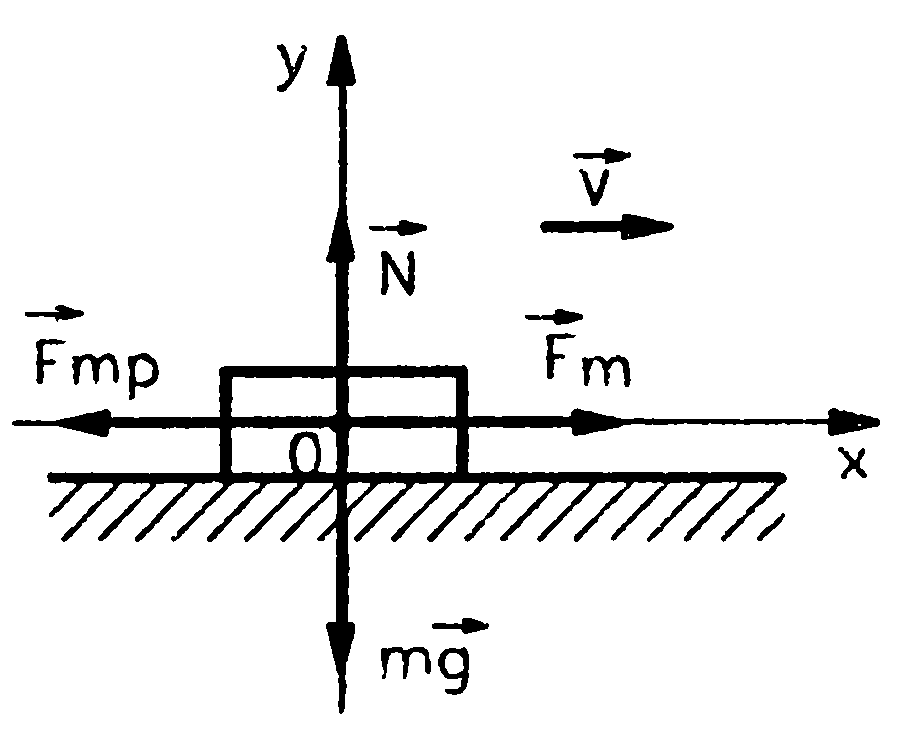 ешение
ешение