3 Статистический анализ результатов экспериментов

Под статистикой здесь и далее будет подразумеваться фиксация конкретных результатов различных случайных явлений и экспериментов.

n

Рассмотрим более детально эксперимент с бросанием монеты n раз. Результат каждого отдельного испытания очевидно непредсказуем и имеет всего два исхода ‘’орел’’ или ’’решка’’. Обозначим символом m количество выпадений орла в результате эксперимента. Число m называется частотой данного случайного события, а величина р= - его относительной частотой. Реально проводимый эксперимент с неизбежностью убеждает, что относительная частота выпадений орла с увеличением числа испытаний стабилизируется около 1/2 , т.е. примерно в половине испытаний выпадает орел и величина эта тем ближе к 0,5 чем больше количество испытаний. На изображенном ниже рисунке принцип

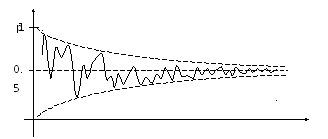
стабилизации относительной частоты реализуется как размещение ее графика при наличии хаотичности в канале между двумя кривыми, асимптотически приближающимися к горизонтальной прямой р=0,5 .

Подводя выше изложенному итог, зафиксируем основные особенности случайного эксперимента:

 непредсказуемость исхода отдельного испытания;

 возможность неограниченного повторения испытаний в одинако-

вых условиях;

 стабилизация относительной частоты случайного события с увели-

чением количества испытаний.

Величина, около которой происходит стабилизация относительной частоты случайного события как раз и характеризует его вероятность. Нередко в свой речи мы выражаем интуитивное понимание вероятности реализации той или иной ситуации формулировками типа “шансы пятьдесят на пятьдесят” или “девять против одного”. Теория вероятностей поднимает тему случайности до уровня серьезной и строгой науки.

4 Множество событий и операции на нем

В каждом конкретном случайном эксперименте случайные события образуют множество, на котором могут быть введены различные операции, позволяющие из простейших событий формировать сложные события. В дальнейшем, следуя традиции, случайные события как элементы соответствующего множества будут обозначаться прописными латинскими буквами, а когда это будет удобно, то и русскими. Словесное описание содержания события раскрывается с помощью знака равенства, который в данной ситуации читается как “состоит в том, что”. Например, запись А=“выпал орел” может быть прочитана как написано и означает, что содержанием события А является выпадение орла при бросании монеты.

Первой в списке операций логично поставить сравнение событий.

Если событие В происходит всегда, когда произошло событие А, то говорят что из А следует В и эту ситуацию обозначают символом АВ.

Например, если при бросании кубика А=”выпала цифра 2’’ и В=”выпало четное число”, то АВ. Однако в данной ситуации очевидно из В не следует А, т.е. ВА. Таким образом все случайные события относительно друг друга находятся в отношении следствия с ответом “да” или “нет”.

Первичным элементом математических операций является равенство.

События А и В называются равными, если из А следует В и наоборот, т.е. АВ и ВА  А=В. Например, если при бросании кубика А=”выпало четное число”, а В=”выпало или 2 или 4 или 6”, то А=В.

Суммой двух событий называется событие А+В, которое состоит в том, что произошло событие или А или В или оба одновременно. Здесь “одновременно” не просто слово, а термин, понимаемый не буквально как реализация событий физически в один момент времени, а в смысле “вместе”. В этом определении “или” имеет не исключающий характер, поскольку допускает совместное возникновение событий. Если в эксперименте со стрельбой =”попасть в мишень в первом выстреле”, а =”попасть в мишень во втором выстреле”, то +=”попасть или в первом выстреле или во втором выстреле или попасть одновременно в первом и втором выстреле, т.е. дважды”, что означает в серии из двух выстрелов попасть хотя бы один раз. Таким образом, рассматривается одновременное (в смысле вместе) попадание в двух выстрелах, хотя одновременно произвести два выстрела из одного и того же оружия принципиально невозможно.

Применение к случайным событиям символики теории множеств объясняется глубоким идейным сходством таких объектов как множества и случайные события. Поэтому аналогично теории множеств в теории вероятностей операции над случайными с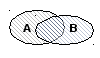обытиями иллюстрируются кругами Эйлера. Сумма событий является аналогом объединения множеств и обозначается соответственно как заштрихованная область.

Из определения суммы событий следует, что она обладает свойствами коммутативности (перестановочности слагаемых)

А+В=В+А

и ассоциативности (изменения порядка суммирования)

А+(В+С)=(А+В)+С.

Очевидно, что АА+В В, а также А+А=А. Последний результат свидетельствует о принципиальном отличии алгебры событий от привычной алгебры чисел.

Упражнение. При бросании кубика представить случайное событие А=”выпало четное число” в виде суммы событий его составляющих, введя соответствующие обозначения.

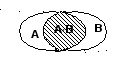Произведением двух событий А и В называется событие АВ или просто АВ, которое заключается в том, что события А и В произошли одновременно. Геометрическая интерпретация этой операции выглядит аналогично пересечению множеств как общая часть обоих эллипсов. Применительно к задаче о двух выстрелах по мишени при обозначении = “попадание в первом выстреле”, а =”попадание во втором выстреле” попадание дважды будет являться произведением этих событий, т.е. =”попасть дважды”.

Умножение событий коммутативно (сомножители можно менять местами)

АВ= ВА,

ассоциативно (сомножители можно группировать в указанном порядке)

А(ВС)=(АВ)С

и дистрибутивно (можно раскрывать скобки и выносить общий множитель за скобки)

А(В+С)=АВ+АС.

Скобки, как и обычно, устанавливают приоритет операций.

Рассмотренные операции над событиями в частности имеют своими следствиями: А АВВ, (А+В)(А+С)=АА+АС+ВА+ВС=А+АС+АВ+ВС=(А+АВ)+АС+ВС=А+АС+ВС=(А+АС)+ВС===А+ВС. Здесь учтено то обстоятельство, что А+АВ=А при любом В как сумма события фактически с самим собой, в чем нетрудно убедиться с помощью кругов Эйлера.

Упражнение. Доказать последнее свойство непосредственно с помощью кругов Эйлера для всех трех событий А, В и С.

Основное назначение операций над событиями  формирование из простых событий более сложных.

Примеры.

1. В серии из пяти выстрелов по мишени событие С=”не менее 3-х попаданий” представимо в виде суммы событий С=, где =”ровно ‘к’ попаданий”.

2. При одновременном бросании двух кубиков событие С=”сумма выпавших цифр четна” реализуется в случае четности или нечетности обеих цифр и потому С= , где =”на 𝑖-м кубике выпало четное число”, а =”на 𝑖-м кубике выпало нечетное число”.

Событие называется противоположным событию А, если оно состоит в том, что А не произошло (А=”выпал орел”  =”выпала решка”).

Событие Ω называется достоверным, если оно происходит всегда (“выпал орел или решка”=Ω).

Событие ∅ называется невозможным, если оно не происходит никогда (“выпал орел и решка”=∅).

События А и В называются несовместными, если они не могут произойти одновременно. Для несовместных событий А и В очевидно АВ=∅, т.е. произведение двух несовместных событий  невозможное событие.

Событие (исход) называется элементарным, если оно неразложимо в сумму других событий.

События образуют полный набор, если они все попарно несовместны, т.е. =∅ при  𝑖≠𝑗, а их сумма  достоверное событие =Ω . В примере с бросанием кубика, обозначив =”выпала цифра ‘𝑖’ ”, получаем шесть попарно несовместных элементарных событий, которые в своей сумме очевидно дают достоверное событие. Таким образом события , образуют полный набор (аналог базиса в векторной алгебре) и любое сложное событие будет представлять собой некоторую комбинацию этих элементарных исходов.

Из выше изложенного следует, что =∅, =Ω, А+=Ω, А=∅ ввиду несовместности события с ему противоположным. Таким образом, событие и ему противоположное образуют полный набор.