Последовательность выполнения работы

Данная работа выполняется на листе чертежной бумаги форматом А2 (420х594). Работа выполняется по вариан-там (см. «Задание.Doc»).

Строятся координатные оси и горизонтальные и фрон-тальные проекции точек. Затем, в соответствии со спосо-бом задания плоскостей, строятся плоскости (Их части, ог-раниченные заданными точками).

Рассмотрим последовательность построения линии пере-сечения плоскостей в ортогональных проекциях для нес-кольких вариантов.

Построение линии пересечения плоскостей в случае, когда они заданы треугольниками АВС и DEF, рассмот-рено на рис.9 и рис.10. На рис.9 точки К₁ и К₂ линии пер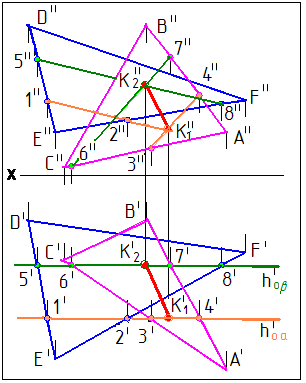есечения определяются

с помощью вспомогательных секущих плоскостей  и β ( и β- фронтальные плоскости).

Алгоритм решения:

1.  || П₂

2. (1,2)=  ∩ γ(ΔDEF)

/\ (3,4)=  ∩ Σ(ΔАВС)

3. К₁ = (1,2) ∩ (DE)

4. β || П₂ Рис. 9

5. (5,6)= β ∩ γ(ΔDEF)

/\ (7,8)= β ∩ Σ(ΔАВС)

6. К₂ = (5,6) ∩ (7,8)

7. (К₁К₂) = Σ(ΔАВС) ∩ γ(ΔDEF)

На рис. 10 линия пересечения плоскостей, заданных треугольниками АВС и DEF, определяется по секущим плоскостям, которые проводятся через уже существующие стороны (это уменьшает колличество вспомогательных точек).

Заключим прямую EF во вспомогательную плоскость

(фронтально-проецирующую плоскость ). 1^II 2^II - фронтальная проекция линии пересечения плоскости  и плоскости Σ, заданной треугольником АВС. Определяем горизонтальные проекции 1^I и 2^I. При пересечении 1^I 2^I с горизонтальной проекцией прямой Е^IF^I получаем горизонтальную проекцию К₁^I. Проекцию К₁^II находим на Е^IIF^II. Вторая точка, принадлежащая линии пересечения плоскостей, находится аналогично. Заключаем прямую АС в горизонтально - проецирующую плоскость β. 3^I 4^I - горизонтальная проекция линии пересечения плоскости β с плоскостью γ, заданной треугольником DEF. Пересечение 3^II 4^II с фронтальной проекцией прямой АС дает фронтальную проекцию точки К₂^II. Проекцию К₁^I ищем на соответствующей проекции прямой. К₁ К₂ - линия пересечения плоскостей.

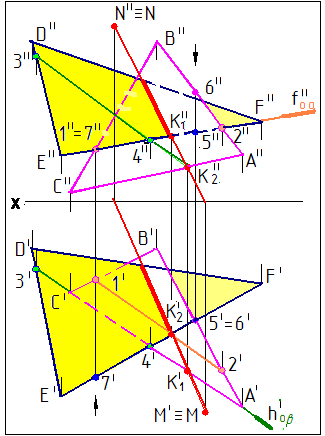
Алгоритм решения задачи (Рис 10):

1.  Э (EF) /\  ┴ П₂

2. (1,2) =  ∩ Σ(ΔАВС)

3. К₁ = (1,2) ∩ (EF)

4. β Э (AC) /\ β ┴ П₂

5. (3,4) = Ф ∩ γ(ΔDEF) Рис.10

6. К₂ = (3,4) ∩ (AC)

7. (К₁К₂) = Σ(ΔАВС) ∩ γ(ΔDEF)

Видимость плоскостей определяется с помощью метода конкурирующих точек, сущность которого была рассмот-рена выше.

Пример определения линии пересечения плоскостей для случая, когда одна из плоскостей задана следами h_oγ^I и f_oγ^II.

На рис. 11 линия пересечения плоскостей К₁ К₂ определена с помощью вспомогательных секущих плоскостей  и β (Горизонтальные плоскости).

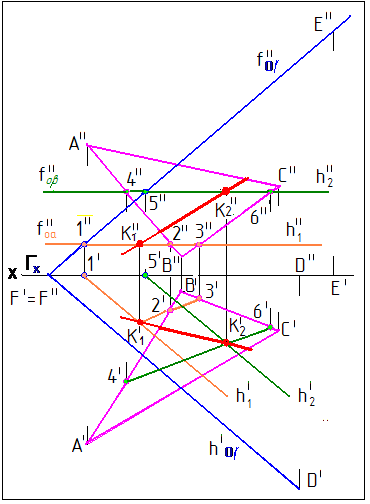
Рис. 11

Вспомогательная плоскость  пересекает плоскость Σ, заданную треугольником АВС, по прямой (2,3). 2^II 3^II- фрон-тальная проекция этой линии пересечения. Плоскость  пересекает плоскость γ, заданную следами, по горизон-тальной прямой h₁, проходящей через точку 1. Пересечение горизонтальных проекций 2^I 3^I и h₁^I дает горизонтальную проекцию точки К₁^I. Фронтальная проекция К₁^II определится на фронтальном следе плоскости γ (линия связи). Вторая точка линии пересечения К₂, определится аналогично.

Алгоритм решения задачи:

1.  || П₁

2. h₁(1 Є h₁)=  ∩ γ (2,3) /\  ∩ Σ(ΔABC)

3. К₁ = h₁ ∩ (2,3)

4. β || П₁

5. h₂(5 Є h₂)= β ∩ γ (4,6) /\ β ∩ Σ(ΔABC)

6. К₂ = h₂ ∩ (4,6)

7. (К₁К₂) = γ ∩ Σ(ΔАВС)

Линия пересечения плоскостей, когда одна из них задана следами, а другая плоской фигурой, может быть определе-на и по точкам встречи прямых одной плоскости с дру-гой плоскостью (рис.12).

Для определения точек К₁ и К₂ вводятся две горизон-тальнопроецирующие плоскости  и β. Через сторону тре-угольника АС проводится вспомогательная плоскость . 1^I 2^I - горизонтальная проекция линии пересечения плоскостей  и γ. Точка К₁^II получается при пересечении фронтальной проекции прямой 1^II 2^II с А^IIС^II. Горизон-тальная проекция К₁^I определяется на А^IС^I. Плоскость β проведем через сторону AB. Точка К₂, принадлежащая ли-нии пересечения, определяется аналогично.

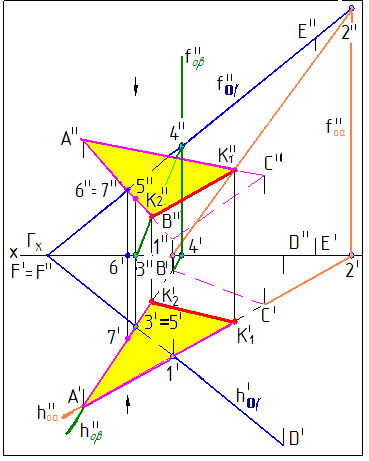
Рис. 12

Алгоритм:

1.  Є (AC) /\  ┴ П₁

2. (1,2)=  ∩ γ

3. К₁ = (1,2) ∩ (A,C)

4. β Є (AB) /\ β ┴ П₁

5. (3,4)= β ∩ γ

6. К₂ = (3,4) ∩ (A,B)

7. (К₁К₂) = γ ∩ Σ(ΔАВС)

На рис. 12 показано определение видимости для данного варианта.

Построение следов линии пересечения плоскостей (рис.10).

Горизонтальным следом М прямой является точка пере-сечения этой прямой с горизонтальной плоскостью проекций, то есть точка, аппликата которой z=0. Для на-хождения горизонтального следа М ≡М^I прямой К₁ К₂ (рис.10) продолжаем фронтальную проекцию прямой до пересечения с осью Х и через эту точку проводим линию проекционной связи до пересечения с горизонтальной про-екцией прямой.

Фронтальным следом N является точка пересечения прямой с фронтальной плоскостью проекций, в этой точ-ке значение у=О. Чтобы определить фронтальный след N≡N^II прямой К₁ К₂ необходимо продлить горизонтальную проекцию этой прямой до пересечения с осью Х и через эту точку провести линию проекционной связи до пересе-чения с фронтальной проекцией прямой.

Построение линии пересечения в аксонометрических проекциях.

В зависимости от номера варианта построение линии пересечения двух плоскостей в аксонометрической проек-ции выполняется в прямоугольной изометрии или в прямо-угольной диметрии. Алгоритм построения линии пересече-ния плоскостей в аксонометрии ничем не отличается от алгоритма решения данной задачи в орто-гональных проекциях. Линия пересечения плоскостей мо-жет быть определена с помощью вспомогательных секу-щих плоскостей или по точкам встречи прямых одной плос-кости с другой. Построения выполняются на одной из вто-ричных проекций и в пространстве

На рис.13 приведен пример определения точки встречи прямой d с плоскостью, заданной треугольником АВС.

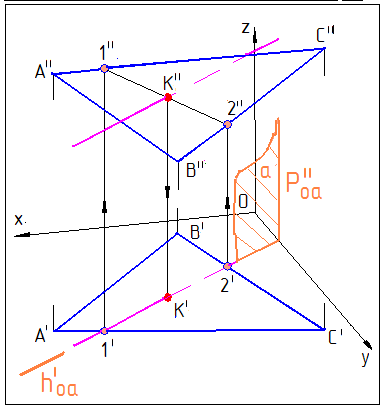
Рис.13

Алгоритм:

1.  Є d /\  ┴ П₁

2. (1,2)=  ∩ Σ(ΔАВС)

3. К₁ = (1,2) ∩ d