1.4 Игра Мариенбад

1.4.1 Правила игры Мариенбад, стратегия выигрыша

Игра Мариенбад – традиционная игра Ним на четыре «кучки» с известным числом предметов в кучках. На немецком водном курорте бювет (место разлива целебной воды) имел 4 яруса. На первом ярусе находился один кран, на втором – 3, на третьем – 5 и на четвертом – 7. Отдыхающие придумали игру: теоретически они перекрывали краны – любое число, но только на одном из ярусов. Побеждал тот, кто закрывал последний кран, рис.1.10.

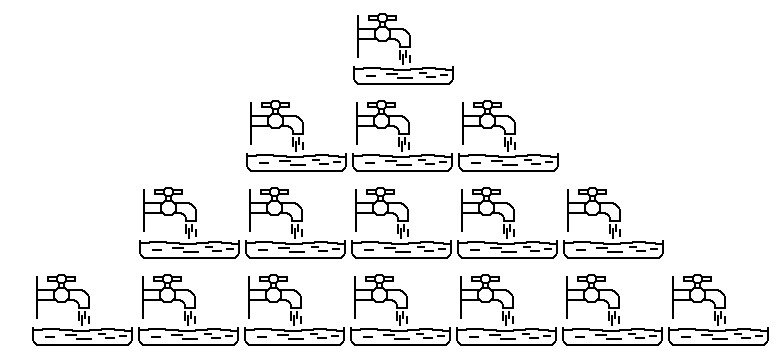
Рисунок 1.10 – Схема бювета водного курорта в Мариенбаде, отключение кранов можно интерпретировать как взятие предметов из кучек в игре Ним

1.4.2 Пример игры в Мариенбад

Алгоритм игры в Мариенбад, как и в игре Ним основывается проверке равенства нулю суммы по модулю 2 двоичных представлений чисел в каждой кучке. Например, для нарисованного бювета

001  011  101  111 = 000.

Очевидно, что мы находимся в точке Гранди и уже проиграли. Предположим, что мы «закроем» 2 крана на 3 уровне – тогда действующими остаются 1, 3, 3 и 7 кранов. Как снова попасть в ядро графа, рис.1.11?

Рассчитываем это так. Временно отбрасываем наибольшую «кучку» (7 кранов) и суммируем остальные по модулю 2:

001  011  011 = 001.

То есть мы попадем в ядро, если во временно отброшенной кучке будет действовать 1 (001) кран. Закрываем 6 кранов на четвертом уровне бювета:

Рисунок 1.11 – Соперники обменялись ходами, комбинация 1-3-3-1 опять точка Гранди, дальнейшая игра легко решается симметричными ходами.

Дальнейшая игра очень проста – мы будем просто симметрично уравнивать кучки предметов: допустим, противник закрыл один кран на втором уровне – закрываем 1 кран на третьем уровне и получаем комбинацию 1-2-2-1, то есть опять сумма по модулю 2 равно 0, игра опять попала в ядро. Рассмотрим последовательность ходов в таблице:

Таблица 1.4

Ход игры в Мариенбад

(число открытых кранов после каждого хода игроков)

Номер хода	Игрок 1				Игрок 2
	Этаж 1	Этаж 2	Этаж 3	Этаж 4	Этаж 1	Этаж 2	Этаж 3	Этаж 4
1	1	3	3	7	1	3	3	1
2	1	2	3	1	1	2	2	1
3	0	2	2	1	0	2	2	0
4	0	1	2	0	0	1	1	0
5	0	0	1	0	Второй игрок победил

(второй пример, когда ходит противник, а игрок выигрывает, с другими ходами, – дописать самим)

2. Постановка задачи на программирование

Задача

Решить задачу о максимальном потоке

Исходные данные:

Граф вводится в графическом диалоге, или путем заполнения матрицы смежности, или чтением матрицы смежности из файла.

Алгоритм:

Определяем степени вершин, если они все четные – у графа есть Эйлеров цикл, если нечетных степеней только 2 – Эйлеров путь.

Вывод:

Сообщение о результат расчетов выводится на экран и/или в текстовый файл.

Примечание:

Один из загружаемых файлов – граф из задания.

Задача 2

Определить, количества деревьев графа с помощью матрицы Трента.

Исходные данные:

Граф вводится в графическом диалоге, или путем заполнения матрицы смежности, или чтением матрицы смежности из файла.

Алгоритм:

Заполняем матрицу Трента: по диагонали степени вершин, в ячейках – количество связей с отрицательным знаком. Считаем один из главных миноров.

Вывод:

Сообщение о результат расчетов выводится на экран и/или в текстовый файл.

Примечание:

Один из загружаемых файлов – граф из задания.

2.2 Описание разработанного объекта

2.2.1 Иерархия наследования

Для работы с графами мною создан собственный класс tgraf, который имеет следующую структуру:

type

tgraf=class

private

fn:integer;

fa:array of array of integer;

fb:array of array of integer;

fc:array of array of integer;

a1:array of array of integer;

a2:array of array of integer;

b1:array of array of integer;

b2:array of array of integer;

fi:integer;

fj:integer;

fk:integer;

procedure seti(const value:integer);

procedure setj(const value:integer);

procedure setk(const value:integer);

procedure setn(const value:integer);

public

property i:integer read fi write seti;

property j:integer read fj write setj;

property k:integer read fk write setk;

function cikl:boolean;

function ejler:boolean;

function fmin:integer;

procedure setab;

procedure setc;

procedure obnul;

procedure setvalue1;

procedure setvalue3;

procedure setvalue2(const value:integer);

property n:integer read fn write setn;

function Getvalue1(ind1,ind2:integer):integer;

function Getvalue2(ind1,ind2:integer):integer;

function Getvalue3(ind1,ind2:integer):integer;

end;

Разработанный класс не имеет в скобках указания на наследование, а значит, наследует по умолчанию от TObject, рис.2.1.

Рисунок 2.1 – Иерархия наследования моего класса.

2.2.2. Организация объекта

Для данного класса реализованы идеи инкапсуляции, включая инкапсуляцию, основанную на разделах private и public. Основное внимание уделено инкапсуляции, основанной на свойствах. Сокрытой частью класса является раздел private, в котором определены:

поле Fn – содержит количество элементов динамически создаваемых массивов (по сути – количество вершин в графах);

поля Fa, Fb, Fc – двумерные динамические массивы целых чисел (указатели на массивы целых чисел) предполагают работу с координатами вершин, ребрами графа;

методы SetI, SetJ, SetK и SetN реализуют инициализацию полей Fi, Fj, Fk и Fn. Правило гласит, что доступ к полям класса должны осуществлять только методы данного класса.

Данное ограничение легко реализуется с помощью механизма свойств, которые описаны в разделе public и являются общедоступными. Наиболее часто применимая конструкция свойств – это отражение чтения данных на поле класса, а запись на метод класса (обычно при записи данных осуществляется дополнительная проверка контроля). Например:

property i:integer read fi write SetI

Методы класса реализуются с помощью процедур и функций. В общедоступном разделе public содержатся следующие методы:

function cikl:boolean; – определение наличия циклов;

function ejler:boolean; – проверка, является ли граф эйлеровым;

function fmin:integer; – минимальная степень графа;

procedure obnul; – обнуление числовых матриц графа.

2.3. Интерфейс программы

Интерфейс программы приведен на рис.2.2.

Рисунок 2.2 – Интерфейс программы, логгирование и входной диалог

Дружественный графический интерфейс моей программы ориентирован на то, чтобы пользователь сразу видел доступные ему функции по созданию графа и расчету числовых характеристик.

Верхнее иконочное меню в основном ориентировано на создание графа. Каждый пункт меню имеет собственный hint-подсказку, а потому на рисунке не прокомментирован. Тем не менее перечислим все выполняемые этими кнопками функции (слева направо):

- очистить поле от нарисованного графа;

- сохранить нарисованный граф для последующей загрузки и расчетов;

- произвести вычисления;

- режим «бездействия» (верхнее меню неактивно);

- создание вершин (щелчок мыши на черном поле, кружки-shape вершин нумеруются автоматически);

- соединение вершин ребрами (щелчок мышью на исходной и конечной вершинах, щелчок на черном поле ни к каким действиям не ведет);

- указание направления дуг (осуществляется двумя щелчками мыши от стартовой к финишной вершинам);

- ввод веса ребер или дуг;

- соединение всех вершин (автоматические получение полносвязного неориентированного графа);

- вызов справки (обращение к собственному hlp-файлу).

Нижний многостраничный компонент после нажатия зеленой стрелки «Вычислить» выводит результаты расчетов. Например, как это показано на рис.2.3.

Рисунок 2.3 – Результаты расчетов в многостраничном компоненте

ЗАКЛЮЧЕНИЕ

В результате проделанной работы выполнено теоретическое обоснование для определения числовых характеристик графа, нумерации его вершин, определения числа циклов, остовного дерева и др.

Разработана программа на языке Object Pascal в среде Delphi 7.0, позволяющая выполнить это в автоматизированном режиме.

Заданный граф находиться как тестовый пример в папке вместе с приложением. Разработанная программа позволяет выполнить аналогичные расчеты и для графов, набранных вручную через интерфейс с использованием мыши и клавиатуры.

Список использованных источников

1. Сигорский В.П. Математический аппарат инженера. – Киев: Техника, 1975. – 768 с.

2. Берж К. Теория графов и ее применения. – М.: Изд-во иностранной литературы, 1962. – 319 с.

3. Кристофидес Н. Теория графов: Алгоритмический подход. – М.: Мир, 1978. – 432 с.

4. Романовский И.В. Дискретный анализ. Учебное пособие для студентов, специализирующихся по прикладной математике и информатике. – СПб.: Невский диалект, 2001. – 240 с.

5. Новиков Ф.А. Дикретная математика для программистов. – СПб.-М.-Харьков: Питер, 2001. – 304 с.

6. Кенту М. Delphi 7 для профессионалов. – М.-СПб.-Харьков: Питер, 204. – 1101 с.

7. Голованов М., Веселов Е. Создание компонентов в среде Delphi. Руководство разработчика. – СПб.: БХВ-Петербург, 2004. – 320 с.