§7.Смешанное произведение

Определение. Смешанным произведением векторов , взятых в указанном порядке, называется число .

Свойства смешанного произведения

1. Критерий компланарности. Для того чтобы три вектора были компланарными, необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.

►Необходимость. Дано: –компланарны. Тогда

{существует плоскость P, что .

Достаточность. Дано: . Рассмотрим два случая:

а);

б)

плоскость

плоскость .◄

2. Геометрический смысл смешанного произведения. Смешанное произведение некомпланарных векторов численно равно объёму V параллелепипеда, построенного на этих векторах, отложенных от одной точки, взятому со знаком плюс, если тройка векторов правая и минус, если левая.

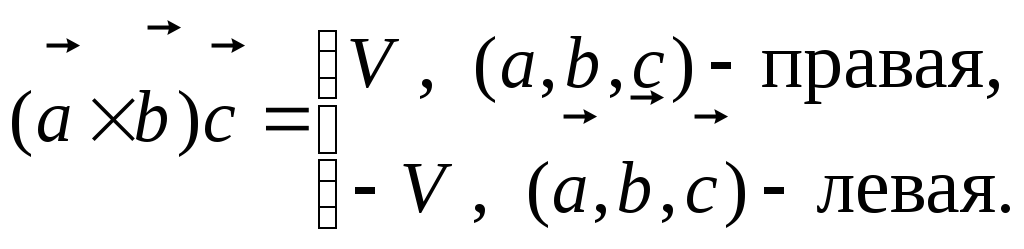(1)

► (см. рис. 1.23). Заметим, что на этом рисунке тройка – левая◄

3 . .

►На основании коммутативности скалярного произведения, достаточно доказать равенство . Если векторы компланарны, то утверждение истинно согласно первому свойству. Если же они некомпланарны, то

(2)

Так как ориентации троек и совпадают, то из (1) и (2) вытекает доказываемое утверждение. ◄

На основании этого свойства мы делаем вывод, что не имеет значения, в каком месте ставить «крестик», а в каком «точку». Поэтому в смешанном произведении эти знаки не ставятся вообще, и оно обозначается так: .

4. : .

►Первые три смешанных произведения равны вследствие того, что тройки одинаково ориентированы, а в последней тройке ориентация меняется, поэтому смешанное произведение меняет знак. ◄

5. : , , .

►Докажем, к примеру, второе равенство:

.◄

6. .

Доказывается так же, как и предыдущее.

Выражение смешанного произведения через координаты перемножаемых векторов в ортонормированном базисе

Пусть заданы три вектора своими координатами в ортонормированном базисе: . Тогда

;

.

Доказательство свойств векторного произведения

Докажем равенство:

. (3)

►Выберем произвольный вектор . Тогда

. (4)

Так как (4) справедливо для любого вектора , то, на основании свойств скалярного произведения, из (4) вытекает (3).

Остальные равенства доказываются аналогично.◄

§ 8. Двойное векторное произведение

Определение. Двойным векторным произведением называется произведение или .

Теорема. Для любых векторов справедливы равенства:

, (1)

.

►Докажем, например, (1). Пусть заданы три произвольных вектора . Построим правый ортонормированный базис следующим образом: в качестве вектора возьмём единичный вектор, коллинеарный , вектор выберем перпендикулярным вектору и так, чтобы были компланарными, и положим . В этом базисе . Тогда ;

; (2)

. (3)

Сравнивая (2) и (3), получаем (1).

Ещё раз подчеркнём, что исходные векторы выбираются произвольным образом, а ортонормированный базис уже подбирается для них. ◄

20