
Контрольная работа 1 семестр
.docВариант № 2
-
Найдите и нарисуйте на координатной плоскости область определения функции
 .
. -
Найдите все частные производные 1-ого порядка для функции
![]() .
.
Найдите
градиент функции z
в точке
F
(2; 1) и производную по направлению вектора
![]() в
этой же точке F.
в
этой же точке F.
-
Постройте линии уровня для функции
 .
. -
Исследуйте на экстремум функцию
 .
. -
Найдите условный экстремум функции
 при
при
 .
. -
Определите какой набор товаров выберет потребитель, обладающий доходом в 300д.ед., если его функция полезности
 ,
а цены единицы товара р1
= 2 д.ед., р2
= 3 д.ед. Напишите уравнения линии
безразличия и нарисуйте три из них при
различных значениях u
.
,
а цены единицы товара р1
= 2 д.ед., р2
= 3 д.ед. Напишите уравнения линии
безразличия и нарисуйте три из них при
различных значениях u
.
Вариант № 3
-
Найдите область определения функции и нарисуйте ее на координатной плоскости
 .
. -
Найдите все частные производные 1-ого порядка для функции
 .
.
Найдите
градиент функции z
в точке
F
(2; 1) и производную по направлению вектора
![]() в
этой же точке F.
в
этой же точке F.
-
Постройте линии уровня для функции
 .
. -
Исследуйте на экстремум функцию
 .
. -
Найдите условный экстремум функции
 при
при
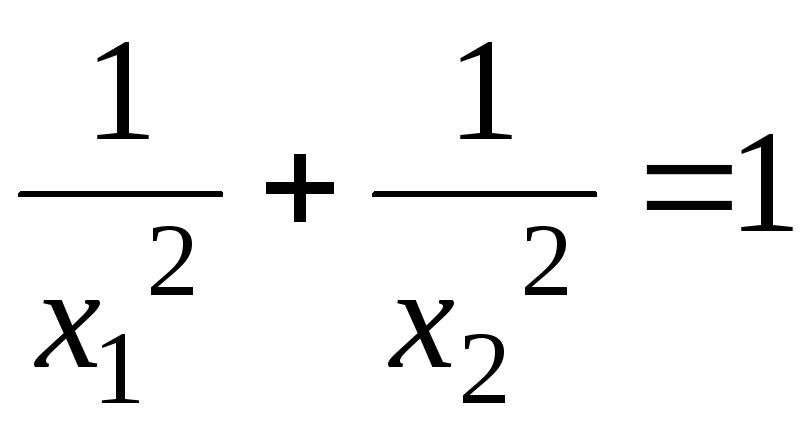 .
. -
Определите какой набор товаров выберет потребитель, обладающий доходом в 300ден.ед., если его функция полезности
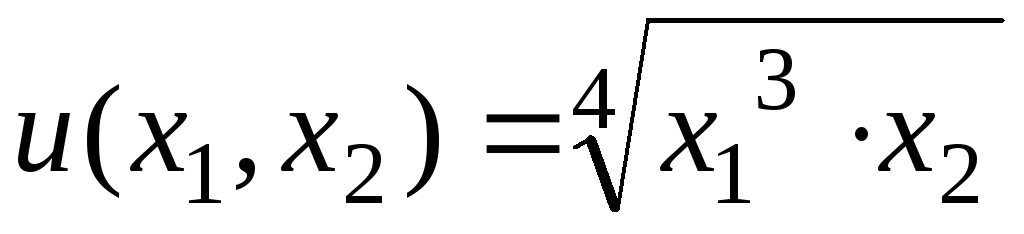 ,
а цены единицы товара р1
= 5 д.ед., р2
= 4 д.ед. Напишите уравнения линии
безразличия и нарисуйте три из них при
различных значениях u
.
,
а цены единицы товара р1
= 5 д.ед., р2
= 4 д.ед. Напишите уравнения линии
безразличия и нарисуйте три из них при
различных значениях u
.
Вариант № 4
-
Найдите область определения функции и нарисуйте ее на координатной плоскости
 .
. -
Найдите все частные производные 1-ого порядка для функции
![]() .
.
Найдите
градиент функции z
в точке
F
(1; 4) и производную по направлению вектора
![]() в
этой же точке F.
в
этой же точке F.
-
Постройте линии уровня для функции
 .
. -
Исследуйте на экстремум функцию
 .
. -
Найдите условный экстремум функции
![]() при
при
![]() .
.
-
Определить какой набор товаров выберет потребитель, обладающий доходом в 200ден.ед., если его функция полезности
 ,
а цены единицы товара р1
= 2 д.ед., р2
= 4д.ед. Напишите уравнения линии
безразличия и нарисуйте три из них
при различных значениях u
.
,
а цены единицы товара р1
= 2 д.ед., р2
= 4д.ед. Напишите уравнения линии
безразличия и нарисуйте три из них
при различных значениях u
.
Вариант 5
-
Найдите область определения функции и нарисуйте ее на координатной плоскости
 .
. -
Найдите все частные производные 1-ого порядка для функции
![]() .
.
Найдите
градиент функции z
в точке
F
(1; 4) и производную по направлению вектора
![]() в
этой же точке F.
в
этой же точке F.
-
Постройте линии уровня для функции
 .
. -
Исследуйте на экстремум функцию
 .
. -
Найдите условный экстремум функции
 при
при
 .
. -
Определить какой набор товаров выберет потребитель, обладающий доходом в 500 ден.ед., если его функция полезности
 ,
а цены единицы товара р1
= 2 д.ед., р2
= 4 д.ед. Напишите уравнения линии
безразличия и нарисуйте три из них при
различных значениях u
.
,
а цены единицы товара р1
= 2 д.ед., р2
= 4 д.ед. Напишите уравнения линии
безразличия и нарисуйте три из них при
различных значениях u
.
Вариант № 6
-
Найдите область определения функции и нарисуйте ее на координатной плоскости
 .
. -
Найдите все частные производные 1-ого порядка для функции
![]() .
.
Найдите
градиент функции z
в точке
F
(1; 4) и производную по направлению вектора
![]() в
этой же точке F.
в
этой же точке F.
-
Постройте линии уровня для функции
 .
. -
Исследуйте на экстремум функцию
 .
. -
Найдите условный экстремум функции
![]() при
при
![]() .
.
-
Определить какой набор товаров выберет потребитель, обладающий доходом в 330ден.ед., если его функция полезности
 ,
а цены единицы товара р1
= 4 д.ед., р2
= 2 д.ед. Напишите уравнения линии
безразличия и нарисуйте три из них
приразличных значениях u
.
,
а цены единицы товара р1
= 4 д.ед., р2
= 2 д.ед. Напишите уравнения линии
безразличия и нарисуйте три из них
приразличных значениях u
.
Вариант № 7
-
Найдите область определения функции и нарисуйте ее на координатной плоскости
 .
. -
Найдите все частные производные 1-ого порядка для функции
![]() .
.
Найдите
градиент функции z
в точке
F
(2; 4) и производную по направлению вектора
![]() в
этой же точке F.
в
этой же точке F.
-
Постройте линии уровня для функции
 .
. -
Исследуйте на экстремум функцию
 .
. -
Найдите условный экстремум функции
![]() при
при
![]() .
.
-
Определить какой набор товаров выберет потребитель, обладающий доходом в 300ден.ед., если его функция полезности имеет вид:
 ,
а цены единицы товара р1
= 2 д.ед., р2
= 4 д.ед. Напишите уравнения линии
безразличия и нарисуйте три из них при
различных значениях u
.
,
а цены единицы товара р1
= 2 д.ед., р2
= 4 д.ед. Напишите уравнения линии
безразличия и нарисуйте три из них при
различных значениях u
.
Вариант № 8
-
Найдите область определения функции и нарисуйте ее на координатной плоскости
 .
. -
Найдите все частные производные 1-ого порядка для функции
![]() .
.
Найдите
градиент функции z
в точке
F
(9; 4) и производную по направлению вектора
![]() в
этой же точке F.
в
этой же точке F.
-
Постройте линии уровня для функции
 .
. -
Исследуйте на экстремум функцию
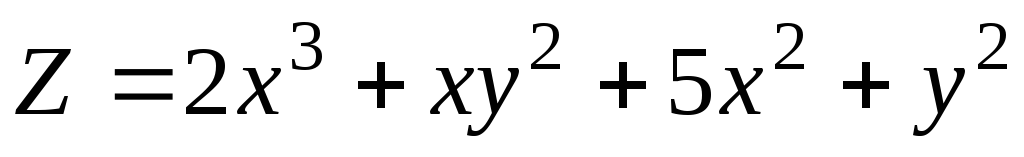
-
Найдите условный экстремум функции
 при
при
 .
. -
Определить какой набор товаров выберет потребитель, обладающий доходом в 500ден.ед., его функция полезности
 ,
а цены единицы товара р1
= 2 д.ед., р2
= 4 д.ед., Напишите уравнения линии
безразличия и нарисуйте три из них при
различных значениях u
.
,
а цены единицы товара р1
= 2 д.ед., р2
= 4 д.ед., Напишите уравнения линии
безразличия и нарисуйте три из них при
различных значениях u
.
Вариант № 9
-
Найдите область определения функции и нарисуйте ее на координатной плоскости
 .
. -
Найдите все частные производные 1-ого порядка для функции
![]() .
.
Найдите
градиент функции z
в точке
F
(1; 2) и производную по направлению вектора
![]() в
этой же точке F.
в
этой же точке F.
-
Постройте линии уровня для функции
 .
. -
Исследуйте на экстремум функцию
 .
. -
Найдите условный экстремум функции
![]() при
при
![]() .
.
-
Функция полезности потребителя имеет вид:
 .
Определить какой набор товаров выберет
потребитель, обладающий доходом в
500 ден.ед., если цены единицы товара
р1
= 2 д.ед., р2
= 4 д.ед.
Напишите
уравнения линии безразличия и нарисуйте
три из них при различных значениях
u..
.
Определить какой набор товаров выберет
потребитель, обладающий доходом в
500 ден.ед., если цены единицы товара
р1
= 2 д.ед., р2
= 4 д.ед.
Напишите
уравнения линии безразличия и нарисуйте
три из них при различных значениях
u..
Вариант № 10
-
Найдите область определения функции и нарисуйте ее на координатной плоскости
 .
. -
Найдите все частные производные 1-ого порядка для функции
![]() .
.
Найдите
градиент функции z
в точке
F
(2; 1) и производную по направлению вектора
![]() в этой же точке F.
в этой же точке F.
-
Постройте линии уровня для функции
 .
. -
Исследуйте на экстремум функцию
 .
. -
Найдите условный экстремум функции
 при
при
 .
. -
Определить какой набор товаров выберет потребитель, обладающий доходом в 300ден.ед., если его функция полезности
 ,
а цены единицы товара р1
= 5 д.ед., р2
= 4 д.ед., Напишите уравнения линии
безразличия и нарисуйте три из них
при различных значениях u
.
,
а цены единицы товара р1
= 5 д.ед., р2
= 4 д.ед., Напишите уравнения линии
безразличия и нарисуйте три из них
при различных значениях u
.
Вариант №11
-
Найдите область определения функции и нарисуйте ее на координатной плоскости
 .
. -
Найдите все частные производные 1-ого порядка для функции
![]() .
.
Найдите
градиент функции z
в точке
F
(2; 0) и производную по направлению вектора
![]() в
этой же точке F.
в
этой же точке F.
-
Постройте линии уровня для функции
 .
. -
Исследуйте на экстремум функцию
 .
. -
Найдите условный экстремум функции
 при
при
 .
. -
Функция полезности потребителя имеет вид:
 .
Найдите функции спроса. Напишите
уравнения линии безразличия и нарисуйте
три из них при различных значениях u
.
.
Найдите функции спроса. Напишите
уравнения линии безразличия и нарисуйте
три из них при различных значениях u
.
Вариант № 12
-
Найдите область определения функции и нарисуйте ее на координатной плоскости
 .
. -
Найдите все частные производные 1-ого порядка для функции
![]() .
.
Найдите
градиент функции z
в точке
F
(2; 1) и производную по направлению вектора
![]() в
этой же точке F.
в
этой же точке F.
-
Постройте линии уровня для функции
 .
. -
Исследуйте на экстремум функцию
 .
. -
Найдите условный экстремум функции
 при
при
 .
. -
Определить какой набор товаров выберет потребитель, обладающий доходом в 400 ден.ед., если его функция полезности
 ,
а цены единицы товара р1
= 2 д.ед., р2
= 4 д.ед. Напишите уравнения линии
безразличия и нарисуйте три из них
при различных значениях u
.
,
а цены единицы товара р1
= 2 д.ед., р2
= 4 д.ед. Напишите уравнения линии
безразличия и нарисуйте три из них
при различных значениях u
.
Вариант № 13
-
Найдите область определения функции и нарисуйте ее на координатной плоскости
 .
. -
Найдите все частные производные 1-ого порядка для функции
![]() .
.
Найдите
градиент функции z
в точке
F
(2; 1) и производную по направлению вектора
![]() в
этой же точке F.
в
этой же точке F.
-
Постройте линии уровня для функции
 .
. -
Исследуйте на экстремум функцию
 .
. -
Найдите точки условного экстремума и условные экстремумы функции
 при условии
при условии
 .
. -
Функция полезности потребителя имеет вид:
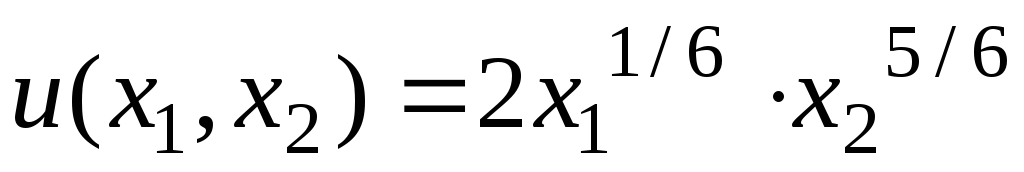 .
Определите какой набор товаров выберет
потребитель, обладающий доходом в 400
ден.ед., если цены единицы товара р1
= 2 д.ед., р2
= 4 д.ед. Напишите уравнения линии
безразличия и нарисуйте три из них при
различных значениях u
.
.
Определите какой набор товаров выберет
потребитель, обладающий доходом в 400
ден.ед., если цены единицы товара р1
= 2 д.ед., р2
= 4 д.ед. Напишите уравнения линии
безразличия и нарисуйте три из них при
различных значениях u
.
Вариант № 14
-
Найдите и нарисуйте на координатной плоскости область определения функции
 .
. -
Найдите все частные производные 1-ого порядка для функции
![]() .
.
Найдите
градиент функции z
в точке
F
(1; 3) и производную по направлению вектора
![]() в
этой же точке F.
в
этой же точке F.
-
Постройте линии уровня для функции
 .
. -
Исследуйте на экстремум функцию
 .
. -
Найдите условный экстремум функции
![]() при
при
![]() .
.
-
Определить какой набор товаров выберет потребитель, обладающий доходом в 300ден.ед., если его функция полезности
 ,
а цены единицы товара р1
= 2 д.ед., р2
= 4 д.ед. Напишите уравнения линии
безразличия и нарисуйте три из них
при различных значениях u
.
,
а цены единицы товара р1
= 2 д.ед., р2
= 4 д.ед. Напишите уравнения линии
безразличия и нарисуйте три из них
при различных значениях u
.
Вариант № 15
-
Найдите область определения функции и нарисуйте ее на координатной плоскости
 .
. -
Найдите все частные производные 1-ого порядка для функции
![]() .
.
Найдите
градиент функции z
в точке
F
(0,5; 1) и производную по направлению
вектора
![]() в
этой же точке F.
в
этой же точке F.
-
Постройте линии уровня для функции
 .
. -
Исследуйте на экстремум функцию
 .
. -
Найдите условный экстремум функции
![]() при
при
![]() .
.
-
Функция полезности потребителя имеет вид:
 .
Определите какой набор товаров выберет
потребитель, обладающий доходом в
400 ден. ед., если цены единицы товара р1
= 2 д.ед., р2
= 4 д.ед. Напишите уравнения линии
безразличия и нарисуйте три из них при
различных значениях u
.
.
Определите какой набор товаров выберет
потребитель, обладающий доходом в
400 ден. ед., если цены единицы товара р1
= 2 д.ед., р2
= 4 д.ед. Напишите уравнения линии
безразличия и нарисуйте три из них при
различных значениях u
.
Вариант № 16
-
Найдите область определения функции и нарисуйте ее на координатной плоскости
 .
. -
Найдите все частные производные 1-ого порядка для функции
![]() .
.
Найдите
градиент функции z
в точке
F
(2; 1) и производную по направлению вектора
![]() в
этой же точке F.
в
этой же точке F.
-
Постройте линии уровня для функции
 .
. -
Исследуйте на экстремум функцию
 .
. -
Найдите условный экстремум функции
 при
при
 .
. -
Определить какой набор товаров выберет потребитель, обладающий доходом в 330ден.ед., если его функция полезности
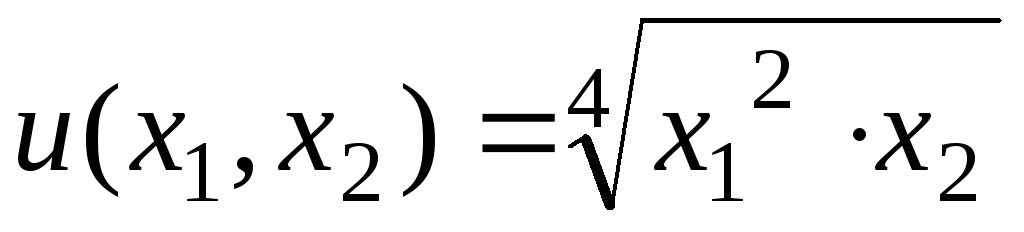 ,
а цены единицы товара р1
= 4 д.ед., р2
= 3 д.ед. Напишите уравнения линии
безразличия и нарисуйте три из них при
различных значениях u
.
,
а цены единицы товара р1
= 4 д.ед., р2
= 3 д.ед. Напишите уравнения линии
безразличия и нарисуйте три из них при
различных значениях u
.
Вариант №17
-
Найдите область определения функции и нарисуйте ее на координатной плоскости
 .
. -
Найдите все частные производные 1-ого порядка для функции
![]() .
.
Найдите
градиент функции z
в точке
F
(2; 1) и производную по направлению вектора
![]() в этой же точке F.
в этой же точке F.
-
Постройте линии уровня для функции
 .
. -
Исследуйте на экстремум функцию
 .
. -
Найдите условный экстремум функции
![]() при
при
![]() .
.
-
Определите какой набор товаров выберет потребитель, обладающий доходом в 300д.ед., если его функция полезности
 ,
а цены единицы товара р1
= 2 д.ед., р2
= 4 д.ед. Напишите уравнения линии
безразличия и нарисуйте три из них при
различных значениях u
.
,
а цены единицы товара р1
= 2 д.ед., р2
= 4 д.ед. Напишите уравнения линии
безразличия и нарисуйте три из них при
различных значениях u
.
Вариант № 18
-
Найдите область определения функции и нарисуйте ее на координатной плоскости
 .
. -
Найдите все частные производные 1-ого порядка для функции
![]() .
.
Найдите
градиент функции z
в точке
F
(2; 1) и производную по направлению вектора
![]() в
этой же точке F.
в
этой же точке F.
-
Постройте линии уровня для функции
 .
. -
Исследуйте на экстремум функцию
 .
. -
Найдите условный экстремум функции
 при
при
 .
. -
Определите какой набор товаров выберет потребитель, обладающий доходом в 300д.ед., если его функция полезности
 ,
а цены единицы товара р1
= 2 д.ед., р2
= 3 д.ед. Напишите уравнения линии
безразличия и нарисуйте три из них при
различных значениях u
.
,
а цены единицы товара р1
= 2 д.ед., р2
= 3 д.ед. Напишите уравнения линии
безразличия и нарисуйте три из них при
различных значениях u
.
Вариант №19
-
Найдите область определения функции и нарисуйте ее на координатной плоскости
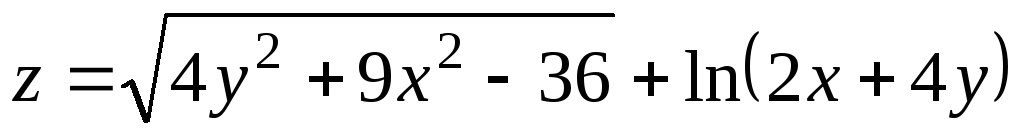 .
. -
Найдите все частные производные 1-ого порядка для функции
![]() .
.
Найдите
градиент функции z
в точке
F
(2; 1) и производную по направлению вектора
![]() в этой же точке F.
в этой же точке F.
-
Постройте линии уровня для функции
 .
. -
Исследуйте на экстремум функцию
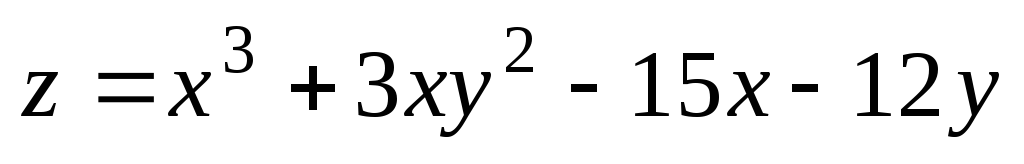 .
. -
Найдите условный экстремум функции
 при
при
 .
. -
Определите какой набор товаров выберет потребитель, обладающий доходом в 300ден.ед., если его функция полезности
 ,
а цены единицы товара р1
= 5 д.ед., р2
= 4 д.ед. Напишите уравнения линии
безразличия и нарисуйте три из них при
различных значениях u
.
,
а цены единицы товара р1
= 5 д.ед., р2
= 4 д.ед. Напишите уравнения линии
безразличия и нарисуйте три из них при
различных значениях u
.
Вариант № 20
-
Найдите область определения функции и нарисуйте ее на координатной плоскости
 .
. -
Найдите все частные производные 1-ого порядка для функции
 .
.
Найдите
градиент функции z
в точке
F
(1; 4) и производную по направлению вектора
![]() в
этой же точке F.
в
этой же точке F.
-
Постройте линии уровня для функции
 .
. -
Исследуйте на экстремум функцию
 .
. -
Найдите условный экстремум функции
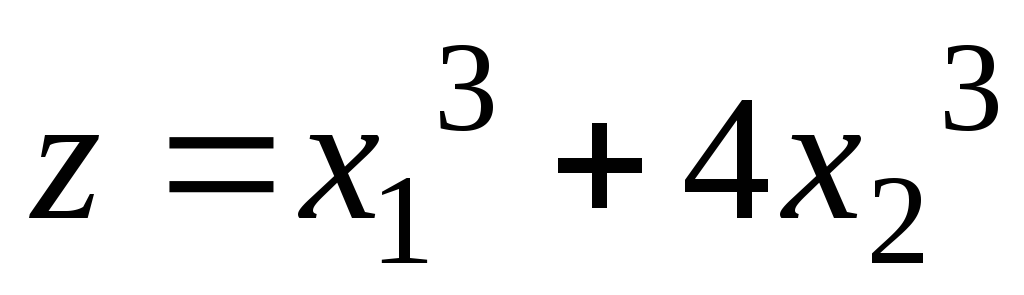 при
при
 .
. -
Определить какой набор товаров выберет потребитель, обладающий доходом в 200ден.ед., если его функция полезности
 ,
а цены единицы товара р1
= 2 д.ед., р2
= 4д.ед. Напишите уравнения линии
безразличия и нарисуйте три из них при
различных значениях u
.
,
а цены единицы товара р1
= 2 д.ед., р2
= 4д.ед. Напишите уравнения линии
безразличия и нарисуйте три из них при
различных значениях u
.
-
Контрольная работа по теме 3, 1-й семестр
Вариант № 1
1.![]() ;
2.
;
2.![]() ;
;
3.![]() ;
4.
;
4.
![]() ;
5.
;
5.
![]() ;
;
6.
![]() ;
7.
;
7.
![]() ;
8.
;
8.
![]() ;
;
9. Вычислите площадь фигуры, ограниченной линиями (сделав рисунок): y = 2x2, y = 2x;
10. Вычислите площадь фигуры, ограниченной линиями (сделав рисунок): y = x2 2х, y = 6 х;
11.
Вычислите объем тела, образованного
вращением вокруг оси ОХ
фигуры, ограниченной линиями (сделав
рисунок):
![]() ;
х
= 4; у
= 0;
;
х
= 4; у
= 0;
12.
![]() ;
13.
;
13.
![]() ;
14.
;
14.
![]() .
.
